Gaussian period
|
Read other articles:
Munisipalitas di Ceará, Brasil Berikut ini adalah daftar dari munisipalitas negara bagian di Ceará (CE), Brasil. Mesoregion Microregion Munisipalitas Centro-Sul Cearense Iguatu Cedro Icó Iguatu Orós Quixelô Lavras da Mangabeira Baixio Ipaumirim Lavras da Mangabeira Umari Varzea Alegre Antonina do Norte Cariús Jucás Tarrafas Várzea Alegre Jaguaribe Baixo Jaguaribe Alto Santo Ibicuitinga Jaguaruana Limoeiro do Norte Morada Nova Palhano Quixeré Russas São João do Jaguaribe Tabuleiro d...

العلاقات البرازيلية السورينامية البرازيل سورينام البرازيل سورينام بدأت في نوفمبر 1975 تعديل مصدري - تعديل العلاقات البرازيلية السورينامية هي العلاقات الثنائية التي تجمع بين البرازيل وسورينام.[1][2][3][4][5] مقارنة بين البلدين هذه مقارن...

Northern region of Michigan's lower peninsula This article is about the region of Michigan's Lower Peninsula. For the northernmost peninsula of Michigan, see Upper Peninsula of Michigan. For the university in the Upper Peninsula, see Northern Michigan University. For the university's athletic program, see Northern Michigan Wildcats. Lower Peninsula of Michigan in the United StatesNorthern Michigan Northern Lower MichiganLower Peninsula of MichiganNorthern Michigan is highlighted in light gree...

US elections 2016 Vermont Republican presidential primary ← 2012 March 1, 2016 (2016-03-01) 2020 → ← VAKS →16 pledged delegates to the 2016 Republican National Convention Candidate Donald Trump John Kasich Home state New York Ohio Delegate count 8 8 Popular vote 19,974 18,534 Percentage 32.34% 30.01% Candidate Marco Rubio Ted Cruz Home state Florida Texas Delegate count 0 0 Popular vote 11,7...
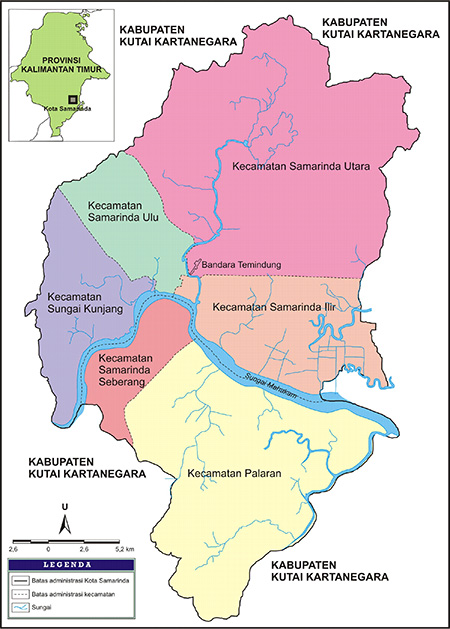
Ada 27 sungai alam yang mengalir di dalam Kota Samarinda dan tersebar di beberapa Kecamatan dan Kelurahan. 27 sungaiyang terbentuk secara alami yang ada di Samarinda itu kemudian dibuatkan Surat Keputusan Walikota Samarinda tentang Penetapan Sungai Sungai alam dalam wilayah Kota Samarinda tahun 2004, yang ditanda tangani Walikota Samarinda H. Achmad Amins Berikut ini adalah daftar sungai alam yang mengalir di KotaSamarinda Kalimantan Timur. ..[1][2] Daftar Sungai Alam di Samar...

Перуанский анчоус Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеГруппа:Костные рыбыКласс:Лучепёрые рыбыПодкласс:Новопёрые �...

Cet article est une ébauche concernant une compétition de football et l’Angleterre. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Coupe d'Angleterre 2006-2007 Généralités Sport Football Organisateur(s) Fédération d'Angleterre de football Éditions 126e Lieu(x) Angleterre Pays de Galles Site(s) Finale au Wembley Stadium Site web officiel TheFACup.com Palmarès Tenant du titre Liverpool FC (7) Vainqueur...

拉米兹·阿利雅Ramiz Alia第1任阿尔巴尼亚總統任期1991年4月30日—1992年4月9日继任萨利·贝里沙阿尔巴尼亚人民议会主席团主席任期1982年11月22日—1991年4月30日前任哈奇·列希继任转任总统阿尔巴尼亚劳动党第一书记任期1985年4月13日—1991年5月4日前任恩维尔·霍查继任无(政党解散) 个人资料出生(1925-10-18)1925年10月18日 阿尔巴尼亚斯库台逝世2011年10月17日(2011歲—10—17)(85�...

Institutional corruption in the United States of America Political corruption Forms and concepts Bribery Cronyism Economics of corruption Electoral fraud Elite capture Influence peddling Kleptocracy Mafia state Nepotism Pyrrhic defeat theory Slush fund Simony State capture State-corporate crime Throffer Anti-corruption International Anti-Corruption Court Group of States Against Corruption International Anti-Corruption Academy International Anti-Corruption Day United Nations Convention against...

جزء من سلسلة عنالحرب الأهلية السوريةعملية السلام السورية السجل التاريخيخطط السلام للجامعة العربية في سوريا2011بعثة المراقبين العرب إلى سوريا2011-12الانخراط الروسي في الحرب الأهلية السورية2012خطة سلام كوفي أنان لسوريا مؤتمر جنيف 2 للسلام في سوريا2012خطة الأخضر الإبراهيمي للسلا�...

الخيارمعلومات عامةصنف فرعي من عقد اشتقاقي جانب من جوانب إدارة المخاطر المالية ممثلة بـ strike price (en) share price at maturity (en) option maturity (en) يستخدمه option trading (en) تعديل - تعديل مصدري - تعديل ويكي بيانات سوق مالية سوق تداول - سند ضمان سوق السندات تقييم السندات [لغات أخرى] سندات الشركة ...

حسان اگزار چنانی معلومات شخصية مكان الميلاد قرية الخويس من أعمال ناحية شاوور بیت رشگ/ مدينة الشوش تاريخ الوفاة سنة 2010 سبب الوفاة نوبة قلبية الجنسية أهواز، إيراني الاسم المستعار حسان اگزار – اگزار – فنان الربابة الحياة العملية المهنة موسيقي، ملحن، مغني عازف/مادح ا�...

British Lions & Wales international rugby union player For other people of the same name, see Josh Adams. Rugby playerJosh AdamsAdams representing Wales during the Six Nations ChampionshipFull nameJoshua Huw AdamsDate of birth (1995-04-21) 21 April 1995 (age 29)Place of birthSwansea, WalesHeight1.83 m (6 ft 0 in)Weight95 kg (209 lb; 14 st 13 lb)SchoolYsgol y StradeRugby union careerPosition(s) Wing, Fullback, CentreCurrent team CardiffSenior careerY...

American actor Chi McBrideMcBride in 2009BornKenneth McBride (1961-09-23) September 23, 1961 (age 62)Chicago, Illinois, U.S.OccupationActorYears active1992–presentSpouseJulissa Marquez Kenneth Chi McBride (/ʃaɪ/ SHY; born September 23, 1961)[1] is an American actor. He has appeared in films, where he is known primarily as a character actor, and in television, where he has had numerous starring roles. In film, he has played prominent roles including The Frighteners (1...
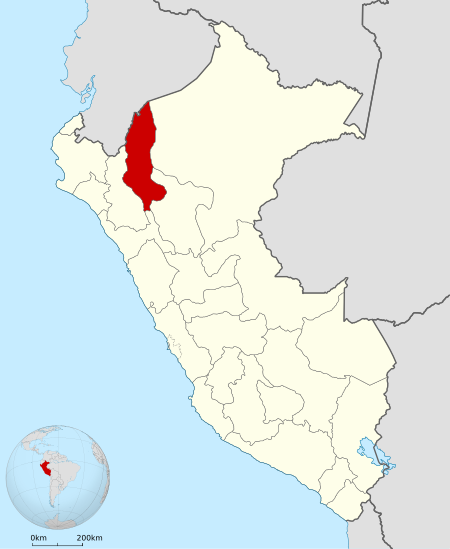
Artikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipedia.Bantulah untuk mengembangkan artikel ini. Jika tidak dikembangkan, artikel ini akan dihapus. Region Amazonas Lokasi Region Amazonas di Peru See other Peruvian regions Presiden Miguel C. Reyes Ibu kota Chachapoyas - Coordinates 6°13′S 77°51′W / 6.22°S 77.85°W / -6.22; -77.85 Wilayah 39.249,13 km² Populasi (per perkiraan tahun 2004) Populasi - Total - Kepadata...

Bad Bad BadAlbum studio karya Superman Is DeadDirilis1 Juli 2002DirekamPregina Studio Sanur BaliLabelSony BMGProduserBobby Kool, Eka Rock, JerinkKronologi Superman Is Dead Superman Is Dead (1998)Superman Is Dead1998 Bad Bad Bad (2002) Kuta Rock City (2003)Kuta Rock City2003 Bad Bad Bad adalah sebuah album musik utama karya Superman Is Dead. Dirilis pada pertengahan tahun 2002. Daftar lagu Long Way To The Bar Tv Brain Bad Bad Bad Beyond This Honesty My Girlfriend Is Pregnant White Town Art...

مقاطعة طارنت علم شعار الإحداثيات 40°28′00″N 17°14′00″E / 40.466666666667°N 17.233333333333°E / 40.466666666667; 17.233333333333 [1] تقسيم إداري البلد إيطاليا[2][3] التقسيم الأعلى بولية العاصمة طارنت التقسيمات الإدارية أفيتراناكاروسينوكاستلانيتاكريسبي�...

Russian politician (born 1964) In this name that follows Eastern Slavic naming customs, the patronymic is Azizboevich and the family name is Azimov. Rakhim AzimovРахим АзимовMember of the State Duma for Kirov OblastIncumbentAssumed office 5 October 2016Preceded byconstituency re-establishedConstituency Kirov (No. 105)Member of the Legislative Assembly of the Kirov OblastIn office13 September 2015 – 18 September 2016Russian Federation Senatorfrom the Komi Republic...

Not to be confused with Eli and Edythe Broad Art Museum. MSU MuseumMSU Museum Main EntranceLocation within MichiganShow map of MichiganMSU Museum (the United States)Show map of the United StatesEstablished1857 (1857)LocationMichigan State University, East Lansing, MI, USCoordinates42°43′53″N 84°28′54″W / 42.7315°N 84.4816°W / 42.7315; -84.4816AccreditationAmerican Alliance of MuseumsDirectorDevon AkmonCuratorJulian C. ChamblissC. Kurt DewhurstMichael ...

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (December 2014) (Learn how and when to remove this message) Trans march with banner reading Collective feminist revolutionaries against all hetrocissexist and racist violence from Paris, 2017 Gendered racism is a form of oppression that occurs due to race and gender. It is perpetuated due to the prevalence of per...









![{\displaystyle P={\begin{cases}{\frac {-1+{\sqrt {p}}}{2}},&{\text{if }}p=4m+1,\\[6pt]{\frac {-1+i{\sqrt {p}}}{2}},&{\text{if }}p=4m+3.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4796d4d2a6c0fd2e1a9c116e1a5fd8e4f5cd5f8)






