Coherent set of characters

In mathematical representation theory, coherence is a property of sets of characters that allows one to extend an isometry from the degree-zero subspace of a space of characters to the whole space. The general notion of coherence was developed by Feit (1960, 1962), as a generalization of the proof by Frobenius of the existence of a Frobenius kernel of a Frobenius group and of the work of Brauer and Suzuki on exceptional characters. Feit & Thompson (1963, Chapter 3) developed coherence further in the proof of the Feit–Thompson theorem that all groups of odd order are solvable.

Definition

Suppose that H is a subgroup of a finite group G, and S a set of irreducible characters of H. Write I(S) for the set of integral linear combinations of S, and I0(S) for the subset of degree 0 elements of I(S). Suppose that τ is an isometry from I0(S) to the degree 0 virtual characters of G. Then τ is called coherent if it can be extended to an isometry from I(S) to characters of G and I0(S) is non-zero. Although strictly speaking coherence is really a property of the isometry τ, it is common to say that the set S is coherent instead of saying that τ is coherent.

Feit's theorem

Feit proved several theorems giving conditions under which a set of characters is coherent. A typical one is as follows. Suppose that H is a subgroup of a group G with normalizer N, such that N is a Frobenius group with kernel H, and let S be the irreducible characters of N that do not have H in their kernel. Suppose that τ is a linear isometry from I0(S) into the degree 0 characters of G. Then τ is coherent unless

  • either H is an elementary abelian group and N/H acts simply transitively on its non-identity elements (in which case I0(S) is zero)
  • or H is a non-abelian p-group for some prime p whose abelianization has order at most 4|N/H|2+1.

Examples

If G is the simple group SL2(F2n) for n>1 and H is a Sylow 2-subgroup, with τ induction, then coherence fails for the first reason: H is elementary abelian and N/H has order 2n–1 and acts simply transitively on it.

If G is the simple Suzuki group of order (2n–1) 22n( 22n+1) with n odd and n>1 and H is the Sylow 2-subgroup and τ is induction, then coherence fails for the second reason. The abelianization of H has order 2n, while the group N/H has order 2n–1.

Examples

In the proof of the Frobenius theory about the existence of a kernel of a Frobenius group G where the subgroup H is the subgroup fixing a point and S is the set of all irreducible characters of H, the isometry τ on I0(S) is just induction, although its extension to I(S) is not induction.

Similarly in the theory of exceptional characters the isometry τ is again induction.

In more complicated cases the isometry τ is no longer induction. For example, in the Feit–Thompson theorem the isometry τ is the Dade isometry.

References

Read other articles:

Chennai Monorail

Rapid transit system in the city of Chennai, India Chennai MonorailOverviewNative nameசென்னை மோனோரெயில்LocaleChennai, Tamil NaduTransit typestraddle-beam MonorailNumber of lines3 (Phase I)HeadquartersChennaiOperationOperation will start2018 (Estd. But later plan was cancelled and Chennai metro was constructed)Train length4 coachesHeadway3 minutesTechnicalSystem length57 km (Phase I)Electrification750 V DCAverage speed65 km/h (40 mph)Top speed80&#...

 

Kabel MIMS

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Kabel MIMS adalah penghantar listrik berinti tembaga dengan isolasi berbahan bubuk yang tebal atau keras. Jenis kabel ini digunakan secara umum di industri. Bahan pembuatan bubuk adalah magnesium oksida. Jumlah inti tembaga dapat berinti tunggal maupun...

 

Google Pay (aplikasi seluler)

Plex (Google) beralih ke halaman ini, yang bukan mengenai Googleplex. Google PayTipeperangkat lunak Versi pertama18 November 2020; 3 tahun lalu (2020-11-18)LisensiProprieterInformasi tambahanSitus webpay.google.com Sunting di Wikidata • L • B • Bantuan penggunaan templat ini Google Pay (juga dikenal sebagai GPay) adalah sebuah aplikasi pembayaran seluler yang dikembangkan oleh Google. Aplikasi ini telah diluncurkan di India, Singapura, dan Amerika Serikat. Sejarah Pa...

Battle of Cobleskill

American Revolutionary War raid Battle of CobleskillPart of the American Revolutionary WarMap detail showing the western frontier of New York. Cobleskill and Cherry Valley are marked in red, Unadilla and Onaquaga (spelled Oghwaga on the map) are marked in blue.DateMay 30, 1778[1]LocationCobleskill, New York42°40′45″N 74°29′8″W / 42.67917°N 74.48556°W / 42.67917; -74.48556Result British victoryBelligerents  Great BritainIroquois  United Sta...

 

Rooting for You (Alessia Cara song)

2019 single by Alessia CaraRooting for YouSingle by Alessia Carafrom the EP This Summer ReleasedAugust 9, 2019 (2019-08-09)Length2:56LabelDef JamSongwriter(s)Alessia CaraccioloJon LevineProducer(s)Jon LevineMidi JonesAlessia Cara singles chronology Ready (2019) Rooting for You (2019) Another Place (2019) Rooting for You is a song recorded by Canadian singer and songwriter Alessia Cara. It was released on August 9, 2019, as the second single from her 2019 EP This Summer.[1&#...

 

إريك جيروم ديكي

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (مايو 2021) إريك جيروم ديكي (بالإنجليزية: Eric Jerome Dickey)‏   إريك جيروم ديكي سنة 2014    معلومات شخصية الميلاد 7 يوليو 1961 [1]  ممفيس[2]  الوفاة 3 يناير 2021 (59 سن�...

Ираклеониты

Ираклеониты — ученики гностика Ираклеона (II век). Упоминаются как особая секта Епифанием и Августином; при крещении и миропомазании они соблюдали обряд помазания елеем и при этом произносили воззвания на арамейском языке, которые должны были освободить душу от власт�...

 

Großer Priel

Großer PrielPemandangan Großer Priel dari HinterstoderTitik tertinggiKetinggian2.515 m (8.251 ft)[1]Puncak1.703 m (5.587 ft)Peringkat ke-25 di AlpenMasuk dalam daftarUltraKoordinat47°43′01″N 14°03′48″E / 47.71694°N 14.06333°E / 47.71694; 14.06333Koordinat: 47°43′01″N 14°03′48″E / 47.71694°N 14.06333°E / 47.71694; 14.06333 [1]GeografiLetakDistrik Gmunden, Austria HuluAustriaPegun...

 

Fool to Cry

1976 single by The Rolling StonesFool to CrySingle by The Rolling Stonesfrom the album Black and Blue B-side Crazy Mama (UK) Hot Stuff (US) Released16 April 1976[1]StudioMusicland, Munich, GermanyGenreSoul[2]Length4:08 (single edit)5:04 (album version)LabelRolling StonesSongwriter(s)Jagger/RichardsProducer(s)The Glimmer TwinsThe Rolling Stones singles chronology Ain't Too Proud to Beg (1974) Fool to Cry (1976) Hot Stuff (1976) Official videoFool to Cry on YouTube Fool to Cry ...

John Stuart Mill

British philosopher and political economist (1806–1873) Stuart Mill redirects here. For the town in Australia, see Stuart Mill, Victoria. John Stuart Mill1873 portrait by George Frederic WattsMember of Parliamentfor City of WestminsterIn office25 July 1865 – 17 November 1868Serving with Robert GrosvenorPreceded byDe Lacy EvansSucceeded byWilliam Henry Smith Personal detailsBorn(1806-05-20)20 May 1806Pentonville, Middlesex, EnglandDied8 May 1873(1873-05-08) (aged 66)A...

 

Antihaitianismo

Prejudice or social discrimination against Haitians in the Dominican Republic This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (March 2022) Part of a series onDiscrimination Forms Institutional Structural Statistical Taste-based Attributes Age Caste Class Dialect Disability Genetic Hair texture Height Language Looks Mental disorder Race / E...

 

Antonis Mor

Anthonis MorAnthonis MorLahirAnthonis Mor1517Utrecht, BelandaMeninggal1577 (umur 60)AntwerpenKebangsaanBelandaDikenal atasLukisanGerakan politikPuncak Renaisans Sir Anthonis Mor, juga dikenal dengan nama Anthonis Mor van Dashorst dan Antonio Moro (sekitar 1517 – 1577), adalah seorang pelukis potret Belanda. Ia pernah melukis untuk istana Inggris, Portugal, dan Spanyol. Ia juga dikenal dengan julukan Antoon, Anthonius, Anthonis atau Mor van Dashorst, dan sebagai Antonio Moro, Anthony More, ...

Abdul Fattah al-Burhan

Abdul Fattah al-Burhanعبد الفتاح البرهانAbdul Fattah al-Burhan pada 2019 Ketua Dewan KedaulatanPetahanaMulai menjabat 21 Agustus 2019Perdana MenteriAbdalla HamdokWakilMohamed Hamdan Dagalo[1]PendahuluPosisi baruPenggantiPetahanaKetua Dewan Militer TransisiMasa jabatan12 April 2019 – 20 Agustus 2019WakilMohamed Hamdan Dagalo[2]PendahuluAhmed Awad Ibn AufPenggantiPosisi dihapuskan Informasi pribadiLahir11 Juli 1960 (umur 63)[butuh rujukan&...

 

Metro (Миннесота)

Metro Описание Страна США Регион Миннесота Город Миннеаполис, Сент-Пол, пригороды Дата открытия июнь 2004 года Компании-перевозчики Metro Transit Годовой пассажиропоток около 6 200 000[1] Сайт metrotransit.org/metro Маршрутная сеть Число маршрутов 7  Медиафайлы на Викискладе Метро (стилиз�...

 

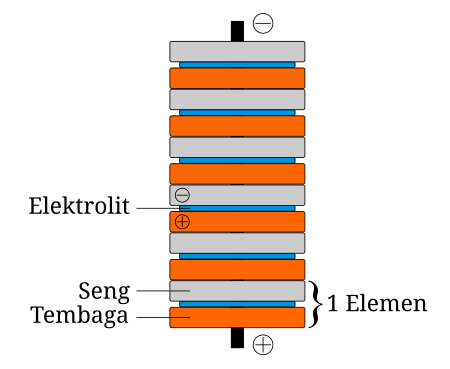
Tumpukan volta

Tumpukan volta dari bahan seng-tembaga. Tumpukan volta adalah rangkaian seri dari beberapa sel galvani.[1] Dalam tumpukan volta, dua jenis logam yang berbeda ditumpuk dan dipisahkan dengan pembatas elektrolit sehingga menghasilkan reaksi elektrokimia.[1] Jika kedua ujung tumpukan volta dihubungkan, arus listrik akan mengalir sehingga menghasilkan fungsi seperti sebuah baterai.[1] Konstruksi Tumpukan volta dideskripsikan oleh Alessandro Volta tahun pada tahun 1800. Sebu...

Template‐ノート:Sign2

このテンプレートは2022年11月21日に削除依頼の審議対象になりました。議論の結果、存続となりました。 このテンプレートについて これはノートで未署名のユーザのページに貼り付けることができます。 この項目のスクリプトを修正してくれる人を修正してくれるとありがたいです。--ナオリン 2006年9月18日 (月) 17:22 (UTC)[返信] すみません、文面から何から書き換えち�...

 

Schießstand

Schießstand aus der Vogelperspektive (Cuxhaven-Altenwalde, 2012) Warnschild: Achtung Schiessbetrieb Ein Schießstand (schweizerisch Schiessstand) bezeichnet eine Schießanlage zum Übungs- und Wettkampfschießen. Er dient zur Durchführung von Sportschießen und wird von der Jägerschaft, Militär, Polizei und anderen Waffenträgern, auch von Privatpersonen, zum Training mit Schusswaffen aller Art genutzt. Schießstände im traditionellen Sinne sind Freigelände (Schießplatz in eigentlichen...

 

William Chambers (architetto)

Questa voce sull'argomento architetti britannici è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Ritratto di William Chambers alla National Gallery of Scotland Sir William Chambers (Gotemburgo, 27 ottobre 1723 – Londra, 17 febbraio 1796) è stato un architetto britannico. Il giardino centrale della Somerset House, realizzata da Chambers a Londra Indice 1 Biografia 2 Note 3 Bibliografia 4 Voci correlate 5 Altri progetti 6 Collegamenti esterni Biograf...

Sotho people

Bantu ethnic group of Southern Africa Ethnic group Sotho peopleBasothoKing Moshoeshoe I, founder of the Southern Basotho Nation of Lesotho, with his Ministers.Total populationc. 7,254,315 (2023 est.)Regions with significant populations South Africa5,103,205 Lesotho2,130,110 Botswana11,000 Eswatini6,000 Namibia4,000LanguagesSesotho & EnglishReligionChristianity, ModimoRelated ethnic groupsPedi people, Tswana people and Lozi people, San people, Phuthi people, Thembu...

 

Perennial philosophy

Idea that all religions share a single truth This article is about the school of thought in philosophy and spirituality. For the popular book on the subject by Aldous Huxley, see The Perennial Philosophy. Part of a series onSpirituality Outline Religion History Timeline Traditional Elite religion Jewish Merkabah Kabbalah Hasidism Christian Catholic Mysticism Sufism Folk religion Modern Buddhist modernism New religious movement Secular spirituality Spiritual but not religious Syncretism Spirit...