BPST instanton
|
Read other articles:

Etelis Etelis carbunculus Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Actinopterygii Ordo: Perciformes Famili: Lutjanidae Subfamili: Etelinae Genus: EtelisG. Cuvier, 1828[1] Spesies tipe Etelis carbunculusG. Cuvier, 1828[1] Spesies[3] Etelis boweni Andrews, Fernandez-Silva, Randall & H.-C. Ho, 2021[2] Etelis carbunculus G. Cuvier, 1828 Etelis coruscans Valenciennes, 1862 Etelis oculatus (Valenciennes, 1828) Etelis radiosus W. D. Anderson, ...

Aivars EndziņšEndziņš (2011)Lahir(1940-12-08)8 Desember 1940Rīga, SSR Latvia, USSR(sekarang Latvia)Meninggal21 November 2023(2023-11-21) (umur 82)AlmamaterUniversitas LatviaPekerjaanPengacara, politikus. Aivars Endziņš (8 Desember 1940 – 21 November 2023) adalah seorang pengacara dan politikus Latvia.[1] Ia lulus dari Universitas Latvia pada tahun 1968 dan pada tahun 1977 memperoleh kandidat gelar ilmu hukum. Pada tahun 1997 menjadi Doktor Ilmu Fikih. Ia p...

Serie C 1957-1958 Competizione Serie C Sport Calcio Edizione 20ª Organizzatore Lega Nazionale Date dal 15 settembre 1957al 25 maggio 1958 Luogo Italia Partecipanti 18 Risultati Vincitore Reggiana(1º titolo) Altre promozioni Vigevano Retrocessioni non previste Statistiche Miglior marcatore Giuseppe Orlando (20) Incontri disputati 306 Gol segnati 725 (2,37 per incontro) Cronologia della competizione 1956-1957 1958-1959 Manuale La Serie C 1957-1958 fu la ventesima ediz...

Demonstrasi air mancur amonia Air mancur amonia adalah sebuah jenis demonstrasi kimia. Eksperimen tersebut dilakukan dengan memasukkan air ke dalam kontainer berisi gas amonia.[1] Amonia larut dalam air dan terjadi tekanan dalam kontainer tersebut. Akibatnya, air menjadi terangkat dan menciptakan efek air mancur. Demonstrasi tersebut memperkenalkan konsep seperti kelarutan dan hukum gas pada tingkat awal. Referensi ^ The Ammonia Smoke Fountain: An Interesting Thermodynamic Adventure M...
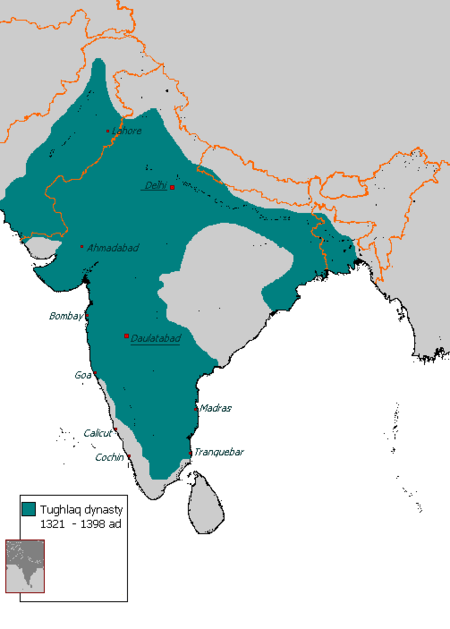
Group of Eastern Indian states For the British company, see East India Company. For other uses, see East India (disambiguation). Not to be confused with East Indies. Place in IndiaEast India Eastern India / The EastCoordinates: 23°15′N 86°00′E / 23.25°N 86.00°E / 23.25; 86.00CountryIndiaStates and territories Andaman and Nicobar Islands Bihar Jharkhand Odisha West Bengal Largest cityKolkataMost populous cities (2011)Bihar: Patna Gaya Bhagalpur Muzaffarpur Purni...

Italian economist and academic, religious sister, and Holy See official Alessandra SmerilliF.M.A.TitlePhDPersonalBorn (1974-11-14) 14 November 1974 (age 49)Vasto, ItalyReligionCatholicNationalityItalianAlma materRoma Tre University, University of East Anglia, Pontifical Faculty of Educational Sciences AuxiliumProfessionEconomist, Secretary of the Dicastery for Promoting Integral Human DevelopmentOrderSalesian Sisters of Don Bosco F.M.A.Senior postingAwardsOrder of the Star of ItalyP...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The topic of this article may not meet Wikipedia's notability guideline for sports and athletics. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is lik...

Gearing-class destroyer This article's tone or style may not reflect the encyclopedic tone used on Wikipedia. The reason given is: Unencyclopedic tone throughout uncited portions of text See Wikipedia's guide to writing better articles for suggestions. (February 2013) (Learn how and when to remove this template message) USS Hanson underway on 17 August 1966 History United States NameHanson NamesakeRobert M. Hanson BuilderBath Iron Works Laid down7 October 1944 Launched11 March 1945 Sponsored ...

2016 studio album by LeadThe ShowcaseStudio album by LeadReleasedJune 8, 2016Recorded2012-2016GenreHip-hop, pop, R&B, danceLabelPony CanyonCD (PCCA-4403)CD [Limited] (PCCA-4400)CD+DVD (PCCA-4401)CD+Booklet (PCCA-4402)Lead chronology Now or Never(2012) The Showcase(2016) Milestone(2018) Singles from The Showcase StillReleased: December 12, 2012 UpturnReleased: June 19, 2013 Green DaysReleased: September 18, 2013 SakuraReleased: February 26, 2014 Omoide BreakerReleased: September 17...

Nawagunjara Nawagunjara atau Nabagunjara[1] (Dewanagari: नवगुंजर; ,IAST: Navaguṅjara, नवगुंजर) adalah makhluk dalam mitologi Hindu yang terbentuk dari sembilan bagian tubuh makhluk yang berbeda-beda. Makhluk ini menjadi ragam hias yang lazim dalam lukisan bergaya Pata-Chitra, di negara bagian Odisha, India. Menurut keyakinan Hindu, makhluk tersebut dianggap sebagai wujud astral dari Dewa Wisnu, atau Kresna yang diyakini sebagai awatara Wisnu. Ma...

西維珍尼亞 美國联邦州State of West Virginia 州旗州徽綽號:豪华之州地图中高亮部分为西維珍尼亞坐标:37°10'N-40°40'N, 77°40'W-82°40'W国家 美國加入聯邦1863年6月20日(第35个加入联邦)首府(最大城市)查爾斯頓政府 • 州长(英语:List of Governors of {{{Name}}}]]) • 副州长(英语:List of lieutenant governors of {{{Name}}}]])吉姆·賈斯蒂斯(R)米奇·卡邁克爾(...

Long, loose overgarment fastening at the neck For other uses, see Cloak (disambiguation). A young man in an evening cloak, 1823. Cloak, 1580–1600 Victoria and Albert Museum, No. 793-1901 Look up cloak in Wiktionary, the free dictionary. A cloak is a type of loose garment worn over clothing, mostly but not always as outerwear for outdoor wear, serving the same purpose as an overcoat, protecting the wearer from the weather. It may form part of a uniform.[1] People in many different so...

British reality TV show (2013–14) TNA British Boot CampGenreReality televisionStarringSee belowCountry of originUnited KingdomOriginal languageEnglishNo. of seasons2[1]No. of episodes14[1] (as of 7 December 2014)ProductionExecutive producerJeremy Borash[2]Production locationsOrlando, Florida, United States[1]London, United KingdomManchester, United Kingdom[3]Nashville, Tennessee, United States[4]Louisville, Kentucky, United StatesRunning time3...

Anglo-Irish landowner and politician The Right HonourableThe Lord EmlyPCPresident of the Board of HealthIn office9 February 1857 – 24 September 1857MonarchVictoriaPrime MinisterThe Viscount PalmerstonPreceded byHon. William CowperSucceeded byHon. William CowperPaymaster General and Vice-President of the Board of TradeIn office12 March 1866 – 26 June 1866MonarchVictoriaPrime MinisterThe Earl RussellPreceded byGeorge GoschenSucceeded byStephen CaveUnder-Secretary of State ...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Duet – berita · surat kabar · buku · cendekiawan · JSTOR Untuk kegunaan lain, lihat Duet (disambiguasi). Het duo, oleh Hendrick Janszoon ter Brugghen Duet merupakan komposisi atau bagian musik yang untuk...

Каличенко Андрей Владимирович Дата рождения 27 января 1975(1975-01-27) (49 лет) Место рождения Новосибирск Гражданство СССР→ Россия Род деятельности Депутат Государственной Думы VII созыва Образование Сибирская государственная академия путей сообщения Партия Единая...

Group of protists CRuMs Collodictyon pseudopodoa Scientific classification Domain: Eukaryota Clade: Opimoda Clade: Podiata Clade: CRuMsBrown et al. 2018[1] Orders Collodictyonida Rigifilida Mantamonadida Synonyms Crumalia Zmitrovich, Perelygin & Zharikov 2022[2] Varisulca Cavalier-Smith 2013 emend. 2021[3] CRuMs or Crumalia[2] is a proposed clade of microbial eukaryotes, whose name is an acronym of the following constituent groups: i) collodictyonids also k...

هذه المقالة مَكتوبةٌ بطريقةٍ تخالف أسلوب ويكيبيديا، ويبدو أنها تعرض فرضياتٍ علميةٍ مبنيةٍ على مصادرَ أولية فقط. فضلاً، ساهم في تطوير هذه المقالة من خلال إعادة صياغتها وفق أسلوب الكتابة في الموسوعة واستبدال المصادر الثانوية بالمصادر الأولية. ما هي الحضارة الآسيوية؟. (يناي...

Canadian businessman and diplomat The HonourableMaurice Frederick StrongPC, CC, OM, FRSC, FRAICStrong, c. 1971Personal detailsBorn(1929-04-29)April 29, 1929Oak Lake, Manitoba, CanadaDiedNovember 27, 2015(2015-11-27) (aged 86)Ottawa, Ontario, CanadaSpouse(s)Pauline Olivette (m. 1950, div. 1980)Hanne Marstrand (m. 1981, sep. 1989)[1][2]Parent(s)Frederick Milton StrongMary FyfeResidence(s)Crestone, Colorado, U.S. (1972-1989)Lost Lake, On...

此條目需要补充更多来源。 (2015年10月24日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:省長 (加拿大) — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 加拿大 加拿大政府与政治系列条目 王室 君主(歷任名單):查爾斯三世 ...

















