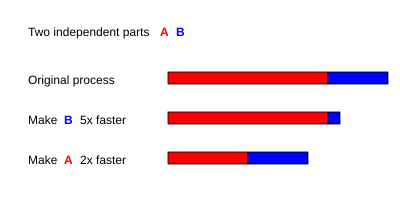
Amdahl's law
|
Read other articles:

Children's book by Laura Numeroff and Felicia Bond This article is about the picture book. For the television adaptation, see If You Give a Mouse a Cookie (TV series). If You Give a Mouse a Cookie AuthorLaura NumeroffIllustratorFelicia BondCountryUnited StatesLanguageEnglishSeriesIf You Give...GenreChildren's literatureMedia typeHardback If You Give a Mouse a Cookie is an American children's picture book written by Laura Numeroff and illustrated by Felicia Bond, first published in 1985 b...

Cet article est une ébauche concernant une chronologie ou une date et le Maroc. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Chronologies Chronologie du Maroc à la Préhistoire Maroc protohistorique : Haut Moyen Âge, Moyen Âge : Chronologie du Haut Moyen Âge Chronologie du Maroc au Moyen Âge Maroc contemporain du XIXe siècle: Maroc contemporain du XXe siècle: La période du Protectorat franç...

Eleições presidenciais portuguesas de 2016 Distritos: Aveiro | Beja | Braga | Bragança | Castelo Branco | Coimbra | Évora | Faro | Guarda | Leiria | Lisboa | Portalegre | Porto | Santarém | Setúbal | Viana do Castelo | Vila Real | Viseu | Açores | Madeira | Estrangeiro ← 2011 • • 2021 → Eleições presidenciais portuguesas de 2016 nos Açores 24 de janeiro de 2016 Demografia eleitoral Hab. inscritos: 228 087 Votantes : 7...

Місто|зображення_підпис= |категорія в Commons= КиселякKiseljak Панорама Киселяка Герб Координати 43°56′35″ пн. ш. 18°04′38″ сх. д.H G O Країна Боснія і Герцеговина Боснія і ГерцеговинаСуб'єкт конфедерації Федерація Боснія і ГерцеговинаКантон СередньобоснійськийМуні�...

Michael Bentt Nombre Michael BenttNacimiento Londres, Inglaterra4 de septiembre de 1964 (59 años)Alma máter Aviation High School, Northampton Community CollegeEstilo OrtodoxoPeso Peso pesadoNacionalidad Estados UnidosEstadísticasTotal 13Victorias 11 • Por nocaut 6Derrotas 2[editar datos en Wikidata] Michael Bentt (Londres, 4 de septiembre de 1964) es un ex boxeador estadounidense. Fue campeón de los pesos pesados de la Organización Mundial de Boxeo entre ...

Het drieluik De Verzoeking van de heilige Antonius is een klein drieluik dat omstreeks 1525 geschilderd is door Jan Wellens de Cock en dat zich bevindt in het Flipje & Streekmuseum in de Nederlandse stad Tiel. Geschiedenis De herkomst van het schilderij is niet bekend. In 1810 kwam het in het bezit van de Sint-Antoniusbroederschap te Tiel. Deze Broederschap bestond al sinds de Middeleeuwen. Op 13 februari van dat jaar werd namelijk: een treffelijk schilderij van de duivelse tentatie van d...

Raedu BashaLahir(1988-06-03)3 Juni 1988Sumenep, IndonesiaKebangsaanIndonesiaNama lainLora Badrus ShalehAlmamaterUniversitas Gadjah MadaPekerjaanSastrawanPenulisAntropologTahun aktif2000 - sekarangSuami/istriIffah HannahAnakElnaz Raedu Basha (lahir 3 Juni 1988) adalah seniman, sastrawan, dan antropolog[1] berkebangsaan Indonesia. Namanya dikenal melalui sejumlah karyanya berupa cerita pendek, puisi, esai sastra dan etnografi yang dipublikasikan media massa, dia juga sering ka...

John LandLand announcing his 2013 campaign for mayorMayor of Apopka, FloridaIn officeJanuary 1, 1971 – April 22, 2014Preceded byLeonard HurstSucceeded byJoe KilsheimerIn officeJanuary 1, 1950 – January 1, 1968Preceded byDr. C. H. DamselSucceeded byLeonard Hurst Personal detailsBorn(1920-11-05)November 5, 1920Plant City, Florida, U.S.DiedNovember 22, 2014(2014-11-22) (aged 94)Orlando, Florida, U.S.Political partyRepublicanSpouseBetty Hall LandProfessionpolitician Joh...

Gayal Status konservasi Domestikasi Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Mamalia Ordo: Artiodactyla Famili: Bovidae Subfamili: Bovinae Genus: Bos Spesies: B. frontalis Nama binomial Bos frontalisLambert, 1804 Gayal (Bos frontalis) atau Mithun adalah sejenis sapi asli timur laut Asia Selatan yang tersebar di Timur laut India, Bangladesh, utara Myanmar, hingga Tiongkok. lbsKeluarga Bovidae yang masih hidupBerikut ini adalah subfamili, genus, dan spesies dalam keluar...

Urraca of Portugal أوراكا البرتغالية (بالبرتغالية: Urraca de Portugal) ملكة ليون القرينة فترة الحكم1165–1175 مرافق yes معلومات شخصية الميلاد 1148قلمرية الوفاة حوالي 1211وامبا، بلد الوليد مكان الدفن دير سانتا ماريا دي وامبا مواطنة مملكة البرتغال الديانة الكاثوليكية الزوج فرناندو الثاني م�...

Karte der Kfz-Kennzeichen in Deutschland (wiedereingeführte Kennzeichen in Blau, nicht wiedereingeführte in Rot) Dies ist eine Liste der deutschen Landkreise und Städte mit ihren Kfz-Kennzeichen. In ihr werden die Verwaltungsbezirke in Deutschland aufgeführt und die dazugehörenden gültigen, aber auch die aufgehobenen Unterscheidungszeichen aufgelistet. Unterscheidungszeichen und Erkennungsnummer Deutsches Kfz-Kennzeichenschild in der gegenwärtigen Form (hinten) Die ein bis drei Buchsta...

Japanese manga series by Masatoshi Kawahara Shura no MonCover of the first tankōbon cover, featuring Mutsu Tsukumo (right)修羅の門(Shura no Mon)GenreMartial arts MangaWritten byMasatoshi KawaharaPublished byKodanshaMagazineMonthly Shōnen MagazineDemographicShōnenOriginal runApril 1987 – November 1996Volumes31 MangaMutsu Enmei-ryū Gaiden: Shura no TokiWritten byMasatoshi KawaharaPublished byKodanshaMagazineMonthly Shōnen MagazineDemographicShōnenOriginal runJuly...

American television series RavenswoodGenre Teen drama Mystery Thriller Supernatural drama Magic realism Horror Created by Joseph Dougherty Oliver Goldstick I. Marlene King Starring Nicole Gale Anderson Tyler Blackburn Steven Cabral Brett Dier Britne Oldford Luke Benward Merritt Patterson Composers Michael Suby Joel J. Richard Country of originUnited StatesOriginal languageEnglishNo. of seasons1No. of episodes10ProductionExecutive producers Leslie Morgenstein I. Marlene King Oliver Goldstick J...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Kalyug Aur Ramayan – news · newspapers · books · scholar · JSTOR (August 2022) (Learn how and when to remove this template message) 1987 Indian filmKalyug Aur RamayanUltra CD CoverDirected byBabubhai MistriStory byManoj Kumar(written by)Dawood Kashmiri (dialogu...

هوغو وولف (بالألمانية: Hugo Wolf) معلومات شخصية اسم الولادة (بالإنجليزية: Hugo Philipp Jacob Wolf) الميلاد 13 مارس 1860(1860-03-13)سلوفينج غرادتس الوفاة 22 فبراير 1903 (42 سنة)فيينا سبب الوفاة احتشاء الدماغ مكان الدفن مقبرة فيينا المركزية مواطنة الإمبراطورية النمساوية المجرية الإمبر�...

Indian caste found predominantly in Maharashtra For Marathi people or Maharashtrians, see Marathi people. MarathaReligionsHinduismLanguagesMarathiKonkaniCountryIndiaPopulated statesMajority:MaharashtraMinority:Goa,Karnataka,Telangana,Madhya PradeshGujaratRegionWestern IndiaCentral India The Maratha caste[note 1] is composed of 96 clans, originally formed in the earlier centuries from the amalgamation of families from the peasant (Kunbi), shepherd (Dhangar), blacksmith (Lohar), carpent...

Palomar knotCategoryHitchReleasingNon-jammingTypical useFishing The Palomar knot (/ˈpæləmɑːr/ PAL-ə-mar) is a knot that is used for securing a fishing line to a fishing lure, snap or swivel. Steps in tying a Palomar knot (free end is colored red). 1. Tie the loose overhand knot. 2. Pass the object through the remaining loop. 3. Start snug. 4. Finish snug (pull evenly on standing ends). 5. View of obverse side. To tie the knot first double 8–12 inches of line into a loop and pass it th...

Outdated grouping of human beings For other uses, see Mongoloid (disambiguation). Mongoloid (/ˈmɒŋ.ɡə.lɔɪd/[1]) is an obsolete racial grouping of various peoples indigenous to large parts of Asia, the Americas, and some regions in Europe and Oceania. The term is derived from a now-disproven theory of biological race.[2] In the past, other terms such as Mongolian race, yellow, Asiatic and Oriental have been used as synonyms. The concept of dividing humankind into the Mon...

Artikel ini bukan mengenai Hari Perdamaian Sedunia. Hari Perdamaian InternasionalBendera Perserikatan Bangsa-BangsaDirayakan olehsemua negara anggota PBBJenisDeklarasi Internasional PBBPerayaanMultiple world wide eventsTanggal21 SeptemberFrekuensitahunanTerkait denganPeace Movement Hari Perdamaian Internasional (bahasa Inggris: International Day of Peace), terkadang secara tidak resmi ada yang menyebutnya Hari Perdamaian Dunia (World Peace Day), diperingati setiap tahun pada tanggal 21 Se...

Amphibians that produce poisonPoison dart frogs are well known for their brightly colored skin. The bright colors warn potential predators of their toxicity. Poisonous amphibians are amphibians that produce toxins to defend themselves from predators. Amphibians Most toxic amphibians are poisonous to touch or eat. These amphibians usually sequester toxins from animals and plants on which they feed, commonly from poisonous insects or poisonous plants. Except certain salamandrid salamanders that...



![{\displaystyle {\begin{cases}S_{\text{latency}}(s)\leq {\dfrac {1}{1-p}}\\[8pt]\lim \limits _{s\to \infty }S_{\text{latency}}(s)={\dfrac {1}{1-p}}.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5704c5d1949dcb3e9f130c974acb3a742e2cf4be)