Alpha–beta transformation
|
Read other articles:

Paus Pius VII (1742-1823) dan Kardinal Giovanni Battista Caprara (1733-1810), yang diangkat menjadi kardinal oleh Paus Pius VI pada 18 Juni 1792. Paus Pius VII (menjabat 1800–1823) mengangkat 99 kardinal dalam 19 konsistori. 11 Agustus 1800 Ercole Consalvi (1757-1824) Diego Innico Caracciolo Ercole Consalvi 20 Oktober 1800 Luis María de Borbón y Vallabriga, 14th Count of Chinchón (1777-1823) Luis María de Borbón y Vallabriga 23 Februari 1801 Bartolomeo Pacca (1756-1844) Giuseppe Firrao...

Fareed ZakariaFareed Zakaria tahun 2013LahirFareed Rafiq Zakaria20 Januari 1964 (umur 60)Mumbai, Maharashtra, IndiaAlmamaterUniversitas Yale (B.A.)Universitas Harvard (Ph.D.)PekerjaanWartawan, penulisKarya terkenalTime, penyunting kontributor (2010–2014)Fareed Zakaria GPS, pembawa acara (2008–sekarang) Newsweek International, penyunting (2000–2010) Foreign Exchange, pembawa acara (2005–2007) Foreign Affairs, mantan penyunting pelaksanaGelarPemerintah India menganugerahi pengharg...

العلاقات التشادية المارشالية تشاد جزر مارشال تشاد جزر مارشال تعديل مصدري - تعديل العلاقات التشادية المارشالية هي العلاقات الثنائية التي تجمع بين تشاد وجزر مارشال.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه الم�...

Pour les articles homonymes, voir Braun et Theo. Ne doit pas être confondu avec Théodore Braun. Cet article est une ébauche concernant un homme politique français. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Théo BraunBiographieNaissance 24 octobre 1920RombasDécès 2 mai 1994 (à 73 ans)MijasNom de naissance Thibaut Joseph BraunNationalité françaiseActivité Homme politiquemodifier - modifier le...

ديربي ميلانو أسماء أخرىديربي الغضب ديربي ديلا مادونيناالموقع إيطاليا (ميلانو)الفرق المتنافسةإيه سي ميلان إنتر ميلانأول لقاءإيه سي ميلان 2–1 إنتر ميلان [1] وديـة (كياسو، سويسرا) (18 أكتوبر 1908)عدد المواجهاتالرسمية: 234 مجموعها: 305الأكثر فوزاالرسمية: إنتر ميلان (86) مجموعها:...

German World War II flying ace (1921–1943) Rudolf MiethigMiethig as a LeutnantBorn(1921-10-17)17 October 1921ZwickauDied10 June 1943(1943-06-10) (aged 21)near Krymskaja Cause of deathKilled in action Allegiance Nazi GermanyService/branch LuftwaffeYears of service1939–43RankHauptmann (captain)UnitJG 52Commands held3./JG 52Battles/warsSee battles World War II Eastern Front Operation Barbarossa Kuban bridgehead † AwardsKnight's Cross of the Iron Cross Rud...

U.S. House district for New York NY-7 redirects here. The term may also refer to New York State Route 7. New York's 7th congressional district From 2023 to 2025 From 2025Interactive map of district boundariesRepresentative Nydia VelázquezD–BrooklynDistribution100% urban0% ruralPopulation (2022)699,930[1]Median householdincome$88,141[2]Ethnicity36.2% White35.3% Hispanic13.2% Asian10.1% Black3.5% Two or more races1.7% otherCook PVID+31[3] New York's 7th congress...

Pour les articles homonymes, voir Pella. Giuseppe Pella Fonctions Président du Conseil des ministres d'Italie 17 août 1953 – 18 janvier 1954(5 mois et 1 jour) Président Luigi Einaudi Prédécesseur Alcide De Gasperi Successeur Amintore Fanfani Ministère des Affaires étrangères 17 août 1953 – 18 janvier 1954(5 mois et 1 jour) Président du Conseil Lui-même Prédécesseur Alcide De Gasperi Successeur Attilio Piccioni 19 mai 1957 – 1er juillet 1958(1 an, 1...

V LiveURLvlive.tvTipeSiaran videoBersifat komersial?YaPendaftaranOpsionalBahasaKorea, Inggris, Thai, Spanyol, Vietnam, Portugis, Indonesia, Tionghoa (Sederhana dan Tradisional), JepangPemilikNaver Corporation (2015-2022) Weverse Company (2022-sekarang)Berdiri sejakAgustus 2015; 8 tahun lalu (2015-08)Service retirement31 Desember 2022 NegaraKorea Selatan V Live (ditulis sebagai VLIVE), kadang-kadang disebut sebagai V App, adalah layanan siaran video langsung asal Korea Selatan yang memung...

Carol by Nikephoros LytrasPart of a series on theCulture of Greece History Ancient regions and tribes Byzantine and Ottoman Greeks Christianization Colonization Coups d'état Demographic (Modern) Economic Geographical name changes Greek countries and regions Greek Muslims Renaissance scholars Hellenic languages and Proto-Greek Inventions and discoveries Language question Military Monarchy (Kings and royal family) Phanariotes Polis Population exchange of 1923 People Languages Mythology Cuisine...
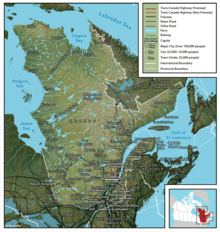
Region of Eastern Canada Not to be confused with Canadian Prairies. PlaceCentral Canada Centre du Canada (French)Map of Central Canada, defined politicallyCoordinates: 50°N 79°W / 50°N 79°W / 50; -79CompositionOntarioQuebecLargest cityTorontoLargest metroGreater Toronto AreaCanadian Confederation1 July 1867Area (2021 - land,[1] 2017 - fresh water[2][3]) • Total2,552,291.51 km2 (985,445.26 sq mi) •&...

Hungarian poet (1773–1805) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Mihály Csokonai – news · newspapers · books · scholar · JSTOR (February 2020) (Learn how and when to remove this message)The native form of this personal name is Csokonai Vitéz Mihály. This article uses Western name order whe...

Gereja Kristen Protestan Pakpak DairiPenggolonganLutheranPemimpinBishop Pdt. Abed Nego Padang Batanghari, M.Th [1] Sekjen Pdt. Jonhson Anakampun S.Th, MMWilayahIndonesiaBahasaBatak Pakpak/DairiDidirikan25 Agustus 1991 Sumatera UtaraTerpisah dariHKBPUmat35.873 jiwaSitus web resmigkppdpusat.org Gereja Kristen Protestan Pakpak Dairi (disingkat GKPPD) adalah kelompok Gereja Kristen Protestan di Indonesia, yang berkantor pusat di Jl. Air Bersih, Complex Centrum GKPPD, kelurahan Sidiangkat,...

نقش النمارةمعلومات عامةالبداية 328 (غريغوري) المكان Room 314 (en) المالك الدولة الفرنسية لغة العمل أو لغة الاسم العربية المواد المستخدمة بازلت المجموعة Department of Near Eastern Antiquities of the Louvre (en) (1903 – ) نظام الكتابة أبجدية نبطية مكان الاكتشاف Namara (en) طريقة التصنيع نقش[1] الطول 173 سنتيمتر&#...

Questa voce o sezione sull'argomento Matematica è priva o carente di note e riferimenti bibliografici puntuali. Sebbene vi siano una bibliografia e/o dei collegamenti esterni, manca la contestualizzazione delle fonti con note a piè di pagina o altri riferimenti precisi che indichino puntualmente la provenienza delle informazioni. Puoi migliorare questa voce citando le fonti più precisamente. Segui i suggerimenti del progetto di riferimento. La teoria della probabilità è lo studio m...

Deaf sign language used in the US Sandy River Valley SignNative toUnited StatesRegionSandy River Valley, MaineEra19th centuryLanguage familyMartha's Vineyard Sign Language?Language codesISO 639-3None (mis)GlottologNone Sandy River Valley Sign Language was a village sign language of the 19th-century Sandy River Valley in Maine. Together with the more famous Martha's Vineyard Sign Language and Henniker Sign Language, it was one of three local languages which formed the basis of American Si...

Israeli chocolate brand Product typeConfectioneryOwnerUnileverCountry IsraelMarketsIsrael, North America, United Kingdom, France, Australia, ArgentinaWebsitehttps://www.unilever.co.il/brands/nutrition/klik/ Klik (Hebrew: קליק) is an Israeli candy brand owned by Unilever Food Solutions, a subsidiary of Unilever. It is used for various chocolate, candy, and chocolate-covered products, including chocolate-covered corn flakes and malted milk balls. Overview Milk and white chocolate pearl...

Yevhen Khacheridi Informasi pribadiNama lengkap Yevhen Hryhorovych KhacheridiTanggal lahir 28 Juli 1987 (umur 37)Tempat lahir Melitopol, Uni SovietTinggi 1,97 m (6 ft 5+1⁄2 in)[1]Posisi bermain BekInformasi klubKlub saat ini FC Dynamo KyivNomor 34Karier junior2007 FC Dynamo-2Karier senior*Tahun Tim Tampil (Gol)2005–2008 Olkom Melitopol 25 (1)2006–2008 → Volyn Lutsk (pinjaman) 24 (2)2008– Dynamo Kyiv 35 (1)Tim nasional‡2009– Ukraina 8 (0) * Penamp...

Allied landing operations in French North Africa during World War II Operation TorchPart of the North African campaign of the Second World WarLandings during the operationDate8–16 November 1942 (1 week and 1 day)LocationFrench Morocco, French AlgeriaResult Allied victoryTerritorialchanges Anglo-American occupation of French Morocco and French Algeria Free French control of French West Africa Case Anton (Axis occupation of southern France)Belligerents United States Unite...
コノート地方Connachta / Cúige ChonnachtConnacht / Connaught 旗 北緯53度46分48秒 西経9度3分0秒 / 北緯53.78000度 西経9.05000度 / 53.78000; -9.05000座標: 北緯53度46分48秒 西経9度3分0秒 / 北緯53.78000度 西経9.05000度 / 53.78000; -9.05000国 アイルランド構成県 ゴールウェイ県リートリム県メイヨー県ロスコモン県スライゴ県政府 • 国会議員数 無所属6名統�...






























