Wagstaff-Primzahl
|
Read other articles:

Komando Distrik Militer 1314/Gorontalo UtaraLambang Resmi Korem 133/Nani WartaboneDibentuk25 Juni 2019Negara IndonesiaAliansiKorem 133/NWBCabangTNI Angkatan DaratTipe unitKodimPeranSatuan TeritorialBagian dariKodam XIII/MerdekaMakodimKwandang, Gorontalo UtaraJulukanKodim 1314/GorutPelindungTentara Nasional IndonesiaMotoSETIA TERJANG(SEmangat Tekad Intensif Akan TERus berJuANG)Baret H I J A U Ulang tahun25 JuniTokohKomandanLetkol Czi. Adityo Bangun PratomoKepala Staf- Komando Di...

Letak Provinsi Barcelona di Spanyol Provinsi Barcelona merupakan sebuah provinsi di Spanyol. Provinsi ini letaknya di bagian timur laut di negara itu. Tepatnya di region Catalunya. Pada tahun 2010, provinsi ini memiliki jumlah penduduk sebesar 5.511.147 jiwa dan memiliki luas wilayah 7.733 km². Provinsi ini memiliki angka kepadatan penduduk 712,68 jiwa/km². Ibu kotanya di Barcelona. Pranala luar Situs web resmi lbsProvinsi di Spanyol Álava/Araba Albacete Alicante/Alacant Almería Astu...

Diprotodontia[1] Periode 28–0 jtyl PreЄ Є O S D C P T J K Pg N Oligosen Akhir - Sekarang Diprotodontia Seekor diprotodon, Walabi Agile (Macropus agilis)TaksonomiKerajaanAnimaliaFilumChordataKelasMammaliaOrdoDiprotodontia Owen, 1866 SubordoVombatiformesPhalangeriformesMacropodiformesDistribusiEndemikAustralasia lbs Diprotodontia (pengucapan bahasa Inggris: [daɪ.proʊ.toʊ.dɑːn.ʃiːə]; Yunani, berarti dua gigi depan) adalah ordo besar dari sekitar 120 mamalia marsupia...

Mesin Pratt & Whitney PW1000G Pratt & Whitney PW1000G adalah sebuah keluarga mesin high-bypass geared turbofan, yang saat ini dipilih sebagai mesin eksklusif untuk Airbus A220, Mitsubishi SpaceJet, dan E-Jets generasi kedua Embraer, dan sebagai opsi pada Irkut MC-21 dan Airbus A320neo. Proyek ini sebelumnya dikenal sebagai Geared Turbofan (GTF), dan awalnya Advanced Technology Fan Integrator (ATFI). Mesin tersebut diharapkan dapat mengurangi penggunaan bahan bakar dan kebisingan di da...

Keadaan transisi (Inggris: transition state) sebuah reaksi kimia merujuk pada konfigurasi tertentu pada koordinat reaksi. Ia didefinisikan sebagai sebuah keadaan yang memiliki energi tertinggi di sepanjang koordinat reaksi. Pada titik ini, dengan berasumsi bahwa reaksi yang sedang berjalan adalah reaksi takreversibel, penabrakan molekul reaktan akan selalu menghasilkan produk.[1] Keadaan transisi yang diperlihatkan di bawah ini terjadi selama reaksi SN2 dari bromoetana dengan anio...
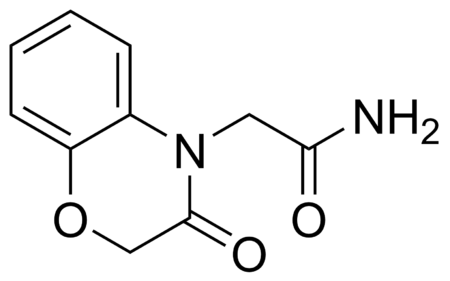
Chemical compound ParaxazoneClinical dataPregnancycategory ? Routes ofadministrationOralATC codenoneLegal statusLegal status In general: uncontrolled Identifiers IUPAC name 2-(3-oxo-2,3-dihydro-4H-1,4-benzoxazin-4-yl)acetamide CAS Number26513-79-1PubChem CID3047812ChemSpider2310126UNII2H6ON8WA7LCompTox Dashboard (EPA)DTXSID10181096 Chemical and physical dataFormulaC10H10N2O3Molar mass206.201 g·mol−13D model (JSmol)Interactive image SMILES O=C(N)CN1c2c(OCC1=O)cccc2 Paraxazone is a...
周處除三害The Pig, The Snake and The Pigeon正式版海報基本资料导演黃精甫监制李烈黃江豐動作指導洪昰顥编剧黃精甫主演阮經天袁富華陳以文王淨李李仁謝瓊煖配乐盧律銘林孝親林思妤保卜摄影王金城剪辑黃精甫林雍益制片商一種態度電影股份有限公司片长134分鐘产地 臺灣语言國語粵語台語上映及发行上映日期 2023年10月6日 (2023-10-06)(台灣) 2023年11月2日 (2023-11-02)(香�...

James RandiJames Randi en 2009.BiographieNaissance 7 août 1928TorontoDécès 20 octobre 2020 (à 92 ans)PlantationNom de naissance Randall James Hamilton ZwingeNationalité Canadien, AméricainFormation École du dimancheActivités Philosophe, écrivain, prestidigitateur, illusionnistePériode d'activité 1946-2015Conjoint Deyvi Orangel Peña Arteaga (d) (de 2013 à 2020)Autres informationsMembre de Mouvement des brightsMouvement AthéismeSite web (en) www.randi.orgDist...

Artikel ini bukan mengenai Ion Television atau implantasi ion. Diagram skematik saluran ion. 1 - domain saluran (biasanya empat domain per saluran), 2 - serambi luar, 3 - filter selektivitas, 4 - diameter filter selektivitas, 5 - situs fosforilasi, 6 - membran sel. Saluran ion adalah protein membran berbentuk pori yang membebaskan ion untuk melintasi pori saluran. Fungsi saluran ion adalah untuk membuat potensial rehat membran, membentuk potensial aksi dan sinyal listrik lainnya oleh pemintua...

لمعانٍ أخرى، طالع دوبريانكا (توضيح). دوبريانكا (بالأوكرانية: Добрянка) تقسيم إداري البلد أوكرانيا [1] خصائص جغرافية إحداثيات 52°03′42″N 31°10′50″E / 52.061666666667°N 31.180555555556°E / 52.061666666667; 31.180555555556 المساحة 14.3 كيلومتر مربع الارتفاع 144 متر السكان ا...

Alternatives to the current banner This is a list comprising flags proposed as alternatives to the current flag of Australia, which have received media coverage. National flags Flag Date Name Designer Description Notes/References 1854 Eureka Flag Lieutenant Henry Ross[1] The battle flag of the Eureka Stockade featured the five stars of the constellation Crux Australis in white on a white cross and blue field. [2][3][4] 1900 Melbourne Evening Herald Flag (Blue) ...

German classical scholar and historian (1817–1903) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Theodor Mommsen – news · newspapers · books · scholar · JSTOR (November 2023) (Learn how and when to remove this message) Theodor MommsenBornChristian Matthias Theodor Mommsen(1817-11-30)30 November 1817Gardi...

För andra betydelser, se Chile (olika betydelser). República de ChileRepubliken Chile Flagga Statsvapen Valspråk: Por la razón o la fuerza (Spanska: Genom förnuft eller styrka) Nationalsång: Himno nacional de Chile läge Huvudstad(även största stad) Santiago de Chile Officiellt språk spanska Demonym chilensk, chilenare[1] Statsskick Republik - President Gabriel Boric - Regeringschef Gabriel Boric Självständighet från Spanien - De...

The Scout Association of the BahamasLocation19 Dolphin Drive P.O. Box N-4272 NassauCountryBahamasFounded1 August 1974 Incorporated 19 November 1975FounderThe Boy Scouts Association of the United KingdomMembership644AffiliationWorld Organization of the Scout Movement Websitescoutbahamas.org Scouting portal Scouting in The Bahamas began in 1912. For the history of Scouting in the Bahamas generally see Scouting in the Bahamas. The Boy Scouts Association of the United Kingdom first registe...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (أبريل 2020) الصفحات الواردة أدناه تحتوي على معلومات حول الأحداث في قرون و آلاف السنين محددة. عنتقرون و ألفيات ألفية قر...

Roger WilliamsPatung Roger WilliamsLahir1603London, InggrisMeninggal1683Providence, Rhode IslandPekerjaanmenteri, pengarang, pengkhotbahSuami/istriMary BarnardAnak6 Roger Williams (circa 1603 – antara Januari dan Maret 1683) adalah teolog Protestan Amerika, dan pendukung kebebasan beragama dan pemisahan gereja dari negara. Pada tahun 1636, ia mendirikan koloni di Rhode Island, yang menyediakan tempat bernaung bagi kaum yang menganut agama minoritas. Ia juga mempelajari bahasa penduduk asli...

Cette page concerne l'année 1845 (MDCCCXLV en chiffres romains) du calendrier grégorien. Pour l'année 1845 av. J.-C., voir 1845 av. J.-C. Chronologies La reine Victoria et le prince Albert reçus au château d'Eu par le roi Louis-Philippe et la reine Marie-Amélie. Peinture de Franz Xaver Winterhalter.Données clés 1842 1843 1844 1845 1846 1847 1848Décennies :1810 1820 1830 1840 1850 1860 1870Siècles :XVIIe XVIIIe XIXe XXe XXIeMillénaires&...

Motorway in Great Britain This article is about the English motorway. For the Dutch motorway, see A38 motorway. A38(M)Aston ExpresswayRoute informationMaintained by Birmingham City CouncilLength2.0 mi (3.2 km)Existed1972–presentHistoryOpened and completed: 1972Major junctionsNorth endGravelly HillMajor intersectionsM6 motorwaySouth endBirmingham city centre LocationCountryUnited KingdomCountiesWest MidlandsPrimarydestinationsBirmingham city centre Road network Roads...

Tasmanian International 1995DoppioSport Tennis Detentoridel titolo Linda Harvey-Wild Chanda Rubin Vincitori Kyōko Nagatsuka Ai Sugiyama Finalisti Manon Bollegraf Larisa Neiland Punteggio2–6, 6–4, 6–2 Tornei Singolare Singolare Doppio Doppio 1994 1996 Voce principale: Tasmanian International 1995. Il doppio del Tasmanian International 1995 è stato un torneo di tennis facente parte del WTA Tour 1995. Linda Harvey-Wild e Chanda Rubin erano le detentrici del titolo, ma hanno partec...

砂の女 Woman in the Dunes 映画キービジュアル(『映画評論』1965年3月号より)監督 勅使河原宏脚本 安部公房原作 安部公房製作 市川喜一、大野忠出演者 岡田英次、岸田今日子音楽 武満徹撮影 瀬川浩編集 守随房子配給 東宝公開 1964年2月15日(全国公開は1964年4月14日) 1964年10月25日上映時間 147分(モノクロ)製作国 日本言語 日本語テンプレートを表示 ポータル 映画 �...





































































































