Vierzehneck
| |||||||||||||||||||
Read other articles:

Emmanuel de Grouchy Emmanuel, marquis de Grouchy (23 Oktober 1766 – 29 Mei 1847) adalah seorang jenderal dan marsekal Prancis. Biografi Grouchy bergabung dengan divisi artileri Prancis pada tahun 1779 dan dipindahkan ke divisi kavaleri pada tahun 1882. Meskipun ia termasuk keluarga bangsawan dan memiliki koneksi dengan istana, tetapi ia bersimpati dengan para pejuang revolusi. Pada saat pecah perang tahun 1792, ia menjadi kolonel dalam sebuah resimen kavaleri yang dikirim ke p...

Place in Styria, SloveniaČeče Sveta Katarina (until 1955)ČečeLocation in SloveniaCoordinates: 46°10′24.4″N 15°4′35.55″E / 46.173444°N 15.0765417°E / 46.173444; 15.0765417Country SloveniaTraditional regionStyriaStatistical regionCentral SavaMunicipalityTrbovlje, HrastnikArea • Total3.82 km2 (1.47 sq mi)Elevation561.6 m (1,842.5 ft)Population (2002) • Total303[1] Čeče (pronounced [ˈ...

Bulbophyllum beccarii Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Angiospermae (tanpa takson): Monocots Ordo: Asparagales Famili: Orchidaceae Genus: Bulbophyllum Spesies: Bulbophyllum beccarii Nama binomial Bulbophyllum beccariiRchb.f. 1879 Bulbophyllum beccarii adalah spesies tumbuhan yang tergolong ke dalam famili Orchidaceae. Spesies ini juga merupakan bagian dari ordo Asparagales. Spesies Bulbophyllum beccarii sendiri merupakan bagian dari genus Bulbophyllum.[1] Nama ilm...

Halaman ini memuat daftar paroki di Keuskupan Purwokerto. Daftar ini tidak dimaksudkan sebagai suatu daftar yang lengkap atau selalu terbarui. Jika Anda melihat artikel yang seharusnya tercantum di sini, silakan sunting halaman ini dan tambahkan pranala ke artikel tersebut. Gunakan perubahan terkait untuk melihat perubahan terbaru dari artikel-artikel yang tercantum pada halaman ini.[1][2][3] Daftar Dekanat Tengah Gambar Paroki Pelindung Lokasi Stasi/Kapel Paroki Kated...

Pour les personnes ayant le même patronyme, voir Tiberi. Jean Tiberi Jean Tiberi en 2007. Fonctions Maire du 5e arrondissement de Paris 2 avril 2001 – 13 avril 2014(13 ans et 11 jours) Prédécesseur Jean-Charles Bardon Successeur Florence Berthout 29 mars 1983 – 21 mai 1995(12 ans, 1 mois et 22 jours) Prédécesseur Fonction créée Successeur Jean-Charles Bardon Maire de Paris 16 mai 1995 – 25 mars 2001(5 ans, 10 mois et 9 jours) Électio...

For other people named Margaret of Bohemia, see Margaret of Bohemia (disambiguation). Queen consort of Denmark Dagmar of BohemiaQueen consort of DenmarkTenure1205–1212Bornc. 1186MeissenDied24 May 1212RibeBurialSt. Bendt's ChurchSpouseValdemar II of DenmarkIssueValdemar the YoungDynastyPřemyslidFatherOttokar I of BohemiaMotherAdelheid of Meissen Dagmar of Bohemia (also known as Margaret, Czech: Markéta; c. 1186 – 24 May 1212 in Ribe) was Queen of Denmark as the first spouse of King...

Artikel ini sebagian besar atau seluruhnya berasal dari satu sumber. Diskusi terkait dapat dibaca pada the halaman pembicaraan. Tolong bantu untuk memperbaiki artikel ini dengan menambahkan rujukan ke sumber lain yang tepercaya. Mengkudu Daun dan bunga dari Morinda citrifolia Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Angiospermae (tanpa takson): Eudikotil (tanpa takson): Asteridae Ordo: Gentianales Famili: Rubiaceae Genus: Morinda Spesies: M. citrifolia Nama binomial Morinda c...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne s'appuie pas, ou pas assez, sur des sources secondaires ou tertiaires (janvier 2024). Pour améliorer la vérifiabilité de l'article ainsi que son intérêt encyclopédique, il est nécessaire, quand des sources primaires sont citées, de les associer à des analyses faites par des sources secondaires. Scratch Interface de programmation de la version 3.0 Date de première version 2006 Paradigmes O...

Martin B-10Un Martin B-10 in voloDescrizioneTipobombardiere Equipaggio3 ProgettistaPeyton M. Magruder Costruttore Martin Co. Data primo volo16 febbraio 1932 Data entrata in serviziogiugno 1934 Utilizzatore principale USAAC Altri utilizzatori FAA Türk Hava Kuvvetleri Esemplari121 (B-10)32 (B-12)342 (tutte le varianti) Dimensioni e pesiTavole prospettiche Lunghezza13,6 m (44 ft 9 in) Apertura alare21,5 m (70 ft 6 in) Altezza4,7 m (15 ft 5 in) Superficie alare63 m² (678 ft²) Carico alare106 k...

1964 song by Nina Simone Don't Let Me Be MisunderstoodSingle by Nina Simonefrom the album Broadway-Blues-Ballads B-sideA MonsterReleased1964RecordedNew York CityGenre Blues jazz Length2:48LabelPhilipsSongwriter(s) Bennie Benjamin Horace Ott Sol Marcus Don't Let Me Be MisunderstoodSingle by the AnimalsB-sideClub a Go-GoReleased 29 January 1965 (U.K.) February 1965 (U.S.) Recorded16 November 1964[1]GenreBlues rockLength2:28Label Columbia Graphophone (UK) MGM (US) Songwriter(s) Bennie Be...
Implied covenant of honesty and fair dealing in contract law Contract law Formation Capacity Offer and acceptance Meeting of the minds2 Abstraction principle4,5 Posting rule1 Mirror image rule Invitation to treat Firm offer Consideration1,4 Implication-in-fact Collateral contract Defences Misrepresentation Mistake Threats and unequal bargaining power Illegality and public policy Unconscionability Culpa in contrahendo2 Force majeure Frustration of purpose Impossibility Impracticability Hardshi...

International AIDS activism, direct action and advocacy group For the City Girls song, see Act Up (song). AIDS Coalition to Unleash PowerAbbreviationACT UPFormationMarch 12, 1987PurposeHIV/AIDSKey peopleLarry KramerAffiliationsActUp/RIWebsiteactupny.comAIDS Coalition to Unleash Power (ACT UP) is an international, grassroots political group working to end the AIDS pandemic. The group works to improve the lives of people with AIDS through direct action, medical research, treatment and advocacy,...

2023 Louisiana elections ← 2022 October 14, 2023November 18, 2023 2024 → Elections in Louisiana Federal government Presidential elections 1812 1816 1820 1824 1828 1832 1836 1840 1844 1848 1852 1856 1860 1864 1868 1872 1876 1880 1884 1888 1892 1896 1900 1904 1908 1912 1916 1920 1924 1928 1932 1936 1940 1944 1948 1952 1956 1960 1964 1968 1972 1976 1980 1984 1988 1992 1996 2000 2004 2008 2012 2016 2020 2024 Presidential primaries Democratic 2000 2004 2008 2012 2016 2020 20...

Tiếng BasqueeuskaraSử dụng tạiTây Ban Nha, PhápKhu vựcXứ BasqueTổng số người nói750.000434,000 người hiểu nhưng không nói được[1]6,000 chỉ nói duy nhất tiếng Basque[2][3]Dân tộcBasquePhân loạiNgôn ngữ tách biệtNgôn ngữ tiền thânBasque nguyên thủy AquitaniTiếng Basque Phương ngữBiscay Gipuzkoa Thượng Navarre Hạ Navarre–Labourd Đông Navarre Soule (Zuberoa) Hệ chữ viếtLatinh (biến thể t...

Secondo avventofumetto Disegni di Adi Granov Titolo orig.Second Coming Lingua orig.inglese PaeseStati Uniti TestiMike Carey, Matt Fraction, Craig Kyle, Christopher Yost, Zeb Wells DisegniMike Choi, Terry Dodson, David Finch, Greg Land, Ibraim Roberson EditoreMarvel Comics Collana 1ª ed. X-Men: Second Coming New Mutants Uncanny X-Men X-Force X-Men: Legacy 1ª edizionemarzo – luglio 2010 Periodicitàmensile Albi14 (comp...

John HawkesHawkes tahun 2009LahirJohn Marvin Perkins11 September 1959 (umur 64)Alexandria, Minnesota, Amerika SerikatPekerjaanAktorTahun aktif1985–sekarang John Hawkes (lahir John Marvin Perkins tanggal 11 September 1959) merupakan seorang aktor Amerika Serikat. Ia dikenal dengan perannya sebagai pecandu methamphetamine Teardrop Dolly dalam film Winter's Bone, di mana ia mendapatkan nominasi Academy Award kategori aktor pendukung terbaik. Ia juga berperan sebagai Mark O'Brien dal...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: き゜ – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL (2019年12月) 本来の表記は「き゚」です。この記事に付けられ�...

Primera División(UNAFUT)2004-2005 Généralités Sport Football Édition 83e Date du 21 août 2004au 28 mai 2005 Palmarès Tenant du titre Deportivo Saprissa Promu(s) AD Belén Navigation Saison précédente Saison suivante modifier La Primera División 2004-2005 est la quatre-vingt-troisième édition de la première division costaricienne. Lors de ce tournoi, le Deportivo Saprissa a tenté de conserver son titre de champion du Costa Rica face aux onze meilleurs clubs costariciens. La sais...

Roman laws, 82–80 BCE Politics of ancient Rome Periods Roman Kingdom753–509 BC Roman Republic509–27 BC Roman Empire27 BC – AD 395 Principate27 BC – AD 284 DominateAD 284–641 WesternAD 395–476 EasternAD 395–1453 Timeline Constitution Kingdom Republic Sullan republic Empire Augustan reforms Late Empire Political institutions Imperium Collegiality Auctoritas Roman citizenship Cursus honorum Assemblies Centuriate Curiate Plebeian Tribal Ordinary magistrates Consul Praetor Quaestor...
この項目には、JIS X 0213:2004 で規定されている文字(ハートマーク)が含まれています(詳細)。 宮本 佳林 LIVE 2024春〜Hello! Brand new me〜RETURNS 2024年5月12日 広島公演基本情報出生名 宮本 佳林愛称 カリン[1][2]出生日 (1998-12-01) 1998年12月1日(25歳)[3]血液型 O型[3]出生・出身地 日本・千葉県[3]ジャンル J-POP職業 歌手活動期間 2008年[4] -レー...



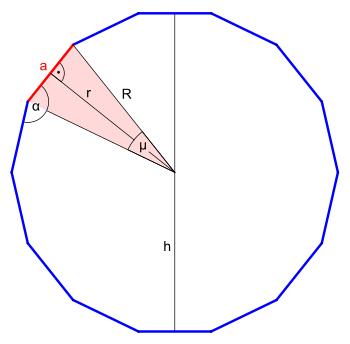

![{\displaystyle {\begin{aligned}a&=R\cdot 2\cdot \sin \left({\frac {180^{\circ }}{14}}\right)\\a&=R\cdot \left[{\frac {1}{2}}-{\frac {\sqrt {3}}{2}}\tan \left[{\frac {1}{3}}\arctan \left({\frac {\sqrt {3}}{9}}\right)\right]\right]\\a&\approx 0{,}4450418\cdot R\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/863319eda1f66c95402760a3b8adfefc98664bac)






































































































