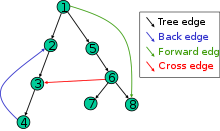
Tiefensuche
|
Read other articles:

American baseball player (1932–2019) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Tex Clevenger – news · newspapers · books · scholar · JSTOR (August 2019) (Learn how and when to remove this template message) Baseball player Tex ClevengerPitcherBorn: (1932-07-09)July 9, 1932Visalia, California, U.S.Died...

For Paramount+ original TV shows, see List of Paramount+ original programming. For films made available through the TVING content hub, see List of TVING original programming. This article lists all films, documentary films and specials produced for release on Paramount+, formerly known as CBS All Access, an American over-the-top subscription video on demand service owned and operated by Paramount Streaming, a division of Paramount Global. Original films Feature films Title Genre Release date...

Päijät-Häme Päijänne-TavastlandTavastia PäijänneRegionRegion Päijät-HämePäijät-Hämeen maakuntacode: fi is deprecated (Finlandia)Landskapet Päijänne-Tavastlandcode: sv is deprecated (Swedia) BenderaLambang kebesaranPäijät-Häme di peta FinlandiaNegaraFinlandiaProvinsi historisTavastiaIbukotaLahtiLuas • Total6.256,66 km2 (2,415,71 sq mi) • Luas daratan5.126,11 km2 (1,979,20 sq mi)Populasi (2019)&...

Listes de films américains ◄◄ 1935 1936 1937 1938 1939 1940 1941 1942 1943 ►► Liste (non exhaustive) de films américains sortis en 1939. Gone with the Wind remporte l'Oscar du meilleur film à la 12e cérémonie des Oscars organisée le 29 février 1940. (ordre alphabétique des titres en anglais) Titre comportant un nombre Titre Réalisateur Distribution Genre Notes $1000 a Touchdown James Patrick Hogan Joe E. Brown, Martha Raye, Eric Blore, Susan Hayward Comédie Paramount 2...

Sayaka SatoInformasi pribadiKebangsaanJepangLahir29 Maret 1991 (umur 33)Sendai, JepangTempat tinggalKanagawa, JepangTinggi171 m (561 ft 0 in)Berat70 kg (154 pon)PeganganKiriTunggal putriPeringkat tertinggi12 (10 November 2016)Peringkat saat ini416 (17 Maret 2020) Rekam medali Putri badminton Mewakili Jepang Piala Uber 2018 Bangkok Women's team 2010 Kuala Lumpur Women's team 2012 Wuhan Women's team 2016 Kunshan Women's team Asian Games 2018 Jakarta...

Disambiguazione – Se stai cercando altri significati, vedi Coppa Libertadores 2012 (disambigua). Coppa Libertadores 2012Copa Santander Libertadores de América 2012 Competizione Coppa Libertadores Sport Calcio Edizione 53ª Organizzatore CONMEBOL Date 24 gennaio 2012 - 4 luglio 2012 Partecipanti 38 Risultati Vincitore Corinthians(1º titolo) Secondo Boca Juniors Semi-finalisti Universidad de Chile Santos Statistiche Miglior marcatore Matías Alustiza Neymar (8 g...

1967 Italian comedy film ArabellaTheatrical release posterDirected byMauro BologniniWritten byGiorgio ArlorioAdriano BaraccoBrunello RondiProduced byMaleno MalenottiStarringVirna LisiJames FoxMargaret RutherfordTerry-ThomasCinematographyEnnio GuarnieriEdited byEraldo Da RomaMusic byEnnio MorriconeDistributed byUniversal PicturesRelease date 1967 (1967) Running time105 minutes (Italy)CountryItalyLanguageEnglish Arabella is an Italian comedy film in the English language, starring Virna Lis...

Sekretariat Komite Pusat Partai Komunis Uni Soviet Секретариат ЦК КПСС PimpinanStatusBadan pemerintahan pusat Partai Komunis Uni Soviet PemimpinSekretaris Umum Dipilih olehKomite Pusat Bertanggung jawab untukKomite Pusat AnggotaBeragamTempat bersidangLapangan Staraya, Moskwa, SFSR Rusia[1] L • BBantuan penggunaan templat ini Sekretariat Komite Pusat Partai Komunis Uni Soviet adalah sebuah badan yang bertanggung jawab untuk pemerintahan pusat dari partai tersebu...

MuşMunisipalitasMuşKoordinat: 38°44′00″N 41°29′28″E / 38.73333°N 41.49111°E / 38.73333; 41.49111Koordinat: 38°44′00″N 41°29′28″E / 38.73333°N 41.49111°E / 38.73333; 41.49111NegaraTurkiProvinsiMuşPemerintahan • WalikotaFeyat Asya (AKP)Luas[1] • Distrik2.604,14 km2 (100,546 sq mi)Ketinggian1.350 m (4,430 ft)Populasi (2012)[2] • Perkotaan81....

Почесні звання України Почесне звання України — державна нагорода України. Почесні звання України присвоюються особам, які працюють у відповідній галузі економічної та соціально-культурної сфери, як правило, не менше десяти років, мають високі трудові досягнення і п...

Election in Hawaii Main article: 1984 United States presidential election 1984 United States presidential election in Hawaii ← 1980 November 6, 1984 1988 → Nominee Ronald Reagan Walter Mondale Party Republican Democratic Home state California Minnesota Running mate George H. W. Bush Geraldine Ferraro Electoral vote 4 0 Popular vote 185,050 147,154 Percentage 55.10% 43.82% County Results Reagan 50–60% President before election ...
فلوموكسيف الاسم النظامي (6R,7R)-7-[[2-(Difluoromethylsulfanyl)acetyl]amino]-3- [[1-(2-hydroxyethyl)tetrazol-5-yl]sulfanylmethyl]-7-methoxy-8-oxo-5-oxa-1-azabicyclo[4.2.0]oct-2-ene-2-carboxylic acid اعتبارات علاجية ASHPDrugs.com أسماء الدواء الدولية معرّفات CAS 99665-00-6 Y ك ع ت J01J01DC14 DC14 تصنيف منظمة الصحة العالمية المراقبة [لغات أخرى][1] بوب ك�...

Software developer Wrightsoft Corp.Company typePrivateFounded1985HeadquartersLexington, Massachusetts, USAKey peopleBill Wright:President & CEOChris Edgren:Vice President Sales & MarketingMichael Shnitman:Vice President Software DevelopmentCharles S. Chip BarnabyVice President ResearchWebsitewww.wrightsoft.com Wrightsoft is a software development firm for heating, ventilation, and air conditioning (HVAC). Established in 1985,[1] Wrightsoft has served residential, commercial, a...

American Association of Colleges of NursingLogo of AACNAbbreviationAACNFormation1969Headquarters655 K Street, NW Suite 750 Washington, D.C., United StatesMembership 876 membersBoard ChairJean Giddens, PhD, RNPresident/CEODeborah E. Trautman, PhD, RNWebsitewww.aacnnursing.org The American Association of Colleges of Nursing (AACN) is a national organization of nurses in the United States that is dedicated to advancing nursing education. It was established in 1969, and represents more than 875 m...

第三十二届夏季奥林匹克运动会男子400米比賽比賽場館新国立竞技场日期2021年8月1日(预赛)2021年8月2日(半决赛)2021年8月5日(决赛)参赛选手48位選手,來自33個國家和地區冠军成绩43.85奖牌获得者01 ! 史蒂文·加德纳 巴哈马02 ! 安东尼·桑布拉诺 哥伦比亚03 ! 基拉尼·詹姆斯 格林纳达← 20162024 → 2020年夏季奥林匹克运动会田径比赛径赛1...

Questa voce sull'argomento dipinti è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Hélène Fourment con due dei suoi figliAutorePeter Paul Rubens Data1636 Tecnicaolio su tela Dimensioni115×85 cm UbicazioneMusée du Louvre, Parigi Hélène Fourment con due dei suoi figli è un dipinto (115x85 cm) realizzato nel 1636 circa dal pittore Peter Paul Rubens. È conservato nel Musée du Louvre di Parigi...

عرق بارز من الكوارتز بين صخور خاضعة لعوامل الحت والتعرية العرق في الجيولوجيا عبارة عن تجمع متمايز لكتل من معدن متبلور داخل الصخور. تتشكل العروق عندما تُحمَل المكونات المعدنية من قبل المحاليل المائية داخل كتلة الصخرة ثم تحدث عليها عملية ترسيب؛ ويكون جريان الموائع الواقع و�...

Aeropuerto de Aarhus Aarhus Lufthavn IATA: AAR OACI: EKAH FAA: LocalizaciónUbicación Kolind, DinamarcaElevación 25Sirve a AarhusDetalles del aeropuertoTipo CivilPropietario Aarhus (municipio)Operador Aarhus Lufthavn A/SPistas DirecciónLargoSuperficie10L/28R2.777Asfalto10R/28L2.702AsfaltoMapa AAR / EKAH Ubicación en DinamarcaSitio web https://www.aar.dk/[editar datos en Wikidata] El Aeropuerto de Aarhus (IATA: AAR, OACI: EKAH) es un aeropuerto civil ubicado en Tirstrup, Din...

Lingua franca har två betydelser. I nutida språkvetenskapliga sammanhang betecknar det generellt ett språk som används vid kommunikation mellan människor som inte förstår varandras modersmål. Historiskt betecknar det också ett specifikt pidginspråk med samma funktion. Detta utvecklades i Medelhavsområdet under korstågstiden men är idag utdött.[1] Historia Termen lingua franca användes för första gången av franska och italienska korsfarare i medelhavsområdet för att kommuni...

American radio network This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Salem Radio Network – news · newspapers · books · scholar · JSTOR (November 2022) (Learn how and when to remove this message) Salem Radio NetworkTypeRadio networkCountryUnited StatesOwnershipOwnerSalem Media GroupHistoryLaunch date2009Cov...