Sprungprozess
|
Read other articles:

Halaman ini berisi artikel tentang raja Kediri yang terkenal. Untuk Kertajaya (disambiguasi), lihat Kertajaya (disambiguasi). KertajayaPaduka Sri Maharaja Sri Sarweswara Triwikramawatara Anindita Srengga Lancana Digjaya UttunggadewaRaja Panjalu terakhirBerkuasa1194 - 1222PendahuluKameswaraInformasi pribadiKelahiranDahaJawa TimurKematian1222Pertempuran Ganter, Ngantang, Kabupaten Malang, Jawa TimurWangsaIsyanaAnakJayasabhaAgamaHindu Sri Maharaja Srengga atau Kertajaya, di dalam Pararaton diseb...

العلاقات السويسرية الفيجية سويسرا فيجي سويسرا فيجي تعديل مصدري - تعديل العلاقات السويسرية الفيجية هي العلاقات الثنائية التي تجمع بين سويسرا وفيجي.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة سويسرا فيج...

1937 American filmPopeye the Sailor Meets Ali Baba's Forty ThievesDirected byDave Fleischer[1]Willard Bowsky(animation - uncredited)Story byDan Gordon (story)Bill Turner (uncredited)Jack Ward (story) (uncredited)Izzy Sparber (uncredited)Seymour Kneitel (uncredited)Based onAli Baba and the Forty ThievesProduced byMax Fleischer[1]Adolph ZukorStarringJack MercerMae QuestelGus WickieLou Fleischer[1]Music bySammy TimbergSammy LernerTot Seymour (Abu Hassan lyricist)Vee Lawn...

1967 novel by Samuel Delany The Einstein Intersection First edition (paperback)AuthorSamuel R. DelanyCover artistJack GaughanCountryUnited StatesLanguageEnglishGenreScience fiction novelPublisherAce BooksPublication date1967Media typePrint (hardback & paperback)Pages142 pp The Einstein Intersection is a 1967 science fiction novel by Samuel R. Delany. The title is a reference to Einstein's Theory of Relativity connecting to Kurt Gödel's Constructible universe, which is an analog...

يوم الهانغل (هانغل: 조선글날) صفحة من هنمنجونغوم يحتفل به كوريا الجنوبية، كوريا الشمالية نوعه قومي، ثقافي اليوم السنوي 9 أكتوبر (كوريا الجنوبية)15 يناير (كوريا الشمالية) تعديل مصدري - تعديل يوم الأبجدية الكورية أو يوم الهانغول هو عيد وطني في كوريا في ذكرى اختراع الهان�...

1953 Dutch Grand Prix ← Previous raceNext race → Zandvoort original layoutRace detailsDate 7 June 1953Official name IV Grote Prijs van NederlandLocation Circuit Park Zandvoort, Zandvoort, NetherlandsCourse Permanent racing facilityCourse length 4.193 km (2.605 miles)Distance 90 laps, 377.370 km (234.488 miles)Weather Sunny, mild, dryPole positionDriver Alberto Ascari FerrariTime 1:51.1Fastest lapDriver Luigi Villoresi FerrariTime 1:52.8 on lap 59PodiumFirst Alberto Asc...

Coppa di Svezia 2012-2013Svenska Cupen 2012-2013 Competizione Svenska Cupen Sport Calcio Edizione 57ª Organizzatore SvFF Date dal 5 agosto 2012al 26 maggio 2013 Luogo Svezia Partecipanti 96 (103 alle qualificazioni) Risultati Vincitore IFK Göteborg(6º titolo) Secondo Djurgården Statistiche Incontri disputati 119 Gol segnati 407 (3,42 per incontro) Cronologia della competizione 2011 2013-2014 Manuale La Coppa di Svezia 2012-2013 (in svedese Svenska Cupen) è...

Права Права людини громадянські та політичні економічні, соціальні та культурні три покоління Права бенефіціарів ЛГБТ (трансгендери)глухігромадянидітижінкикоролікорінні народикредиторилюдименшиниобвинуваченіроботирослиниселяниспоживачітвариничоловікиінваліди...

English Conservative politician The Right HonourableThe Baroness Scott of BybrookOBEOfficial portrait, 2018 Parliamentary Under-Secretary of State for Social Housing and Faith[1]IncumbentAssumed office 20 September 2022Prime MinisterLiz TrussRishi Sunak[2]Baroness-in-WaitingGovernment WhipIn office14 February 2020 – 20 September 2022Prime MinisterBoris JohnsonPreceded byThe Baroness SaterLeader of the Wiltshire CouncilIn office1 April 2009 – 10 July 2...

У этого термина существуют и другие значения, см. Чайки (значения). Чайки Доминиканская чайкаЗападная чайкаКалифорнийская чайкаМорская чайка Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:Вторич...

National personification of Germany For other uses, see Germania (disambiguation). Germania painting from 1848, by Philipp Veit. This image once covered the old organ inside the Paulskirche, above where the Frankfurt Parliament assembled from 1848 to 1849. Figure of Germania atop the Niederwalddenkmal in the Rhine valley, dedicated 1883 Germania (/dʒərˈmeɪniə/; Latin: [ɡɛrˈmaːnia]) is the personification of the German nation or the Germans as a whole. Like many other national...

1980 film by François Truffaut For the earlier film, see The Last Metro (1945 film). The Last MetroFilm posterDirected byFrançois TruffautWritten byFrançois TruffautSuzanne SchiffmanJean-Claude GrumbergProduced byFrançois TruffautJean-José RicherStarringCatherine DeneuveGérard DepardieuJean PoiretCinematographyNéstor AlmendrosEdited byMartine BarraquéMusic byGeorges DelerueProductioncompaniesLes Films du CarrosseAndrea FilmsSEDIFSFPTF1 Films ProductionDistributed byGaumontRelease date...

American baseball pitcher (born 1987) Baseball player Blaine HardyHardy with the Detroit TigersPitcherBorn: (1987-03-14) March 14, 1987 (age 37)Seattle, Washington, U.S.Batted: LeftThrew: LeftMLB debutJune 16, 2014, for the Detroit TigersLast MLB appearanceAugust 3, 2021, for the Milwaukee BrewersMLB statisticsWin–loss record14–11Earned run average3.78Strikeouts230 Teams Detroit Tigers (2014–2019) Milwaukee Brewers (2021) Blaine Patrick Hardy (born Mar...

1987 studio album by Chick Corea Elektric BandLight YearsStudio album by Chick Corea Elektric BandReleased1987StudioMad Hatter Recording Studios (Los Angeles, CA)GenreJazz fusionLength60:25 (CD) 41:06 (vinyl)LabelGRPProducerChick CoreaChick Corea chronology The Chick Corea Elektric Band(1986) Light Years(1987) Eye of the Beholder(1988) Light Years is an album by the Chick Corea Elektric Band. It features Chick Corea with guitarist Frank Gambale, saxophonist Eric Marienthal, bassist Jo...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Amartha Hangtuah – berita · surat kabar · buku · cendekiawan · JSTOR Hangtuah Jakarta[[IBL Indonesia 2023]]DivisiPutihLigaIBL IndonesiaDibentuk1995; 29 tahun lalu (1995)SejarahHangtuah (2003-2008) H...

UFC mixed martial arts event in 2008 UFC Fight Night: Florian vs. LauzonThe poster for UFC Fight Night: Florian vs. LauzonInformationPromotionUltimate Fighting ChampionshipDateApril 2, 2008VenueBroomfield Event CenterCityBroomfield, ColoradoAttendance6,742[1]Total gate$753,429[1]Event chronology UFC 82: Pride of a Champion UFC Fight Night: Florian vs. Lauzon UFC 83: Serra vs. St-Pierre 2 UFC Fight Night: Florian vs. Lauzon[2] (also known as UFC Fight Night 13) was a mi...

Taiwanese–Hong Kong actress and model (born 1974) This article is about the actress. For the filmmaker, see Shu Kei. For the Guzhu royal prince during the Shang and Zhou dynasties, see Boyi and Shuqi. For the Malaysian politician, see Wong Shu Qi. In this Chinese name, the family name is Lin. Shu Qi舒淇Shu Qi in 2023BornLin Li-hui (1974-04-16) 16 April 1974 (age 50)Xindian, Taipei County, TaiwanNationalityHong Kong–TaiwaneseCitizenship Hong Kong Taiwan EducationNew Taipei Municipal...

CNN International Asia PacificDiluncurkan1 September 1985 (CNN International)1 Agustus 1989 (CNN International Asia Pacific)JaringanCNN InternationalPemilikCNN Global(Warner Bros. Discovery)SloganGo ThereNegara Hong Kong TaiwanWilayah siarAsia Tenggara, Oseania, Jepang, Korea Selatan, Hong Kong, Makau dan Taiwan (kecuali Tiongkok Daratan dan Korea Utara)Kantor pusatHong KongTaipei, TaiwanSitus webCNN.comCNN Asia CNN International Asia Pacific adalah edisi Asia-Pasifik dari jaringan ...

Gröben Huy hiệuVị trí của Gröben GröbenQuốc giaĐứcBangSachsen-AnhaltHuyệnBurgenlandkreisLiên xãVier Berge-Teucherner LandChính quyền • Thị trưởngIsolde FelschDiện tích • Tổng cộng3,94 km2 (152 mi2)Độ cao193 m (633 ft)Dân số (2006-12-31) • Tổng cộng715 • Mật độ1,8/km2 (4,7/mi2)Múi giờCET (UTC+01:00) • Mùa hè (DST)CEST (UTC+02:0...
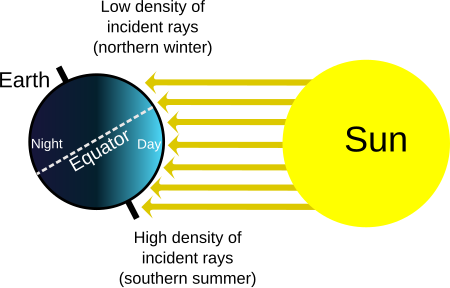
Subdivision of the year based on orbit and axial tilt For other uses, see Season (disambiguation). Part of a series onWeather Temperate and polar seasons Winter Spring Summer Autumn Tropical seasons Dry season Harmattan Wet season Storms Cloud Cumulonimbus cloud Arcus cloud Downburst Microburst Heat burst Derecho Lightning Volcanic lightning Thunderstorm Air-mass thunderstorm Thundersnow Dry thunderstorm Mesocyclone Supercell Tornado Anticyclonic tornado Landspout Waterspout Dust devil Fire w...















