Nilpotente Gruppe
|
Read other articles:

2002 2012 Élections législatives de 2007 dans le Gers 2 sièges de députés à l'Assemblée nationale 10 et 17 juin 2007 Corps électoral et résultats Inscrits 140 775 Votants au 1er tour 95 021 67,5 % 3,7 Votes exprimés au 1er tour 92 676 Votants au 2d tour 97 387 69,19 % Votes exprimés au 2d tour 93 947 Gauche parlementaire Liste Parti socialisteParti radical de gaucheLes VertsParti communiste françaisDivers gauche Voix au 1...

Ridge on the cerebral cortex of the brain For the video game, see Gyruss. Gyral redirects here. For the album, see Gyral (album). Not to be confused with Girus. GyrusGyrus and sulcusIdentifiersTA98A14.1.09.004TA25432FMA83874Anatomical terminology[edit on Wikidata] Gray's FIG. 726 – Lateral surface of left cerebral hemisphere, viewed from the side Gray's Fig. 727 – Medial surface of left cerebral hemisphere In neuroanatomy, a gyrus (pl.: gyri) is a ridge on the cerebral cortex. It is g...

Ethnic group in Asia Cocos MalaysMelayu KokosA Malay bride and bridegroom as seen in a wedding event in the Cocos (Keeling) Islands, 1912.Total population4,000–5,000[1]Regions with significant populations Malaysia ( Sabah): ~5,000[1] Australia ( Cocos (Keeling) Islands): 400LanguagesCocos Malay, English and MalaysianReligionMajority: Sunni Islam[2]Related ethnic groupsBantenese, Betawi people, Javanese people, Malays Cocos Malays are a community t...

Untuk ahli zoologi Hungaria, lihat Lajos Bíró (zoologist). Bentuk asli dari nama pribadi ini adalah Bíró Lajos. Artikel ini menggunakan rangkaian nama Barat. Lajos BíróLahirLajos Blau(1880-08-22)22 Agustus 1880Nagyvárad, Austria-Hungaria (sekarang Oradea, Bihor, Rumania)Meninggal9 September 1948(1948-09-09) (umur 68)London, Inggris, Britania RayaPekerjaanpenulisTahun aktif1917–1948 Makam Lajos Biro, Pemakaman Hampstead, London Lajos Bíró (lahir dengan nama Lajos Blau) (22...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

ヨハネス12世 第130代 ローマ教皇 教皇就任 955年12月16日教皇離任 964年5月14日先代 アガペトゥス2世次代 レオ8世個人情報出生 937年スポレート公国(中部イタリア)スポレート死去 964年5月14日 教皇領、ローマ原国籍 スポレート公国親 父アルベリーコ2世(スポレート公)、母アルダその他のヨハネステンプレートを表示 ヨハネス12世(Ioannes XII、937年 - 964年5月14日)は、ロ...

Військово-музичне управління Збройних сил України Тип військове формуванняЗасновано 1992Країна Україна Емблема управління Військово-музичне управління Збройних сил України — структурний підрозділ Генерального штабу Збройних сил України призначений для планува...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Bethesda Hospital Ambur – news · newspapers · books · scholar · JSTOR (October 2011) This ar...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Sudanese society – news · newspapers · books · scholar · JSTOR (October 2020) Sudanese society was very much in flux in the 2000s.[1] Various factors included: rural to urban migration; the large numbers of displaced persons—foreign and nati...
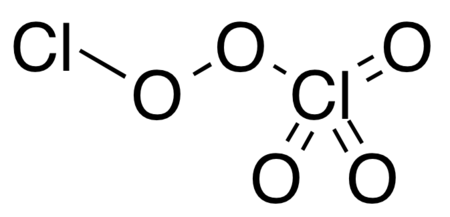
Dichlorine pentoxide Names IUPAC name Dichlorine pentoxide Identifiers CAS Number 264271-80-9 (trioxo[μ-(peroxy-κO:κO')]dichlorine) Y224299-16-5 (perchloryl chloride peroxide) Y 3D model (JSmol) Interactive image PubChem CID 153991604 (perchloryl chloride peroxide)154081050 (chloryl chlorate) SMILES ClOOCl(=O)(=O)=O Properties Chemical formula Cl2O5 Molar mass 150.90 g·mol−1 Related compounds Related compounds Dichlorine heptoxide Except where ...

Cet article est une ébauche concernant une localité argentine. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Quitilipi Héraldique Administration Pays Argentine Province Chaco Département Quitilipi Maire Alfredo Osvaldo Zamora Code postal H3530 Démographie Population 20 737 hab. (2001) Géographie Coordonnées 26° 52′ 13″ sud, 60° 12′ 54″ ouest Altitu...

2007 single by Jonas BrothersHold OnSingle by Jonas Brothersfrom the album Jonas Brothers B-sideTake a BreathReleasedMay 22, 2007 (2007-05-22)RecordedFebruary 2007GenreArena rock[1]pop punkpower popLength2:45LabelHollywoodSongwriter(s) Nicholas Jonas Joseph Jonas Kevin Jonas II Producer(s)John FieldsJonas Brothers singles chronology Year 3000 (2006) Hold On (2007) S.O.S (2007) Music videoHold On on YouTube Hold On is a song by American pop rock band Jonas Brothers. The ...

Biblical figure and monarch For other uses, see Jeroboam (disambiguation). JeroboamירבעםDetail of Jeroboam Sacrificing to Idols by Fragonard, 1752King of Northern IsraelReign931/22 – 910/901 BC (tentative)PredecessorPosition establishedSuccessorNadabBornunknownUnited Kingdom of IsraelDied910/901 BC (tentative)Tirzah, Northern Kingdom of IsraelSpouseAno (named only in the Septuagint)IssueAbijah NadabHouseNew House, Tribe of EphraimFatherNebatMotherZeruah Jeroboam I (/ˌdʒɛrəˈ...

В Википедии есть статьи о других людях с фамилией Леблан. Морис Лебланфр. Marie Émile Maurice Leblanc Имя при рождении фр. Marie Émile Maurice Leblanc Дата рождения 11 декабря 1864(1864-12-11)[1] или 11 ноября 1864(1864-11-11)[2] Место рождения Руан Дата смерти 6 ноября 1941(1941-11-06)[1][3][…] (76 ле�...

Le terme de « social-impérialisme » est une expression utilisée par les mouvements politiques d'inspiration marxiste pour dénoncer, de manière péjorative, les organisations ou les États qui sont « socialistes dans les mots, impérialistes dans les actions » [1]. La phrase a été utilisée pour la première fois dans les cercles marxistes au cours des discussions du début du XXe siècle sur la position de l’Internationale ouvrière concernant l’imminenc...

The Mind & Brain Prize was established in 2003 and aims at honouring the most relevant researchers in the field of cognitive science, as well as to recognize outstanding achievement in advancing knowledge about mind and brain by persons whose work contributed to the growth and development of the discipline.[1][2] It is awarded by the University and Polytechnic of Turin.[citation needed] Laureates Giacomo Rizzolatti, first Mind & Brain Prize laureate [3]...

Questa voce o sezione sull'argomento nobili è priva o carente di note e riferimenti bibliografici puntuali. Sebbene vi siano una bibliografia e/o dei collegamenti esterni, manca la contestualizzazione delle fonti con note a piè di pagina o altri riferimenti precisi che indichino puntualmente la provenienza delle informazioni. Puoi migliorare questa voce citando le fonti più precisamente. Giacomo Durazzo Il conte Giacomo Durazzo (Genova, 27 aprile 1717 – Venezia, 15 ottobre 1794) è...

Presidents of the United States redirects here. For other uses, see President of the United States (disambiguation). The White House, official residence of the president of the United States, in July 2008 The president of the United States is the head of state and head of government of the United States,[1] indirectly elected to a four-year term via the Electoral College.[2] The officeholder leads the executive branch of the federal government and is the commander-in-chief of...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أبريل 2019) كريستينا بيرغر معلومات شخصية الميلاد 20 يونيو 1988 (36 سنة) ألمانيا مواطنة ألمانيا الحياة العملية المهنة نبَّالة اللغات الألمانية الرياضة القوس...
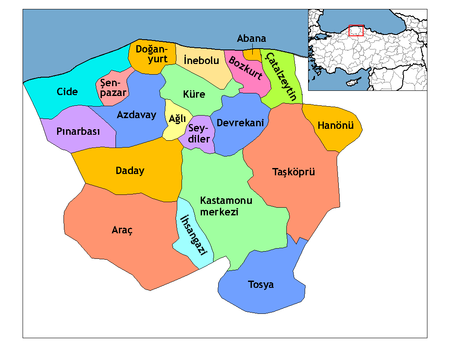
Cet article est une ébauche concernant la Turquie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Kastamonu (province) Monument de la République de Kastamonu Administration Pays Turquie Région Région de la mer Noire Capitale Kastamonu Indicatif téléphonique international +(90) Plaque minéralogique 37 Démographie Population 388 990 hab. (2023[1],[2]) Densité 29 hab./km2 Géographie Superf...

![{\displaystyle L_{n}(G):=[L_{n-1}(G),G]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/998d22c011032b8eed4ff63af104f2a458331627)





























