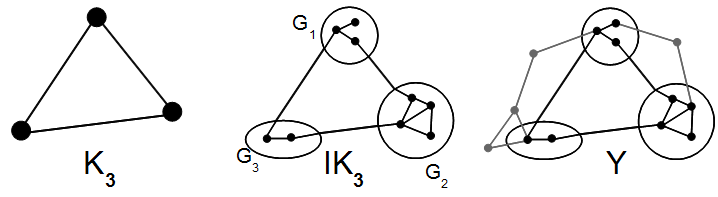
Minor (Graphentheorie)
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Lemon TreeSingel oleh Fool's Gardendari album Dish of the DaySisi-BFinallyDirilisApril 1995 (1995-04) (AS)April 1995 (1995-04) (CD single)FormatCD singleDirekam1994GenrePopDurasi03.11LabelIntercordPencipta Peter Freudenthaler Volker Hinkel Pr...

Yang MuliaFuat OktayOktay in 2019 Wakil Presiden Turki ke-1Masa jabatan10 Juli 2018 – 4 Juni 2023PresidenRecep Tayyip Erdoğan PendahuluDidirikanPenggantiCevdet YılmazAnggota Majelis Agung Nasional TurkiPetahanaMulai menjabat 2 Juni 2023Daerah pemilihanAnkara (III) (2023)Wakil Perdana Menteri TurkiMasa jabatan18 Juni 2016 – 9 Juli 2018Perdana MenteriBinali Yıldırım PendahuluKemal MadenoğluPenggantiDibubarkanDirektur Kepresidenan Penanggulangan Bencana dan Darur...

كرة القدم في دورة الألعاب العربية 1997معلومات عامةالرياضة كرة القدم جزء من دورة الألعاب العربية 1997 الفترة 1997 عدد الجولات 16 المواسمكأس العرب 1992 كرة القدم في دورة الألعاب العربية 1999 تعديل - تعديل مصدري - تعديل ويكي بيانات كرة القدم في دورة الألعاب العربية 1997 البلد لبنان الت�...

Astronaut employed by a company instead of a government This article is about commercial spacefarers. For paying space travellers, see Space tourism. Commercial astronautPatti Grace Smith presents SpaceShipOne pilot Mike Melvill the department's first commercial astronaut wings.OccupationOccupation typeProfessionDescriptionCompetenciesSee astronaut trainingFields ofemploymentSpace explorationRelated jobsAstronaut A commercial astronaut is a person who has commanded, piloted, or served as an a...

History of law enforcement for Queensland, Australia Governor of Queensland inspecting the mounted police, Brisbane, circa 1940 The history of the Queensland Police Service in Queensland, Australia, commenced in 1864, five years after the Separation of Queensland from New South Wales in 1859. This timeline highlights significant developments in Queensland policing. 1860s The uniform worn by Queensland police officers after separation in 1859 was a dark blue jacket and top with a forage cap, s...

Metabolic reaction This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Substrate-level phosphorylation – news · newspapers · books · scholar · JSTOR (November ...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Condet – berita · surat kabar · buku · cendekiawan · JSTOR Gardu Kayu Manis Salak condet RPTRA Muara Condet, Jakarta Timur. Grup latihan Pencak silat di RPTRA Muara Condet, Kramat Jati Jakarta Timur. Con...

Emmy SaelanLahir(1924-10-15)15 Oktober 1924Malangke, Hindia BelandaMeninggal24 Januari 1947(1947-01-24) (umur 22)Makassar, Sulawesi, IndonesiaDikenal atasPahlawan Nasional Indonesia, Pejuang perempuan yang gagah berani Emmy Saelan (15 Oktober 1924 – 24 Januari 1947) adalah salah seorang pejuang wanita dan Pahlawan Nasional Indonesia.[1] Ayahnya bernama Amin Saelan, adalah tokoh pergerakan taman siswa di Kota Makassar dan sekaligus penasehat organisasi pemuda. Sal...

UAV squadron of the US Navy Unmanned Patrol Squadron 19VUP-19 InsigniaActive4 July 1946 – 31 August 1991; 1 October 2013 (2013-10-01)- ()CountryUnited States of AmericaBranchUnited States NavyTypesquadronRoleMaritime patrolPart ofPatrol and Reconnaissance Wing 11Garrison/HQNaval Air Station Jacksonville, FloridaNickname(s)Big RedEngagementsKorean WarVietnam WarAircraft flownPatrolPV-2 HarpoonPBY-5A/6A CatalinaP-2 NeptuneP4Y-2/2S PrivateerP-3 OrionNorthrop Grumman MQ...

У этого термина существуют и другие значения, см. Чайки (значения). Чайки Доминиканская чайкаЗападная чайкаКалифорнийская чайкаМорская чайка Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:Вторич...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The topic of this article may not meet Wikipedia's notability guideline for biographies. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is likely to b...

Men's 10 metre platformat the Games of the XX OlympiadMedalists Klaus Dibiasi Italy Richard Rydze United States Giorgio Cagnotto Italy← 19681976 → Diving at the1972 Summer Olympics3 m springboardmenwomen10 m platformmenwomenvte The men's 10 metre platform, also reported as platform diving, was one of four diving events on the Diving at the 1972 Summer Olympics programme.[1] The competition was split into two phases: Preliminary round (3 Septemb...

Військово-музичне управління Збройних сил України Тип військове формуванняЗасновано 1992Країна Україна Емблема управління Військово-музичне управління Збройних сил України — структурний підрозділ Генерального штабу Збройних сил України призначений для планува...
عنتمدن فلسطين التاريخيةالعاصمة القدسمدن فلسطينية في الضفة الغربية جنين ( جنين، قباطية) طوباس (طوباس) طولكرم (طولكرم) نابلس ( نابلس) سلفيت ( سلفيت) قلقيلية (قلقيلية) رام الله والبيرة ( رام الله، البيرة، بيتونيا) أريحا ( أريحا) القدس (أبو ديس، العيزرية) بيت لحم ( ...

County in Washington, United States This article is about Pacific County, Washington. For the city in King and Pierce counties, see Pacific, Washington. County in WashingtonPacific CountyCountyPacific County Courthouse, South BendLocation within the U.S. state of WashingtonWashington's location within the U.S.Coordinates: 46°34′N 123°47′W / 46.56°N 123.78°W / 46.56; -123.78Country United StatesState WashingtonFoundedFebruary 4, 1851Named forPacific Oc...

PichanaquidistrettoMunicipalidad distrital de Pichanaqui LocalizzazioneStato Perù Regione Junín ProvinciaChanchamayo AmministrazioneCapoluogoBajo Pichanaqui Data di istituzione24 settembre 1977 TerritorioCoordinatedel capoluogo10°55′28.83″S 74°52′36.49″W10°55′28.83″S, 74°52′36.49″W (Pichanaqui) Altitudine525 m s.l.m. Superficie1 496,59 km² Abitanti40 625 (2005) Densità27,15 ab./km² Altre informazioniLinguespagnolo Fuso orarioUTC-5 C...

Elder sister of Theodore Roosevelt (1855–1931) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Bamie Roosevelt – news · newspapers · books · scholar · JSTOR (May 2022) (Learn how and when to remove this message) Anna Roosevelt CowlesBornAnna Roosevelt(1855-01-18)January 18, 1855New York City, U.S.DiedAugus...

Irfing Jaya Waketbidakademik STIK Lemdiklat Polri Informasi pribadiLahir19 Juni 1968 (umur 56)Pangkal Pinang, Kepulauan Bangka BelitungAlma materAkademi Kepolisian (1992)Karier militerPihak IndonesiaDinas/cabang Kepolisian Negara Republik IndonesiaMasa dinas1992—sekarangPangkat Brigadir Jenderal PolisiNRP66090438SatuanPendidikan PolriSunting kotak info • L • B Brigjen. Pol. Irfing Jaya, S.I.K., M.H. (lahir 19 Juni 1968) adalah seorang perwira tinggi Polri yang s...

United States historic placeEllen M. Smith Three-DeckerU.S. National Register of Historic Places c. 1981 photoShow map of MassachusettsShow map of the United StatesLocation22 Kilby St.,Worcester, MassachusettsCoordinates42°15′2″N 71°48′58″W / 42.25056°N 71.81611°W / 42.25056; -71.81611Built1908 (1908)Architectural styleQueen AnneMPSWorcester Three-Deckers TRNRHP reference No.89002409[1]Added to NRHPFebruary 9, 1990 The Ellen M. S...

Auburncity(EN) City of Auburn, New York Auburn – Veduta LocalizzazioneStato Stati Uniti Stato federato New York ConteaCayuga AmministrazioneSindacoMichael Quill (D) TerritorioCoordinate42°56′N 76°34′W42°56′N, 76°34′W (Auburn) Altitudine209 m s.l.m. Superficie21,8 km² Abitanti27 317 (01-07-2007) Densità1 253,07 ab./km² Altre informazioniCod. postale13021, 13022, 13024 Prefisso315 Fuso orarioUTC-5 CartografiaAuburn Sito istituzionaleModifica ...