Leon Bankoff (* 13. Dezember 1908 in New York City; † 16. Februar 1997 in Los Angeles) war ein amerikanischer Zahnarzt und Mathematiker.
Leben
Nach dem Besuch des City College of New York studierte Bankoff Zahnmedizin an der New York University; später wechselte er nach Los Angeles, Kalifornien, wo er an der University of Southern California sein Studium vollendete. Er praktizierte über 60 Jahre lang als Zahnarzt in Beverly Hills (Los Angeles); zahlreiche Hollywood-Prominente zählten zu seinen Patienten.
Sein Interesse galt aber keineswegs nur der Zahnheilkunde: Er sprach fließend Esperanto, spielte Klavier und Gitarre, schuf künstlerische Skulpturen und interessierte sich für die fortschreitende Entwicklung der Computertechnik – vor allem aber war er ein in der mathematischen Fachwelt hochangesehener Experte auf dem Gebiet der ebenen Geometrie und zählte die bedeutendsten Mathematiker seiner Zeit zu seinen Freunden. Er hielt Vorträge und veröffentlichte ab den 1940er Jahren zahlreiche Fachartikel, als Koautor von Paul Erdős hatte Bankoff die Erdős-Zahl 1[1] (s. hierzu auch die Liste der Fachartikel).
Von 1968 bis 1981 war Bankoff Editor des Problem Department des Pi Mu Epsilon Journals, wo er für die Publikation von rund 300 hochkarätigen Problemen aus dem Bereich der ebenen Geometrie verantwortlich war.
|
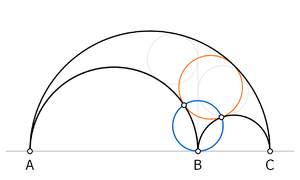
Der Arbelos (schwarz) mit den Zwillingskreisen des Archimedes (hellgrau) und Bankoffs drittem Kreis (blau).
Orange: der Inkreis des Arbelos
|
Seine besondere Leidenschaft galt dem Arbelos, einer geometrischen Figur mit verblüffenden Eigenschaften, die vermutlich erstmals von Archimedes untersucht wurde. Über 2000 Jahre, nachdem Archimedes im Arbelos die Zwillingskreise entdeckt hatte, konnte Bankoff im Jahre 1954 einen dritten zu den Zwillingskreisen kongruenten Kreis und 1974 einen vierten nachweisen − die später nach ihm benannten Bankoff-Kreise. Er publizierte seine Entdeckungen 1974 in einem viel beachteten Artikel[2] und inspirierte damit andere Mathematiker und mathematisch Interessierte, die im Laufe der folgenden 30 Jahre Dutzende weitere archimedische Kreise entdeckten.[3]
Nach der Aufgabe seiner Zahnarztpraxis begann Bankoff mit der Arbeit an einem umfassenden Buch über den Arbelos, basierend u. a. auf Material von Victor Thébault (1882–1960), einem französischen Mathematiker. Er konnte sein Manuskript nicht vollenden – 1997 starb er an einem Krebsleiden.
Siehe auch
Bankoff befasste sich u. a. mit den folgenden geometrischen Figuren, zu deren Erforschung er wesentlich beitrug (s. Liste der Fachartikel):
Quellen
- ↑ Liste der Personen mit Erdős-Zahl 1 auf der Seite des Erdős Number Project.
- ↑ Leon Bankoff: Are the twin circles of Archimedes really twins? In: Mathematics Magazine. MAA 1974. Vol. 47, No. 4, 214–218.
- ↑ Clayton W. Dodge, Thomas Schoch, Peter Y. Woo, Paul Yiu: Those Ubiquitous Archimedean Circles. In: Mathematics Magazine. MAA 1999, No. 72, 202–213 (Faksimile siehe Weblinks).
Literatur
- Donald J. Albers, Gerald L. Alexanderson: Fascinating Mathematical People: Interviews and Memoirs. Princeton University Press 2011.
Fachartikel (Auswahl)
- 1954 über den Arbelos:
Leon Bankoff: A Mere Coincidence. In: Mathematics Newsletter. Los Angeles City College 1954; reprinted in College Math. Journal 1992, No. 23, 106.
- 1962 über das Morley-Dreieck:
Leon Bankoff: A Simple Proof of the Morley Theorem. In: Mathematics Magazine. MAA 1962, Vol. 35, No. 4., 223–224.
- 1973 über den „asymmetrischen Propeller“ (als Koautor von Paul Erdős hat Bankoff die Erdős-Zahl 1):
Leon Bankoff, Paul Erdős, Murray Klamkin: The asymmetric propeller. In: Mathematics Magazine. MAA 1973. No. 46, 270–272.
- 1974 über die Zwillingskreise des Archimedes:
Leon Bankoff: Are the twin circles of Archimedes really twins? In: Mathematics Magazine. MAA 1974. Vol. 47, No. 4, 214–218.
- 1987 über den Schmetterlingssatz:
Leon Bankoff: The Metamorphosis of the Butterfly Problem. In: Mathematics Magazine. MAA 1987, Vol 60, No. 4, 195–210.
- 1994 über den Arbelos:
Leon Bankoff: The Marvelous Arbelos. In: The Lighter Side of Mathematics. MAA 1994, 247–253.
Weblinks
Alle hier angegebenen Quellen sind in englischer Sprache.