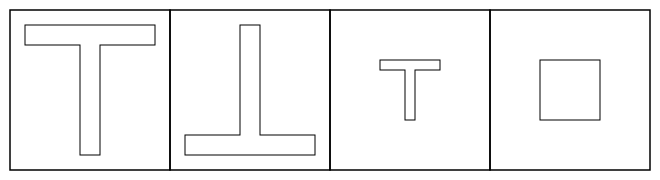
Kongruenz (Geometrie)
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Carlos VeloLahir(1909-11-15)15 November 1909Cartelle, SpanyolMeninggal21 September 1996(1996-09-21) (umur 78)Mexico City, MeksikoPekerjaanSutradaraProduserPenulis naskahTahun aktif1934–1983 Carlos Velo (15 November 1909 – 1...

English Hakka-Dictionary (英客字典) PengarangFr. MarsecanoNegaraTaiwanBahasaBahasa Inggris, bahasa HakkaDiterbitkan1958PenerbitKuangchi PressHalaman635 English Hakka-Dictionary adalah kamus Inggris - Hakka yang dikompilasikan oleh Fr. Marsecano, tokoh agama Katolik asal Italia yang mengabdi di Taiwan dari tahun 1955-2000.[1] National Taichung University of Science and Technology telah memindai kamus ini dan memungkinkannya diakses secara terbuka di internet. Penamaan dalam bahasa ...

Ticketmaster Entertainment, Inc.JenisSubsidierIndustriLive EntertainmentDidirikan2 Oktober 1976; 47 tahun lalu (1976-10-02)Phoenix, Arizona, Amerika SerikatPendiriAlbert Leffler Peter Gadwa Jerry NelsonKantorpusatBeverly Hills, California, Amerika SerikatWilayah operasiSeluruh duniaTokohkunciMichael Rapino (CEO) Jared Smith (Presiden Ticketmaster Global) Mark Yovich (Presiden Ticketmaster International) Amy Howe (Presiden Ticketmaster North America) ProdukTeknologi pertiketanPenjualan ti...

Untuk kegunaan lain, lihat Baby Blues (disambiguasi). Baby BluesPoster rilis teatrikalSutradaraAndibachtiar YusufProduserRaam PunjabiSkenarioImam DartoCeritaBalraj SinghPemeran Vino G. Bastian Aurélie Moeremans Penata musikStevesmith Music ProductionSinematograferAsep KalilaPenyuntingTeguh RaharjoPerusahaanproduksi Maxstream Original MVP Pictures DistributorMaxstreamTanggal rilis 24 Maret 2022 (2022-03-24) Durasi100 menitNegaraIndonesiaBahasaBahasa Indonesia Baby Blues adalah film...

Jalan Vincent di Cessnock Cessnock adalah sebuah kota di Wilayah Hunter dari New South Wales, Australia. Letak Cessnock berjarak sekitar 52 kilometer dari Newcastle bila melalui perjalanan darat ke arah barat. Artikel bertopik Australia ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan mengembangkannya.lbs
Kematian King John, dalam sebuah produksi tahun 1865 dari drama tersebut di Drury Lane Theatre, London The Life and Death of King John adalah sebuah drama sejarah Shakespearean karya William Shakespeare. Karya tersebut mendramatisir masa pemerintahan John, Raja Inggris (memerintah 1199–1216), putra dari Henry II dari Inggris dan Eleanor dari Aquitaine dan ayah dari Henry III dari Inggris. Pranala luar Cari tahu mengenai King John (drama) pada proyek-proyek Wikimedia lainnya: Gamba...

Papirus 66, bagian dari kumpulan Papirus Bodmer Papirus Bodmer (bahasa Inggris: Bodmer Papyri) adalah sekumpulan 22 naskah papirus yang ditemukan di Mesir pada tahun 1952. Dinamakan menurut Martin Bodmer yang membelinya. Naskah-naskah papirus tersebut memuat potongan-potongan dari Perjanjian Lama dan Perjanjian Baru, sastra Kristen kuno, karya-karya Homer dan Menander. Naskah tertua, P66 bertarikh ~ tahun 200. Naskah-naskah papirus ini disimpan pada Bibliotheca Bodmeriana, di Cologny, Swi...

Chinese painter (1895–1953) In this Chinese name, the family name is Xu. Xu Beihong徐悲鴻Born(1895-07-19)19 July 1895Yixing, Jiangsu, ChinaDied26 September 1953(1953-09-26) (aged 58)Beijing, ChinaNationalityChineseOther namesJu PéonKnown forOil painting, Chinese ink paintingChinese nameTraditional Chinese徐悲鴻Simplified Chinese徐悲鸿TranscriptionsStandard MandarinHanyu PinyinXú BēihóngWade–GilesHsü Pei-hung Xu Beihong (Chinese: 徐悲鴻; Wade–Gile...

2008 Detroit Indy Grand PrixRace details16th round of the 2008 IndyCar Series seasonDateAugust 31, 2008Official nameDetroit Indy Grand Prix presented by FirestoneLocationDetroit, MichiganCourseTemporary street circuit2.07 mi / 3.33 kmDistance87 laps180.09 mi / 289.82 kmScheduled Distance90 laps186.30 mi / 299.82 kmWeatherTemperatures reaching up to 86 °F (30 °C); wind speeds up to 10.2 miles per hour (16.4 km/h)[1]Pole positionDriverScott Dixon (Chip Ganass...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

本表是動態列表,或許永遠不會完結。歡迎您參考可靠來源來查漏補缺。 潛伏於中華民國國軍中的中共間諜列表收錄根據公開資料來源,曾潛伏於中華民國國軍、被中國共產黨聲稱或承認,或者遭中華民國政府調查審判,為中華人民共和國和中國人民解放軍進行間諜行為的人物。以下列表以現今可查知時間為準,正確的間諜活動或洩漏機密時間可能早於或晚於以下所歸�...

Jason ClermontNo. 82Born: (1978-05-24) May 24, 1978 (age 45)Regina, Saskatchewan, CanadaCareer informationCFL statusNationalPosition(s)SBHeight6 ft 2 in (188 cm)Weight227 lb (103 kg)UniversityReginaHigh schoolRobert UsherCFL draft2002, Round: 1, Pick: 4Drafted byBC LionsCareer historyAs player2002–2008BC Lions2009–2011Saskatchewan Roughriders Career highlights and awardsCFL All-Star2007CFL West All-Star2004, 2007Awards 2002 CFL Most O...

Speakers of the National Assembly of Tanzania Politics of Tanzania Constitution Human rights Government President (list) Samia Suluhu Hassan Vice-President Philip Mpango Prime Minister (list) Kassim Majaliwa Legislature Speaker Job Ndugai Judiciary Chief Justice of Tanzania Ibrahim Hamis Juma Court of Appeal High Court Elections Recent elections General: 201520202025 Political parties Subdivisions Regions Districts Foreign relations Ministry of Foreign Affairs Minister: Stergomena Tax Diploma...

In matematica, più precisamente nella teoria della probabilità, un processo stocastico (o processo aleatorio) è la versione probabilistica del concetto di sistema dinamico. Un processo stocastico è un insieme ordinato di funzioni reali di un certo parametro (in genere il tempo) che gode di determinate proprietà statistiche. In generale è possibile identificare questo processo come una famiglia con un parametro di variabili casuali reali X ( t ) {\displaystyle X(t)} rappresentanti le tra...

Seks dan hukum Isu sosial Usia dewasa · Penyensoran Sunat · Pornografi Pelanggaran tertentu(Dapat bervariasi sesuai dengan yurisdiksi) Perselingkuhan · Pemikatan anak Pornografi anak-anak · Pelacuran anak Hubungan sedarah · Pelacuran Pedofilia · Pemerkosaan (Pemerkosaan statutori · Pemerkosaan dalam pernikahan) Sexting · Pelecehan seksual terhadap anak Perbudakan seksual · Pelecehan seksual Zoofili...

Dante e Virgilio incontrano Forese Donati (Gustave Doré) Forese Donati (Firenze, 1250 circa – Firenze, luglio 1296) è stato un poeta italiano. Amico di Dante Alighieri, è con costui protagonista della celebre tenzone e dei canti XXIII e XXIV del Purgatorio. Indice 1 Biografia 1.1 Famiglia 1.2 Il matrimonio e la morte 2 Citazioni nella letteratura 2.1 La dantesca Tenzone con Forese Donati 2.2 I Canti XXIII e XXIV del Purgatorio 3 Note 4 Bibliografia 5 Altri progetti 6 Collegamenti esterni...

هذه مقالة غير مراجعة. ينبغي أن يزال هذا القالب بعد أن يراجعها محرر؛ إذا لزم الأمر فيجب أن توسم المقالة بقوالب الصيانة المناسبة. يمكن أيضاً تقديم طلب لمراجعة المقالة في الصفحة المخصصة لذلك. (نوفمبر 2020) رقصة سيف الباسك Mer Dandiya، رقصة سيف تؤديها مجتمعات سوراشترا رقصات السيف هي رق...

Questa pagina sull'argomento geografia sembra trattare argomenti unificabili alla pagina Repubblica dell'Artsakh. Puoi contribuire unendo i contenuti in una pagina unica. Segui i suggerimenti del progetto di riferimento. Voce principale: Repubblica dell'Artsakh. La repubblica dell'Artsakh era suddivisa principalmente in sette regioni più la capitale Step'anakert, città a statuto speciale, le quali costituivano la suddivisione amministrativa di primo livello. Indice 1 Regioni 2 Comunit...

Turkish newspaper BugünTypeDaily newspaperFormatBerlinerOwner(s)Koza İpek HoldingEditorErhan Başyurt[1]Founded6 September 2005[1]Political alignmentGülenismLanguageTurkishCeased publication29 February 2016CityIstanbulCountryTurkeyCirculation110,000 (2013)[2]Websitewww.bugun.com.tr [dead link]Media of TurkeyList of newspapers Bugün (English: Today) was a Turkish daily newspaper. It was established in 2005. Columnists and journalists working for it have incl...

Former monarchy in Europe Lippe-Brake was a county during the 17th century, located in Lippe, Germany, and ruled by a branch of the House of Lippe. History Otto, Count of Lippe-Brake The county was created in 1621 for Otto, Count of Lippe-Brake, second son of Count Simon VI of Lippe who had passed away in 1613. Otto's elder brother Simon VII ruled Lippe-Detmold, while his younger brother Philip I, Count of Schaumburg-Lippe inherited Lippe-Alverdissen and founded the Schaumburg-Lippe branch fo...