Hyperbolisches Volumen
|
Read other articles:

Untuk pemain sepak bola Amerika Serikat, lihat Jose White. José White pada 1856 José Silvestre White Lafitte (17 Januari 1836, di Matanzas, Kuba – 12–15 Maret 1918, Paris, Prancis), juga dikenal sebagai Joseph White, adalah seorang pemain biola dan komponis Kuba-Prancis. Ayahnya Don Carlos White adalah orang Spanyol dan ibunya adalah Afrika-Kuba.[1] Referensi ^ José Silvestre White, Afro-Cuban Composer, Violinist & Professor, Afri-Classical.com. Pranala luar https:/...

2020 film by the Pierce Brothers The WretchedTheatrical release posterDirected byThe Pierce BrothersWritten byThe Pierce BrothersProduced by Chang Tseng Ed Polgardy Brett Pierce Drew Pierce Travis Cultreri Starring John-Paul Howard Piper Curda Zarah Mahler Kevin Bigley Gabriela Quezada Bloomgarden Richard Ellis Blane Crockarell Jamison Jones Azie Tesfai CinematographyConor MurphyEdited byTerry YatesMusic byDevin BurrowsProductioncompanyLittle RunwayDistributed byIFC MidnightRelease dates July...

Welcome to Waikiki 2Poster promosiNama alternatifWaikiki 2Laughter in Waikiki 2Go Go Waikiki 2Woohoo Waikiki 2Hangul으라차차 와이키키 2 GenreKomediDitulis olehKim Ki-hoSong Ji-eunSong Mi-soSeo Dong-bumSutradaraLee Chang-minPemeranLee Yi-kyungKim Seon-hoShin Hyun-sooMoon Ga-youngAhn So-heeKim Ye-wonNegara asalKorea SelatanBahasa asliKoreaJmlh. episode16ProduksiProduserBaek Chang-juPark Jin-hyungPark Jun-seoDurasi70 menitRumah produksiC-JeS EntertainmentDrama House & JTBC ContentDi...

1010 ← 1011 → 1012素因数分解 3×337二進法 1111110011三進法 1101110四進法 33303五進法 13021六進法 4403七進法 2643八進法 1763十二進法 703十六進法 3F3二十進法 2AB二十四進法 1I3三十六進法 S3ローマ数字 MXI漢数字 千十一大字 千拾壱算木 1011(千十一、一〇一一、せんじゅういち)は自然数、また整数において、1010の次で1012の前の数である。 性質 1011は合成数であり、約数は 1, ...

Neo-grotesque sans-serif typefaceFor the country referred to as the same name in Latin, see Switzerland.For other uses, see Helvetica (disambiguation).Not to be confused with Helvetia, the national personification of Switzerland.HelveticaCategorySans-serifClassificationNeo-grotesque[1]Designer(s)Max MiedingerEduard HoffmannFoundryHaas'sche Schriftgiesserei (Basel)Date released1957Re-issuing foundriesMergenthaler Linotype CompanyDesign based onAkzidenz-GroteskVariationsHelvetica Insera...

English cricketer Dominic CorkCork in September 2009Personal informationFull nameDominic Gerald CorkBorn (1971-08-07) 7 August 1971 (age 52)Newcastle-under-Lyme, Staffordshire, EnglandNicknameCorky, Half-PintHeight188 cm (6 ft 2 in)BattingRight-handedBowlingRight-arm fast-mediumRoleAll-rounderRelationsGreg Cork (son)International information National sideEnglandTest debut (cap 572)22 June 1995 v West IndiesLast Test9 September 2002 v India...

Chinese merchant and politician of the Qin state (291–235 BCE) Lü BuweiChancellor of QinIn office251 BCE – 235 BCEMonarchsKing Zhuangxiang of Qin Ying ZhengSucceeded byLi Si Personal detailsBorn291 BCEDied235 BCE (aged 55–56)OccupationMerchant, politician In this Chinese name, the family name is Lü (呂). Lü BuweiTraditional Chinese呂不韋Simplified Chinese吕不韦TranscriptionsStandard MandarinHanyu PinyinLǚ BùwéiGwoyeu RomatzyhLeu BuhweiWade–GilesLü3 Pu4-wei2...
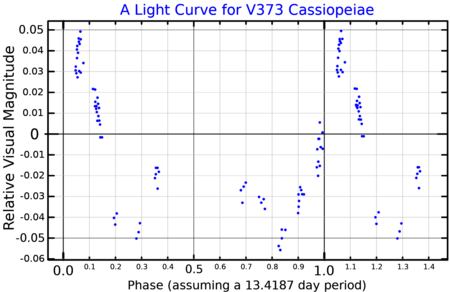
Star system in the constellation Cassiopeia V373 Cassiopeiae V373 Cassiopeiae (center) in optical light. The bright yellow star to the upper right of V373 Cas is ρ Cas. Observation dataEpoch J2000 Equinox J2000 Constellation Cassiopeia Right ascension 23h 55m 33.83878s[1] Declination +57° 24′ 43.8057″[1] Apparent magnitude (V) 6.03[2] Characteristics Spectral type B0.5II + B4III/V[2] ...

Disambiguazione – Se stai cercando altri significati, vedi Mirone (disambigua). Discobolo Lancellotti. Copia in marmo del II secolo d.C. (provenienza: scavi dell'Esquilino, 1871), da originale bronzeo di Mirone datato al 450 a.C. circa. Roma, Museo nazionale romano, Palazzo Massimo, Collezione Lancellotti. Mirone di Elèutere (Eleutere, ... – V secolo a.C.) è stato uno scultore greco antico attivo tra il 480 e il 440 a.C. Fu uno dei più elogiati rappresentanti dello stile severo. Indic...

مسجد الجراد التاريخيمعلومات عامةالمنطقة الإدارية منطقة حائلالمنطقة التاريخية بلدة مغيضة التاريخيةالبلد السعوديةأبرز الأحداثبداية التشييد 1279 هـ , 1862 م تعديل - تعديل مصدري - تعديل ويكي بيانات مسجد الجراد؛ هو مسجد تاريخي يقع في منطقة حائل، المملكة العربية السعودية. المو...

Questa voce sull'argomento politici paraguaiani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Bernardino Caballero 9º Presidente del ParaguayDurata mandato4 settembre 1880 –25 novembre 1886 Vice presidenteJuan Antonio Jara PredecessoreCándido Bareiro SuccessorePatricio Escobar Dati generaliPartito politicoPartido Colorado (Paraguay) Bernardino Caballero de Añasco y Melgarejo (Ybycuí, 20 maggio 1839 – Asunción, 26 feb...

Emeritus professor of English and a Tolkien scholar Michael Foster (December 28, 1946 - April 12, 2023[1]), known as Mike Foster, was an emeritus professor of English and a Tolkien scholar. In 1978 he pioneered the teaching of Tolkien studies at university level. Biography [My students] wanted a class on Tolkien alone. So in 1977, ... I took a petition signed by fifteen students requesting such a course to my department chairman, and he agreed to schedule Lit. 116: Special Studies: J....

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Heihuquan – news · newspapers · books · scholar · JSTOR (February 2007) (Learn how and when to remove this message) Hēi-Hǔ-Quán黑虎拳Also known asBlack Tiger FistCountry of originChinaParenthoodNorthern Shaolin Kung FuOlympic sportNo Part of a series onCh...

Bendera Finlandia dalam keadaan setengah tiang karena serangan Norwegia 2011 pada 24 Juli 2011. Hari berkabung nasional adalah hari yang ditandai dengan kegiatan berduka dan peringatan yang dilaksanakan oleh suatu negara untuk menandai kematian atau pemakaman seorang figur terhormat dari negara tersebut, atau memperingati tragedi besar lainya yang signifikansinya berpengaruh terhadap negara. Ini dilaksanakan sebagai bentuk penghormatan terakhir bagi yang telah meninggal dunia atas jasa-jasany...

2018 American sex comedy film The Pact (2018 film) redirects here. For the Spanish horror thriller film, see The Pact (2018 Spanish film). BlockersTheatrical release posterDirected byKay CannonWritten by Brian Kehoe Jim Kehoe Produced by Evan Goldberg Seth Rogen James Weaver Jon Hurwitz Hayden Schlossberg Chris Fenton Starring Leslie Mann Ike Barinholtz John Cena CinematographyRuss AlsobrookEdited byStacey SchroederMusic byMateo MessinaProductioncompanies Universal Pictures[1] Good Un...

2019 video game For the first game in the series, see Race Driver: Grid. 2019 video gameGridDeveloper(s)CodemastersPublisher(s)CodemastersSeriesGridEngineEgoPlatform(s)Microsoft WindowsPlayStation 4Xbox OneStadiaReleaseWindows, PS4, Xbox One11 October 2019Stadia19 November 2019Amazon Luna20 October 2020Genre(s)RacingMode(s)Single-player, multiplayer Grid is a 2019 racing video game developed and published by Codemasters for Microsoft Windows, PlayStation 4, and Xbox One in October 2019, and f...

Railway station in Kagoshima, Kagoshima Prefecture, Japan Hiroki Station広木駅General informationLocationHiroki, Kagoshima, Kagoshima(鹿児島県鹿児島市広木)JapanOperated byJR KyushuLine(s)Kagoshima Main LineHistoryOpened2009; 15 years ago (2009) Hiroki Station (広木駅, Hiroki-eki) is a railway station on the Kagoshima Main Line operated by Kyushu Railway Company in Kagoshima, Kagoshima, Japan. The station opened on March 14, 2009.[1] Lines Kyushu R...

2009 video game 2009 video gameRig'n'RollNorth American cover artDeveloper(s)SoftLab-NSKPublisher(s)1C Company (Russia & UK)Rondomedia (Germany)Cenega (Poland & CZE)Focus Multimedia (UK)THQ[1] (North America)Designer(s)Igor BelagoPlatform(s)Microsoft WindowsReleaseBoxed/retailRU: November 27, 2009CZE: May 7, 2010GER: May 22, 2010POL: June 11, 2010UK: June 25, 2010NA: July 14, 2010[1]Digital downloadRU: November 18, 2009EN: April 16, 2010GER: May 20, 2010Genre(s)Truck s...

Close-fitting necklace For other uses, see Choker (disambiguation). Princess Maria Annunciata of Bourbon-Two Sicilies Filigree choker of Our Lady of Porta Vaga A choker is a close-fitting necklace worn around the neck, typically 14 inch to 16 inch in length. Chokers can be made of a variety of materials, including velvet, plastic, beads, latex, leather, metal, such as silver, gold, or platinum, etc. They can be adorned in a variety of ways, including with sequins, studs, or a pendant. America...

Questa voce o sezione sull'argomento società calcistiche italiane non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. US Massese 1919 SSDCalcio Apuani, Zebre, Bianconeri Segni distintiviUniformi di gara Casa Trasferta Colori sociali Bianco, nero InnoAvanti Massese Avanti[1] Dati societariCittàMassa Nazione Italia ConfederazioneUEFA Federazione...


























