Harold Stark
| |||||||||||||
Read other articles:

Hotel Borobudur JakartaHotel BorobudurLua error in Modul:Mapframe at line 384: attempt to perform arithmetic on local 'lat_d' (a nil value).Jaringan hotelDiscovery Hotels and ResortsInformasi umumLokasi Jakarta, IndonesiaAlamatJl. Lapangan Banteng Selatan No.1, Ps. Baru, Sawah Besar, Kota Jakarta Pusat, Daerah Khusus Ibukota Jakarta 10710Koordinat-6.172089576721191, 106.835166931152340Pembukaan1974PemilikDiscovery Hotels and ResortsData teknisJumlah lantai18 termasuk 3 lantai eksekutifInforma...

Stadium on the main campus of Rutgers University SHI StadiumThe Birthplace of College FootballSHI Stadium during a football game in 2006SHI StadiumLocation within Middlesex County, New JerseyShow map of Middlesex County, New JerseySHI StadiumSHI Stadium (New Jersey)Show map of New JerseySHI StadiumSHI Stadium (the United States)Show map of the United StatesFormer namesRutgers Stadium (1994–2011)High Point Solutions Stadium (2011–2017)HighPoint.com Stadium (2018–2019)Address1 Scarlet Kni...

Azerbaijan Artikel ini adalah bagian dari seri Politik dan KetatanegaraanRepublik Azerbaijan Konstitusi Presiden: Ilham Aliyev Wakil Presiden: Mehriban Aliyeva Kepresidenan Perdana Menteri: Artur Rasizade Kabinet Menteri Majelis Nasional Ketua: Sahiba Gafarova Partai politik Pemilihan umum Pembagian administratif Hubungan luar negeri Hak Asasi Manusia Lihat pula Negara lainnya Atlas lbs Konstitusi Azerbaijan atau Undang-Undang Negara Azerbaijan (bahasa Azerbaijan: Azərbaycan konstitusiya...
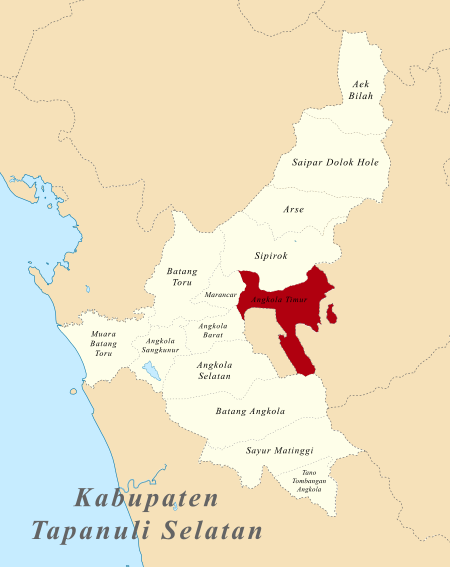
Angkola TimurKecamatanKantor Kecamatan Angkola TimurPeta lokasi Kecamatan Angkola TimurNegara IndonesiaProvinsiSumatera UtaraKabupatenTapanuli SelatanPemerintahan • CamatDarwin DalimunthePopulasi (2020)[1] • Total21.294 jiwa • Kepadatan91/km2 (240/sq mi)Kode pos22733Kode Kemendagri12.03.03 Kode BPS1203070 Luas235,16 km²Desa/kelurahan13 desa2 kelurahan Angkola Timur adalah sebuah kecamatan yang berada di Kabupaten Tapanuli Selatan, pr...

The HonourablePeter DuttonMPDutton pada 2022 Pemimpin OposisiPetahanaMulai menjabat 30 Mei 2022Perdana MenteriAnthony AlbaneseWakilSussan LeyPendahuluAnthony AlbanesePenggantiPetahanaPemimpin Partai Liberal ke-15PetahanaMulai menjabat 30 Mei 2022WakilSussan LeyPendahuluScott MorrisonPengganti Jabatan menteri Menteri PertahananMasa jabatan30 Maret 2021 – 23 Mei 2022Perdana MenteriScott MorrisonWakilAndrew HastiePendahuluLinda ReynoldsPenggantiRichard MarlesPemimpin Dewan Per...

1980 Olympic ice hockey tournament Ice hockey at the 1980 Winter OlympicsTournament detailsHost country United StatesVenue(s)Olympic Fieldhouse,Olympic ArenaLake Placid, New YorkDatesFebruary 12–24, 1980Teams12Final positionsChampions United States (2nd title)Runner-up Soviet UnionThird place SwedenFourth place FinlandTournament statisticsGames played35Goals scored308 (8.8 per game)Scoring leader(s) Milan Nový (15 points)&...

Gubernatorial elections were held in Massachusetts November 9, 1846 1846 Massachusetts gubernatorial election ← 1845 November 9, 1846 (1846-11-09) 1847 → Nominee George N. Briggs Isaac Davis Samuel E. Sewall Party Whig Democratic Liberty Popular vote 54,813 33,199 9,997 Percentage 53.78% 32.58% 9.81% Governor before election George N. Briggs Whig Elected Governor George N. Briggs Whig Elections in Massachusetts General 1942 1944 1946 1948 1950 ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: New Dimension! Crayon Shinchan the movie: Battle of Supernatural Powers ~Flying Sushi~ – news · newspapers · books · scholar · JSTOR (February 2024) (Learn how and when to remove this message) 2023 Japanese animated film New Dimension! Crayon Shinchan the movie...

穆罕默德·达乌德汗سردار محمد داود خان 阿富汗共和國第1任總統任期1973年7月17日—1978年4月28日前任穆罕默德·查希爾·沙阿(阿富汗國王)继任穆罕默德·塔拉基(阿富汗民主共和國革命委員會主席團主席) 阿富汗王國首相任期1953年9月7日—1963年3月10日君主穆罕默德·查希爾·沙阿 个人资料出生(1909-07-18)1909年7月18日 阿富汗王國喀布尔逝世1978年4月28日(...

Endangered Tupian language of Brazil Not to be confused with the Anambé of Ehrenreich. AnambéNative toBrazilRegionPará, Cairari RiverEthnicity130 Anambé (2000)[1]Native speakers6 (2006)[1]Language familyTupian Tupi–GuaraníXinguAnambéLanguage codesISO 639-3aanGlottologanam1249ELPAnambé of CairaríAnambé is classified as Critically Endangered by the UNESCO Atlas of the World's Languages in Danger Anambé, or more specifically Anambe of Cairari, is a possibly ...

Samoa Tula’iB. Indonesia: Samoa, Bangkit!Bendera SamoaLagu kebangsaan SamoaPenulis lirikSauni Iiga KuresaKomponisSauni Iiga KuresaPenggunaan1962Sampel audioberkasbantuan Sampel audioSamoa Tula’iberkasbantuan Samoa Tula’i adalah lagu kebangsaan Samoa. Lirik (Samoa, Bangkit) dan lagu digubah oleh Sauni Iiga Kuresa. Samoa mengambil Samoa Tula'i sebagai lagu kebangsaannya saat merdeka dari Selandia Baru pada tahun 1962. Lirik Samoa, tula'i ma sisi ia lau fu'a, lou pale lea; Samoa...

Air warfare branch of Oman's military RAFO redirects here. For a Romanian oil refinery, see RAFO Oneşti. Royal Air Force of Omanسلاح الجو السلطاني عمانSilāḥ al-Jaww as-Sulṭāniy ‘UmānBadge of the Royal Air Force of OmanFounded1959; 65 years ago (1959)Country OmanTypeAir forceRoleAerial warfarePart ofSultan of Oman's Armed ForcesCommandersCommander-in-ChiefSultan Haitham bin TariqCommander of the Air ForceAir Vice-Marshal Khamis bin Hamm...

جون مالكوفيتش (بالإنجليزية: John Malkovich) جون مالكوفيتش، أغسطس 2009 معلومات شخصية اسم الولادة جون غافن مالكوفيتش الميلاد 9 ديسمبر 1953 (العمر 70 سنة)كرستوفر، إلينوي، الولايات المتحدة الإقامة كامبريدج مواطنة الولايات المتحدة العرق أمريكيون صرب [لغات أخرى][1]...

Zeppelin-StaakenStato Germania Fondazione1916 a Staaken Fondata daFerdinand von Zeppelin Chiusura1920 Sede principaleGotha SettoreAeronautico Prodottiaerei civili e militari Modifica dati su Wikidata · Manuale La Zeppelin-Staaken (citata anche come Zeppelin Werke Staaken o Zeppelin-Werke GmbH) era una azienda aeronautica tedesco imperiale la cui sede originale era situata a Gotha, nella Turingia. Nasce infatti dall'iniziativa di Ferdinand von Zeppelin che ideò il concetto del ...

Living in the SkyPosterNama lain空に住む (Sora ni sumu)SutradaraShinji AoyamaProduser Tetsuhiro Inoue Hiroaki Saito Ditulis olehMasato OdakeSkenario Shinji Aoyama Chihiro Ikeda BerdasarkanLiving in the Sky by Masato OdakePemeranMikako TabePenata musikHiroyuki NagashimaSinematograferMio NakajimaPenyuntingGenta TamakiPerusahaanproduksi KAZUMO HIGH BROW CINEMA DistributorAsmik AceTanggal rilis 23 Oktober 2020 (2020-10-23) Durasi118 menit[1]NegaraJepangBahasaJepang Li...

UdineseNama lengkapUdinese Calcio SpAJulukanBianconeri (Putih Hitam), Zebrette (Zebra Kecil)Berdiri Daftar 30 November 1896; 127 tahun lalu (30 November 1896), sebagai Società Udinese di Ginnastica e Scherma.5 Juli 1911; 113 tahun lalu (1911-07-05), sebagai Associazione del Calcio Udine1919; 105 tahun lalu (1919), sebagai Associazione Sportiva Udinese1925; 99 tahun lalu (1925), sebagai Associazione Calcio Udinese1978; 46 tahun lalu (1978), sebagai Udinese Calcio Stad...

Chip EngellandBiographieNaissance 9 mai 1961 (63 ans)Pacific PalisadesNationalité américaineFormation Palisades Charter High School (en)Université DukeActivités Joueur de basket-ball, entraîneur de basket-ballPériode d'activité 1984-1991Autres informationsTaille 1,93 mPoids 79,4 kgSport Basket-ballÉquipes Duke Blue Devils (1979-1983)San Miguel Beermen (en)Nuggets de DenverPistons de DétroitSpurs de San AntonioSun Kings de Yakamamodifier - modifier le code - modifier Wikidata Art...

Leonora CarringtonLahir(1917-04-06)6 April 1917Clayton-le-Woods, Lancashire, InggrisMeninggal25 Mei 2011(2011-05-25) (umur 94)Mexico City, MeksikoDikenal atasLukisanTulisanGerakan politikSurrealismeSuami/istriRenato LeducEmerico Chiki WeiszAnakGabriel dan Pablo WeiszSitus webwww.leocarrington.com Penghargaan(2005) National Prize for Arts and Sciences (en) (1986) Women's Caucus for Art Lifetime Achievement Award (en) Officer of the Order of the British Empire (en) Leonora Carrington OBE ...

Village in Nišava, SerbiaGornji Adrovac, SerbiaVillageGornji Adrovac, SerbiaCoordinates: 43°29′53″N 21°37′51″E / 43.49806°N 21.63083°E / 43.49806; 21.63083CountrySerbiaDistrictNišavaMunicipalityAleksinacPopulation (2002) • Total134Time zoneUTC+1 (CET) • Summer (DST)UTC+2 (CEST) Gornji Adrovac (Serbian: Горњи Адровац) is a village in the municipality of Aleksinac, Serbia. According to the 2002 census, the village ha...

Highway in the United States U.S. Highway 264US 264 in red, US 264 Alt. in blue, US 264 Bus. in Belhaven in pinkRoute informationAuxiliary route of US 64Maintained by NCDOTLength215.7 mi[1] (347.1 km)Existed1932–presentTouristroutes Pamlico Scenic BywayMajor junctionsWest end I-87 / I-440 / US 64 / US 64 Bus. in Raleigh Major intersections I-540 near Knightdale US 64 near Zebulon I-95 / I-587 / I-795 near Wilson I-587 ...






