Read other articles:

ALTAIR Radar. Salah satu jenis radar jarak jauh yang digunakan untuk mendeteksi objek di luar angkasa Radar 36D6 (Tin Shield) Radar ini adalah jenis radar pertahanan udara untuk mendeteksi objek terbang seperti pesawat atau peluru kendali. Radar (yang dalam bahasa Inggris merupakan singkatan dari radio detection and ranging, yang berarti deteksi dan penjarakan radio) adalah suatu sistem gelombang elektromagnetik yang berguna untuk mendeteksi, mengukur jarak dan membuat map benda-benda seperti...

Disambiguazione – Se stai cercando l'omonima famiglia mantovana, vedi Agnelli (famiglia mantovana). Questa voce o sezione sull'argomento storia di famiglia è priva o carente di note e riferimenti bibliografici puntuali. Sebbene vi siano una bibliografia e/o dei collegamenti esterni, manca la contestualizzazione delle fonti con note a piè di pagina o altri riferimenti precisi che indichino puntualmente la provenienza delle informazioni. Puoi migliorare questa voce citando le fonti pi...

Canadian soccer player (born 1977) Paul Stalteri Stalteri captaining Canada in 2008Personal informationFull name Paul Andrew Stalteri[1]Date of birth (1977-10-18) October 18, 1977 (age 46)[2]Place of birth Etobicoke, Ontario, CanadaHeight 5 ft 11 in (1.80 m)[2]Position(s) Wing-back, midfielderTeam informationCurrent team Canada (assistant)Youth career1992–1995 Malton BulletsCollege careerYears Team Apps (Gls)1995–1996 Clemson Tigers Senior caree...

1844 American novel by Maturin Murray Ballou Fanny Campbell, protagonist of the 1844 novel Fanny Campbell, the Female Pirate by Maturin Murray Ballou Fanny Campbell, the Female Pirate Captain: A Tale of the Revolution is an 1844 American novel by Maturin Murray Ballou, about a woman who goes to sea to rescue her fiancé and becomes commander of a pirate ship. The popularity of its heroine continued long after the book was published, with some writers publishing accounts of Fanny Campbell as i...

John Baldacci 73º Governatore del MaineDurata mandato8 gennaio 2003 - 5 gennaio 2011 PredecessoreAngus King SuccessorePaul LePage Membro della Camera dei Rappresentanti - Maine, distretto n.2Durata mandato3 gennaio 1995 – 3 gennaio 2003 PredecessoreOlympia Snowe SuccessoreMike Michaud Dati generaliPartito politicoDemocratico Firma John Elias Baldacci (Bangor, 30 gennaio 1955) è un politico statunitense, è stato Governatore del Maine. Appartenente al Partito Democratico, è...

Cet article est une ébauche concernant le Kazakhstan. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. District de Jangueldy Sceau Noms Nom kazakh Жангелді ауданы Nom russe Administration Pays Kazakhstan Oblys Kostanaï Centre administratif Torgaï Démographie Population 15 690 hab. (2009) Géographie Coordonnées 49° 49′ nord, 63° 43′ est Localisation Situation...

Pour les articles homonymes, voir Barboure (homonymie). La BarboureRuisseau des Lochères La Barboure à Marson-sur-Barboure. Caractéristiques Longueur 13,8 km [1] Bassin 69 km2 [1] Bassin collecteur La Seine Débit moyen (Naix-aux-Forges) Nombre de Strahler 2 Régime pluvial océanique Cours Source source du Franois · Localisation Naives-en-Blois · Altitude 329 m · Coordonnées 48° 39′ 13″ N, 5° 31′ 41″ E Confluence l'Ornain · Loca...

Fruit from which the majority of the original water content has been removed Dried fruitDried fruit and nuts on a platterOriginMediterranean, Mesopotamia, India, specifically south IndiaUsePreservation of fruit for sweeteners or snacksProductionEarliest: Dates and raisinsBiggest modern: RaisinsNutritionDried fruit have most of the nutrition value of fresh fruit Dried fruit is fruit from which the majority of the original water content has been removed either naturally, through sun drying, or ...

Religious explanation For other approaches to the study of the universe in its totality, see Cosmology. For other approaches to the origin of the Universe, see Cosmogony. God rests with his creation. Julius Schnorr von Carolsfeld 1860 Religious cosmology is an explanation of the origin, evolution, and eventual fate of the universe from a religious perspective. This may include beliefs on origin in the form of a creation myth, subsequent evolution, current organizational form and nature, and e...

International sports competition where competitors represent their nation For the flagship association football competition World Cup, see FIFA World Cup. For the flagship cricket competition World Cup, see ICC Cricket World Cup. For a more exhaustive list, see List of world cups. For World championships, see List of world sports championships and List of world championships in mind sports. For the song by IShowSpeed, see World Cup (song). The Alpine Skiing World Cup consists of a series of c...

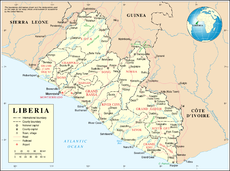
United Nations resolution adopted in 2002 UN Security CouncilResolution 1395LiberiaDate27 February 2002Meeting no.4,481CodeS/RES/1395 (Document)SubjectThe situation in LiberiaVoting summary15 voted forNone voted againstNone abstainedResultAdoptedSecurity Council compositionPermanent members China France Russia United Kingdom United StatesNon-permanent members Bulgaria Cameroon Colombia Guinea Ireland Mauritius Mexico Norwa...

Sligo SligeachTownGedung Dewan KelurahanSligoSligo di IrlandiaTampilkan peta IrelandSligoSligo (Eropa)Tampilkan peta EropaKoordinat: 54°16′00″N 8°29′00″W / 54.2667°N 8.4833°W / 54.2667; -8.4833Koordinat: 54°16′00″N 8°29′00″W / 54.2667°N 8.4833°W / 54.2667; -8.4833CountryIrlandiaProvinsiConnachtCountyCounty SligoParlemen EropaMidlands–North-WestLuas[1] • Total10,3 km2 (40 sq mi)Ketinggi...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 %   获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

  لمعانٍ أخرى، طالع عدد عشري. نظام عد عشريمعلومات عامةالأساس 10[1] nonary (en) undecimal (en) تعديل - تعديل مصدري - تعديل ويكي بيانات جزء من سلسلة مقالات حولأنظمة العد نظام العد الهندي العربي نظام العد الهندي العربي عربية عربية مشرقية بنغالية غورموخية Indian سنهالية تاميليّة باليّ...

1908 Serbian parliamentary election ← 1906 31 May 1908 1912 → All 160 seats in the National Assembly81 seats needed for a majorityTurnout70.0% Party Leader % Seats +/– NRS Nikola Pašić 43.62 84 −7 SRS Ljubomir Stojanović 31.07 48 +1 NS–SNS – 16.29 17 +16 National Stojan Ribarac 4.08 7 −8 Progressive Stojan Novaković 2.94 3 −2 SSDP Dragiša Lapčević 0.76 1 0 This lists parties that won seats. See the complete results below. Prime Minister before Prime Mi...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Bethesda Hospital Ambur – news · newspapers · books · scholar · JSTOR (October 2011) This ar...

Field-equations in general relativity Einstein equation redirects here. For the equation E = m c 2 {\displaystyle E=mc^{2}} , see Mass–energy equivalence. General relativity G μ ν + Λ g μ ν = κ T μ ν {\displaystyle G_{\mu \nu }+\Lambda g_{\mu \nu }={\kappa }T_{\mu \nu }} Introduction HistoryTimelineTests Mathematical formulation Fundamental concepts Equivalence principle Special relativity World line Pseudo-Riemannian manifold Phenomen...

American private equity firm Symphony Technology GroupCompany typePrivate companyHeadquartersMenlo Park, California, U.S.[1]Websitewww.stg.com Symphony Technology Group (STG) is an American private equity firm based in Menlo Park, California.[1] Its Managing Partner and Chief Investment Officer is William Chisholm who co-founded the firm with Bryan Taylor and Dr. Romesh Wadhwani in 2002. Investments The company has investments in the following companies:[2] Connexity (...

Public university in Leicester, England De Montfort redirects here. For other uses, see Montfort (disambiguation). De Montfort University LeicesterCoat of ArmsFormer namesLeicester School of Art Leicester Colleges of Art and Technology Leicester PolytechnicMottoLatin: Excellentia et studiumMotto in EnglishExcellence and ZealTypePublicEstablished1870; 154 years ago (1870) 1992 – university statusEndowment£2.56 million (2022)[1]Budget£234.6 million (2021–22)...

Shorthand way of determining whether a given number is divisible by a fixed divisor A divisibility rule is a shorthand and useful way of determining whether a given integer is divisible by a fixed divisor without performing the division, usually by examining its digits. Although there are divisibility tests for numbers in any radix, or base, and they are all different, this article presents rules and examples only for decimal, or base 10, numbers. Martin Gardner explained and popularized thes...