Gemeinsame Geschäftsordnung der Bundesministerien
| |||||||||||||||||||
Read other articles:

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (July 2013) (Learn how and when to remove this template message) William Sewell (1781–1853) was the second principal of the London Veterinary College, succeeding Edward Coleman who died in 1839. Life Grave of William Sewell in Highgate Cemetery Sewell was the son of an Essex farmer and of Quaker descent. At ag...

Stasiun Mertoyudan Mertoyudan+343 m Stasiun Mertoyudan, 2018.Lokasi Jalan Mayor Jenderal Bambang SugengMertoyudan, Mertoyudan, Magelang, Jawa TengahIndonesiaKoordinat7°31′1.8005″S 110°13′35.1707″E / 7.517166806°S 110.226436306°E / -7.517166806; 110.226436306Koordinat: 7°31′1.8005″S 110°13′35.1707″E / 7.517166806°S 110.226436306°E / -7.517166806; 110.226436306Ketinggian+343 mOperator Kereta Api IndonesiaDaerah Operasi VI Y...

Bagian dari Alkitab KristenPerjanjian LamaYosua 1:1 pada Kodeks Aleppo Taurat Kejadian Keluaran Imamat Bilangan Ulangan Sejarah Yosua Hakim-hakim Rut 1 Samuel 2 Samuel 1 Raja-raja 2 Raja-raja 1 Tawarikh 2 Tawarikh Ezra Nehemia Ester Puisi Ayub Mazmur Amsal Pengkhotbah Kidung Agung Kenabian Besar Yesaya Yeremia Ratapan Yehezkiel Daniel Kecil Hosea Yoël Amos Obaja Yunus Mikha Nahum Habakuk Zefanya Hagai Zakharia Maleakhi Deuterokanonika Tobit Yudit Tambahan Ester 1 Makabe 2 Makabe Kebijaksanaa...

Cet article est une ébauche concernant le droit français. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Article 46 de la Constitution du 4 octobre 1958 Données clés Présentation Pays France Langue(s) officielle(s) Français Type Article de la Constitution Adoption et entrée en vigueur Législature IIIe législature de la Quatrième République française Gouvernement Charles de Gaulle (3e) Promulgation 4...

Bagian dari seriIslam Rukun Iman Keesaan Allah Malaikat Kitab-kitab Allah Nabi dan Rasul Allah Hari Kiamat Qada dan Qadar Rukun Islam Syahadat Salat Zakat Puasa Haji Sumber hukum Islam al-Qur'an Sunnah (Hadis, Sirah) Tafsir Akidah Fikih Syariat Sejarah Garis waktu Muhammad Ahlulbait Sahabat Nabi Khulafaur Rasyidin Khalifah Imamah Ilmu pengetahuan Islam abad pertengahan Penyebaran Islam Penerus Muhammad Budaya dan masyarakat Akademik Akhlak Anak-anak Dakwah Demografi Ekonomi Feminisme Filsafat...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (سبتمبر 2021) يان هيكر (بالألمانية: Jan Hecker) مناصب سفير ألمانيا لدى الصين في المنصب24 أغسطس 2021 – 6 سبتمبر 2021 كليمنس فون جويتز [لغات أخرى] معلوم...

العلاقات الأفغانية البوروندية أفغانستان بوروندي أفغانستان بوروندي تعديل مصدري - تعديل العلاقات الأفغانية البوروندية هي العلاقات الثنائية التي تجمع بين أفغانستان وبوروندي.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولت�...

Canadian soccer team Football clubBurlington SCFull nameBurlington Soccer ClubNickname(s)BayhawksFounded1962StadiumHaber CentreCapacity1000Head CoachDarren Tilley (men) Neil Wilson (women)LeagueLeague1 Ontario2022League1 Ontario, 17th (men)League1 Ontario, 20th (women)WebsiteClub website Current season Burlington Soccer Club is a Canadian semi-professional soccer club based in Burlington, Ontario that plays in League1 Ontario. History The club was founded in 1962 under the name Burlington Po...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Voce principale: Forlì Football Club. AC ForlìStagione 1982-1983 Sport calcio Squadra Forlì Allenatore Angelo Becchetti Presidente Giovanni Bianchi Serie C118º nel girone A (retrocesso in Serie C2) Coppa Italia Serie CFase eliminatoria a gironi Maggiori presenzeCampionato: Cossaro, Della Monica (30) Miglior marcatoreCampionato: Pin (5) StadioTullo Morgagni 1981-1982 1983-1984 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti l'Associazione ...

Series of novels by Robert Shea and Robert Anton Wilson The Illuminatus! Trilogy First collected edition, 1984AuthorsRobert SheaRobert Anton WilsonCover artistCarlos Victor Ochagavia (1975 paperbacks)CountryUnited StatesLanguageEnglishGenresatire, science fictionPublisherDell PublishingPublication date1975 (individual volumes); 1984 (collected edition)Media typePrint (hardback & paperback)Pages805 pages (paperback collected edition)ISBN1-56731-237-3 (hardback collected edition),...
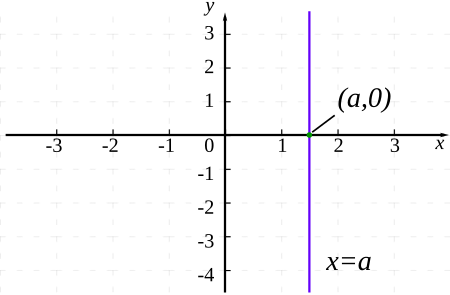
Equation that does not involve powers or products of variables Two graphs of linear equations in two variables In mathematics, a linear equation is an equation that may be put in the form a 1 x 1 + … + a n x n + b = 0 , {\displaystyle a_{1}x_{1}+\ldots +a_{n}x_{n}+b=0,} where x 1 , … , x n {\displaystyle x_{1},\ldots ,x_{n}} are the variables (or unknowns), and b , a 1 , … , a n {\displaystyle b,a_{1},\ldots ,a_{n}} are the coefficients, which are often real numbers. The ...
Census-designated place in Texas, United StatesFabens, TexasCensus-designated placeLocation of Fabens, TexasCoordinates: 31°30′18″N 106°9′15″W / 31.50500°N 106.15417°W / 31.50500; -106.15417CountryUnited StatesStateTexasCountyEl PasoArea • Total4.35 sq mi (11.26 km2) • Land4.32 sq mi (11.20 km2) • Water0.02 sq mi (0.06 km2)Elevation3,615 ft (1,102 m)Population (...

2022年內華達州州長選舉 ← 2018 2022年11月8日 2026 → 获提名人 喬·隆巴爾多 史蒂夫·西索拉克 政党 共和黨 民主党 民選得票 497377 481991 得票率 48.8% 47.3% 縣市結果西索拉克: 50–60% 60–70% 70–80% 80–90% 隆巴爾多: 40–50% 50–60% 选前州長 史蒂夫·西索拉克...

Peta infrastruktur dan tata guna lahan di Komune Grisy-sur-Seine. = Kawasan perkotaan = Lahan subur = Padang rumput = Lahan pertanaman campuran = Hutan = Vegetasi perdu = Lahan basah = Anak sungaiGrisy-sur-SeineNegaraPrancisArondisemenProvinsKantonBray-sur-SeineAntarkomuneCommunauté de communes du Canton de Bray-sur-SeinePemerintahan • Wali kota (2008-2014) Jean-Claude Jegoudez • Populasi1102Kode INSEE/pos77218 / 2 ...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

Trans-Neptunian object @ 89AU 2014 UZ2242014 UZ224 imaged by ALMADiscovery[1]Discovered byDavid Gerdes et al.Discovery siteCerro Tololo Obs.Discovery date19 August 2014DesignationsMPC designation2014 UZ224Alternative designationsDeeDee (nickname)Minor planet categoryTNO[2] · SDO[3]p-DP[4]Orbital characteristics[2]Epoch 31 May 2020 (JD 2459000.5)Uncertainty parameter 5 · 6[5]Observation arc12.0...

Parliamentary constituency in the United Kingdom since 1983 Doncaster CentralBorough constituencyfor the House of CommonsBoundary of Doncaster Central in South Yorkshire for the 2010 general electionLocation of South Yorkshire within EnglandCountySouth YorkshireElectorate70,446 (December 2019)[1]Major settlementsDoncasterCurrent constituencyCreated1983Member of ParliamentRosie Winterton (Labour)SeatsOneCreated fromDoncaster and Don Valley[2] Doncaster Central is a constitu...

Characterization of how many integers are prime This article uses technical mathematical notation for logarithms. All instances of log(x) without a subscript base should be interpreted as a natural logarithm, also commonly written as ln(x) or loge(x). In mathematics, the prime number theorem (PNT) describes the asymptotic distribution of the prime numbers among the positive integers. It formalizes the intuitive idea that primes become less common as they become larger by precisely quantifying...

German politician and surgeon (1883–1965) Maxim Zetkin in 1953 Maxim Zetkin (1 August 1883, Paris – 19 August 1965, East Berlin) was a German politician and surgeon. Biography Maxim Zetkin was born in Paris in 1883 to Ossip and Clara Zetkin. Two years later his younger brother Kostja was born. After attending a high school in Stuttgart, Zetkin studied medicine in Munich from 1902 to 1908. He received his doctorate there in 1909. In 1902 Zetkin joined the SPD; in 1917 he joined USPD and in...