Faktorraum
|
Read other articles:

American politician (1896–1965) Olin D. JohnstonUnited States Senatorfrom South CarolinaIn officeJanuary 3, 1945 – April 18, 1965Preceded byWilton E. HallSucceeded byDonald S. Russell98th Governor of South CarolinaIn officeJanuary 19, 1943 – January 2, 1945LieutenantRansome J. WilliamsPreceded byRichard M. JefferiesSucceeded byRansome J. WilliamsIn officeJanuary 15, 1935 – January 17, 1939LieutenantJoseph E. HarleyPreceded byIbra C. BlackwoodSucceeded byBurn...

TopolinoLogoStato Italia Linguaitaliano PeriodicitàMensile (1949-1952)Quindicinale (1952-1960)Settimanale (dal 1960) Generefumetto Formato12,5 × 18[1] cm FondatoreMario Gentilini Fondazione7 aprile 1949 Inserti e allegatiEdizioni speciali e gadget vari Sedevia Lampedusa, 13/C Milano EditoreArnoldo Mondadori Editore (1949-1988)The Walt Disney Company Italia (dal 1988)Panini Comics (dal 2013) Tiratura512 538[2] (gennaio - dicembre 2022) Diffusione cartacea338 31...

Danilo Pereira Danilo Pereira con la maglia del Porto nel 2015 Nazionalità Portogallo Altezza 188 cm Peso 83 kg Calcio Ruolo Centrocampista, difensore Squadra Paris Saint-Germain Carriera Giovanili 2002-2005 Arsenal 722005-2008 Estoril Praia2008-2010 Benfica2010-2011 Parma Squadre di club1 2011→ Arīs Salonicco5 (2)2011-2012 Parma5 (0)2012-2013→ Roda JC31 (1)[1]2013-2015 Marítimo57 (4)2015-2020 Porto135 (15)2020- Paris ...

Fangshan 房山区DistrikPabrik Petrokimia YanshanLokasi Distrik Fangshan di BeijingKoordinat (Pemerintah Fangshan): 39°44′56″N 116°08′36″E / 39.7488°N 116.1434°E / 39.7488; 116.1434Koordinat: 39°44′56″N 116°08′36″E / 39.7488°N 116.1434°E / 39.7488; 116.1434NegaraRepublik Rakyat TiongkokMunisipalitasBeijingDivisi daerah administrasi kota praja8 subdistrik14 kota praja6 daerah administrasi kota prajaLuas • ...

Type of occupational stress Burn out and Burn Out redirect here. For other uses, see Burnout (disambiguation). Not to be confused with Occupational burning. Medical conditionOccupational burnoutOther namesBurn-out, exhaustion disorder, neurastheniaA person who is experiencing psychological stressSpecialtyPsychology SymptomsEmotional exhaustion, depersonalization, reduced personal accomplishment,[1][2] fatigue[3]Differential diagnosisMajor depressive disorder The I...

French association football club based in Guingamp This article is about the men's football club. For the women's football team, see En Avant Guingamp (women). Football clubGuingampFull nameEn Avant GuingampNickname(s)Les GuingampaisLes Costarmoricains (The Costamoricans)Les Rouge et Noir (The Red and Blacks)L'En-Avant[1]Short nameEAGFounded1912; 112 years ago (1912)GroundStade de RoudourouCapacity19,033PresidentFrédéric LegrandHead coachStéphane DumontLeagueLigue...

Open access train operating co-operative Go-op logo Go-op (full name Go-op Cooperative Ltd,[1]) is an open access train operating company which is currently proposing to operate a service between Taunton and Swindon, via Westbury. It aims to become the first cooperatively owned train operating company in the United Kingdom,[2] to improve access to the public transport infrastructure through open access rail services linking main lines to smaller market towns, and co-ordinating...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

Katakan SejujurnyaAlbum studio karya Christine PanjaitanDirilis1987GenrePopLabelLolypop RecordsProduserRinto HarahapKronologi Christine Panjaitan Frida (1985)Frida1985 Katakan Sejujurnya (1987) Perasaan (1987)Perasaan1987 Katakan Sejujurnya adalah album musik karya Christine Panjaitan. Dirilis pada tahun 1987. Hits single-nya adalah Katakan Sejujurnya. Daftar lagu KATAKAN SEJUJURNYA, Rinto Harahap NIKMATNYA CINTA, Andy Nasution LELAH, Billy Eden DURI CINTA DALAM DADA, Dadang S. Manaf IDOL...

Untuk gubernur pra-Mongol Hulagu di Persia pada pertengahan abad ke-13, lihat Arghun Aqa. Untuk desa di Iran, lihat Arghun, Iran. Untuk kota di Afghanistan, lihat Urgun. Arghun ᠠᠷᠭᠤᠨKhanSebuah lukisan yang menggambarkan Arghun (berdiri, menggendong putranya Ghazan) di bawah payung kerajaan. Di sebelahnya adalah ayahnya Abaqa duduk di atas kuda.Berkuasa1284–7 Maret 1291PendahuluTekuderPenerusGaykhatuAyahAbaqaPasanganQuthluq KhatunUruk KhatunTodai KhatunSaljuk KhatunBulughan KhatunQ...

LGBT rights in BelizeBelizeStatusLegal since 2016[1]Gender identityNoMilitaryNoDiscrimination protectionsSexual orientation protections[2]Family rightsRecognition of relationshipsNo recognition of same-sex couplesAdoptionNo Lesbian, gay, bisexual, and transgender (LGBT) persons in Belize face legal challenges not experienced by non-LGBT citizens, although attitudes have been changing in recent years. Same-sex sexual activity was decriminalized in Belize in 2016, when the Supr...
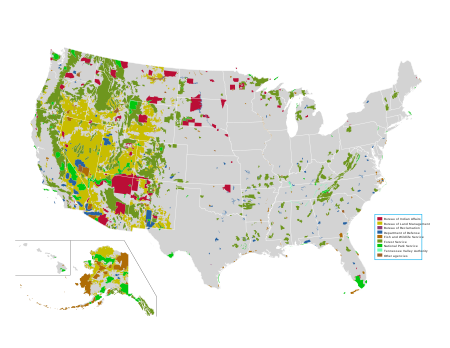
This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The examples and perspective in this article deal primarily with the United States and do not represent a worldwide view of the subject. You may improve this article, discuss the issue on the talk page, or create a new article, as appropriate. (December 2018) (Learn how and when to remove this message) This article needs additional citations...

Street in the City of London, England 51°31′01″N 0°05′52″W / 51.5170°N 0.0978°W / 51.5170; -0.0978 An office building on Little Britain. St Botolph's Aldersgate on Little Britain Little Britain is a street in the City of London running from St. Martin's Le Grand in the east to West Smithfield in the west. It is situated in the Aldersgate and Farringdon Within wards. Postman's Park is also bounded by Little Britain. Historically, Little Britain referred to a...

فيليز موستار تأسس عام 1922 البلد البوسنة والهرسك الدوري دوري البوسنة والهرسك الممتاز الموقع الرسمي الموقع الرسمي الطقم الرسمي الطقم الأساسي الطقم الاحتياطي تعديل مصدري - تعديل نادي فيليز موستار لكرة القدم (بالبوسنوية: Fudbalski Klub Velež Mostar) هو ناد بوسني لكرة قدم م�...

Caribbean and Latin American dish This article is about the savoury maize dumpling. For pastries, pies, and cakes, see pastel (food). This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (April 2012) (Learn how and when to remove this message) PastelesPuerto Rican pastelesTypeDumpling Pasteles (Spanish pronunciation: [pasˈteles]; singular pastel), also pas...

Jacques Lacan Información personalNombre completo Jacques Marie Émile LacanNacimiento 13 de abril de 1901 III Distrito de París (Francia) Fallecimiento 9 de septiembre de 1981 (80 años)VI Distrito de París (Francia) Causa de muerte Cáncer colorrectal Sepultura Guitrancourt Nacionalidad FrancesaReligión Católico FamiliaCónyuge Marie-Louise Blondin (1934-1941)Sylvia Bataille (1953-1981) Hijos Judith Miller EducaciónEducación Doctor en Medicina Educado en Collège Stanislas ...

Disambiguazione – Se stai cercando l'omonimo album, vedi Storia di un italiano (album). Storia di un italianoPaeseItalia Anno1979-1986 Generedocumentario, costume Lingua originaleitaliano RealizzazioneConduttoreAlberto Sordi Rete televisivaRai 2 Modifica dati su Wikidata · Manuale Storia di un italiano è stato un programma televisivo ideato e condotto da Alberto Sordi, andato in onda su Rai 2 la domenica in prima serata[1], e trasmesso in più edizioni tra il 1979 e...

Inferior third of the medial border of the humerus Medial supracondylar ridgeLeft humerus. Anterior view. (Medial supracondylar ridge on side at bottom left, but not labeled.)DetailsIdentifiersLatincrista supracondylaris medialisTA98A02.4.04.016TA21199FMA75076Anatomical terms of bone[edit on Wikidata] The inferior third of the medial border of the humerus is raised into a slight ridge, the medial supracondylar ridge (or medial supracondylar line), which becomes very prominent below; it pr...
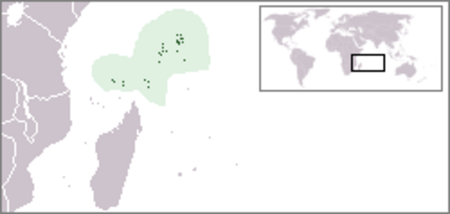
LGBTQ rights in SeychellesSeychellesStatusLegal since 2016Gender identityNoMilitaryNoDiscrimination protectionsSexual orientation protections in employment (see below)Family rightsRecognition of relationshipsNoAdoptionNo Lesbian, gay, bisexual, and transgender (LGBT) people in Seychelles face legal challenges not experienced by non-LGBTQ residents. Same-sex sexual activity has been legal since 2016, and employment discrimination on the basis of sexual orientation is banned in Seychelles, mak...

Person raised by one or more deaf people For the film, see CODA (2021 film). A child of deaf adult, often known by the acronym CODA, is a person who was raised by one or more deaf parents or legal guardians. Ninety percent of children born to deaf adults can hear normally,[1] resulting in a significant and widespread community of CODAs around the world, although whether the child is hearing, deaf, or hard of hearing has no effect on the definition. The acronym KODA (kid of deaf adult)...








![{\displaystyle [v]:=v+U:=\{v+u\mid u\in U\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/840a6fb8965e08b66d990a28ba4b980ed218a497)

![{\displaystyle V/U:=\{[v]\mid v\in V\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82a29a0c365cecbd72ac13f3eb5b4d76e6beacbe)
![{\displaystyle [v_{1}]+[v_{2}]=[v_{1}+v_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6f04ad77f545f15f464133a452d05a91aaf7cb2)
![{\displaystyle \lambda \cdot [v]=[\lambda v]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37a0d490d8912b98166e93345411b3ca750cb0c1)


![{\displaystyle \pi \colon \;V\to V/U,\;v\mapsto [v]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f6aed82860793afb18f985eaf362ea53b2dc673)










![{\displaystyle [v]\mapsto p(v)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b17be410710bc2263c6f7889670e97065a37ce6)





