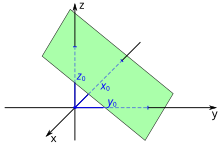
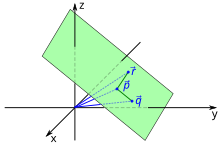
Ebenengleichung
|
Read other articles:

Tumpukan staples yang biasa digunakan di rumah dan di kantor Staples atau isi kokot[1] adalah sebuah pengencang dua arah, biasanya terbuat dari metal dan berbentuk seperti U yang digunakan untuk menyatukan dua atau beberapa bahan. Staples yang berukuran besar bisa digunakan bersama dengan palu atau staple gun untuk menyatukan atap, kayu, kardus dan kegunaan kelas berat lain. Staples yang lebih kecil biasanya dipasangkan dengan stapler untuk menyatukan lembaran-lembaran kertas. Tidak s...

Ichikawa 市川町Kota kecil BenderaLambangLokasi Ichikawa di Prefektur HyōgoNegara JepangWilayahKansaiPrefektur HyōgoDistrikKanzakiPemerintahan • Wali kotaTakezō IwamiLuas • Total82,7 km2 (31,9 sq mi)Populasi (Oktober 1, 2015) • Total12.300 • Kepadatan148,7/km2 (385/sq mi)Zona waktuUTC+09:00Kode pos679-2392Simbol • PohonFagaceae • BungaHelianthus annuusNomor telepon0790-26...

Part of a series onBritish law Acts of Parliament of the United Kingdom Year 1801 1802 1803 1804 1805 1806 1807 1808 1809 1810 1811 1812 1813 1814 1815 1816 1817 1818 1819 1820 1821 1822 1823 1824 1825 1826 1827 1828 1829 1830 1831 1832 1833 1834 1835 1836 1837 1838 1839 1840 1841 1842 1843 1844 1845 1846 1847 1848 1849 1850 1851 1852 1853 1854 1855 1856 1857 1858 1859 1860 1861 1862 1863 1864 1865 1866 1867 1868 1869 1870 1871 1872 1873 1874 1875 1876 1877 1878 ...

Wakil Bupati Bangka SelatanPetahanaDebby Vita Dewi, S.E.sejak 26 Februari 2021Masa jabatan5 tahunDibentuk2005Pejabat pertamaH. JamroSitus webbangkaselatankab.go.id Berikut ini adalah daftar Wakil Bupati Bangka Selatan dari masa ke masa. No Wakil Bupati Mulai Jabatan Akhir Jabatan Prd. Ket. Bupati 1 H.Jamro 2005 2010 1 Ir. Drs. H.Justiar NoerM.M., B.A.E. 2 Nursyamsu H. Alias 30 Agustus 2010 30 Agustus 2015 2 H.Jamro Tidak ada 31 Agustus 2015 13 Januari 2016 - Drs. H.H...

Peta lokasi India Timur. India Timur adalah wilayah di India yang terdiri dari negara bagian Benggala Barat, Bihar, Jharkhand, dan Orissa. Secara geografis, wilayah ini terbentang antara India Utara dan India Timur-Laut. Negara bagian Orissa dan Benggala Barat memiliki banyak kesamaan budaya dan bahasa dengan Bangladesh dan negara bagian Assam. Artikel bertopik geografi atau tempat India ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan mengembangkannya.lbs

RevelationsEpisode The X-FilesNomor episodeMusim 3Episode 11SutradaraDavid NutterPenulisKim NewtonKode produksi3X11Tanggal siar15 Desember 1995Durasi44 menitBintang tamu Kevin Zegers sebagai Kevin Kryder Sam Bottoms sebagai Michael Kryder Kenneth Welsh sebagai Simon Gates Michael Berryman sebagai Owen Jarvis Hayley Tyson sebagai Susan Kryder R. Lee Ermey sebagai Pendeta Patrick Findley[1] Kronologi episode ← Sebelumnya731 Selanjutnya →War of the Coprophages Revelati...

1966 studio album by The DeepPsychedelic MoodsStudio album by The DeepReleasedOctober 1966RecordedAugust 19–20, 1966StudioCameo-Parkway Studios, Philadelphia, PAGenre Psychedelic rock garage rock Length29:43LabelCameo-ParkwayProducerThe Deep, Mark BarkanThe Deep chronology Psychedelic Moods(1966) Psychedelic Psoul(1967) Psychedelic Moods is the debut album by the American psychedelic rock band, The Deep, and was released on Cameo-Parkway Records in October 1966 (see 1966 in music). ...

AwardOrder of Merit of the Republic of PolandOrder Zasługi Rzeczypospolitej PolskiejThe Grand Cross of Order of Merit of the Republic of PolandTypeFive grade orderAwarded forService in improving relations between nationsCountry PolandPresented bythe President of PolandStatusCurrently awardedEstablished10 April 1974 (Revised 16 October 1992)Order of Merit of the Republic of Poland ribbon PrecedenceNext (higher)Order of the Cross of IndependenceNext (lower)Cross of Valour The O...

U.S. House district for Oregon OR-5 redirects here. For Oregon Route 5, see Interstate 5 in Oregon. For Oregon's 5th district in the Oregon House of Representatives, see Oregon's 5th House district. For NATO rank OR-5, see Ranks and insignia of NATO armies enlisted. Oregon's 5th congressional districtOregon's 5th congressional district since January 3, 2023Representative Lori Chavez-DeRemerR–Happy ValleyArea5,362 sq mi (13,890 km2)Distribution80.34% urban19.66% ruralPop...

Women's liberal arts college in Northampton, Massachusetts.For the private liberal arts colleges in Geneva, New York, see Hobart and William Smith Colleges.Smith CollegeMottoἘν τῇ ἀρετῇ τὴν γνῶσιν (Greek)Motto in EnglishTo Virtue, Knowledge (2 Peter 1:5)[1]TypePrivate liberal arts women's collegeEstablished1871; 153 years ago (1871) (opened 1875; 149 years ago (1875))AccreditationNECHEAcademic affiliationCOFHESeven Siste...

Tupoutoʻa ʻUlukalalaPutra Mahkota TongaKelahiran17 September 1985 (umur 38)NukuʻalofaWangsaDinasti TupouNama lengkapSiaosi Manumataongo ʻAlaivahamamaʻo ʻAhoʻeitu Konstantin TukuʻahoAyahTupou VIIbuNanasipau'u Tuku'ahoPasanganSinaitakala FakafanuaAnakTaufaʻahau ManumataongoAgamaMethodis Siaosi Manumataongo ʻAlaivahamamaʻo ʻAhoʻeitu Konstantin Tukuʻaho[1] (lahir 17 September 1985) adalah anggota keluarga kerajaan Tonga dan Putra Mahkota Tonga. Tupoutoʻa ʻUlukalala me...

ChouillycomuneChouilly – Veduta LocalizzazioneStato Francia RegioneGrand Est Dipartimento Marna ArrondissementÉpernay CantoneÉpernay-2 TerritorioCoordinate49°01′N 4°01′E / 49.016667°N 4.016667°E49.016667; 4.016667 (Chouilly)Coordinate: 49°01′N 4°01′E / 49.016667°N 4.016667°E49.016667; 4.016667 (Chouilly) Superficie16,03 km² Abitanti1 019[1] (2009) Densità63,57 ab./km² Altre informazioniCod. postale51530 Fus...

坐标:43°11′38″N 71°34′21″W / 43.1938516°N 71.5723953°W / 43.1938516; -71.5723953 此條目需要补充更多来源。 (2017年5月21日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:新罕布什尔州 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

Closed station in Brighton, England Kemp TownA train at the station in 1952, viewed from the northGeneral informationLocationKemptown, Brighton & HoveEnglandGrid referenceTQ321041Platforms1Other informationStatusDisusedHistoryPre-groupingLondon, Brighton and South Coast RailwayPost-groupingSouthern Railway Southern Region of British RailwaysKey dates1869Station opened1 January 1917closed19 August 1919opened1933Station closed to passengersJune 1971Station closed to freight26 June 1971Speci...

English nobleman The Right HonorableThe Earl of ArundelPC(Ire)Born15 August 1608Died17 April 1652(1652-04-17) (aged 43)BuriedArundel Castle, Arundel, West Sussex, EnglandNoble familyHowardSpouse(s)Lady Elizabeth StuartIssue12, including:Thomas Howard, 5th Duke of NorfolkHenry Howard, 6th Duke of NorfolkLord Philip HowardLord Charles HowardLord Bernard HowardFatherThomas Howard, 14th Earl of ArundelMotherAlethea Talbot Henry Frederick Howard, 15th Earl of Arundel PC(Ire) (15 August 1608&#...

Chow Kit Chow Kit adalah suatu sub-daerah di tengah kota Kuala Lumpur, Malaysia. Ia berada di sekitar Jalan Chow Kit, Jalan Haji Thaib, Jalan Pantai, dan Jalan Tuanku Abdul Rahman. Nama kawasan ini diambil dari nama seorang penambang timah dan kanselor kota, Loke Chow Kit. Daerah ini juga dikenal sebagai Little Jakarta, karena banyak dihuni oleh para pendatang asal Indonesia.[1] Sebagian besar mereka adalah orang Minangkabau, Jawa, dan Aceh yang banyak membuka restoran serta berniaga ...

الرفع والسحب هما مكونان من إجمالي القوة الديناميكية الهوائية التي تعمل على طائرة أو طائرة. في الديناميكا الهوائية، نسبةالرفع إلى السحب (lift-to-drag ratio) أو نسبة إل/دي أ(L/D ratio) هي الرفع الناتجة عن جسم ديناميكي هوائي مثل مُنساب هوائي (aerofoil) أو طائرة، مقسومًا على السحب الديناميكي ال�...

Photo du large de Venise Liste des 43 communes de la ville métropolitaine de Venise, dans la région Vénétie, en Italie. Sommaire : Haut – A B C D E F G H I J K L M N O P Q R S T U V W X Y Z A Annone Veneto C Campagna Lupia Campolongo Maggiore Camponogara Caorle Cavallino-Treporti Cavarzere Ceggia Chioggia Cinto Caomaggiore Cona Concordia Sagittaria D Dolo E Eraclea F Fiesso d'Artico Fossalta di Piave Fossalta di Portogruaro Fossò G Gruaro J Jesolo M Marcon Martellago Meolo Mira Mi...

United States Indo-Pacific Command InformationDatum1947-idagLand Amerikas förenta staterFörsvarsgrenFörsvarsgrensövergripandeTypMilitärkommandoRollStilla havetOstasienIndienOceanienAntarktisHögkvarterCamp H.M. Smith, HawaiiSmeknamnINDOPACOM United States Indo-Pacific Command (USINDOPACOM), Förenta staternas stillahavskommando, är det försvarsgrensövergripande militärkommandot med ansvar att försvara och upprätthålla USA:s säkerhetspolitiska intressen i och kring stilla havet, o...