Teorie chaosu
|
Read other articles:

Primary federal legislation authorizing the creation of national banks in the US National Bank Act of 1863Long titleAn Act to provide a national currency, secured by a pledge of United States stocks, and to provide for the circulation and redemption thereof.Enacted bythe 37th United States CongressEffectiveFebruary 25, 1863CitationsStatutes at Large12 Stat. 665Legislative historyIntroduced in the SenatePassed the Senate on February 12, 1863 (23â21)Passed the House on Feb...

Puteri Indonesia 2007Tanggal3 Agustus 2007TempatJakarta Convention Center, Jakarta, IndonesiaPembawa acaraFerdi HasanNadia MulyaPengisi acaraGita GutawaUnguChristopher AbimanyuPenyiaranSCTVPeserta36[1]Tidak tampilNanggroe Aceh DarussalamKalimantan TengahPemenangPutri Raemawasti Jawa Timur← 20062008 →lbs Puteri Indonesia 2007 adalah kontes Puteri Indonesia yang ke-12. Malam grand final pemilihan Puteri Indonesia 2007 diselenggarakan di Jakarta ...

Ãtienne Tshisekedi Perdana Menteri ZaireMasa jabatan2 April 1997 â 9 April 1997PresidenMobutu Sese Seko PendahuluLÃĐon KengoPenggantiLikulia BolongoMasa jabatan15 August 1992 â 18 March 1993PresidenMobutu Sese Seko PendahuluJean Nguza Karl-i-BondPenggantiFaustin BirindwaMasa jabatan29 September 1991 â 1 November 1991PresidenMobutu Sese Seko PendahuluMulumba LukojiPenggantiBernardin Mungul Diaka Informasi pribadiLahir(1932-12-14)14 Desember 1932Kabeya Kamwanga...

Wonju ėėĢžMunicipal CityTranskripsi Korea âĒ HangulėėĢžė âĒ Hanjaåå·åļ âĒ Revised RomanizationWonju-si âĒ McCune-ReischauerWÅnju-si Lambang dari WonjuLokasi di Korea SelatanNegara Korea SelatanRegionGwandongPembagian administrasi1 eup, 8 myeon, 16 dongLuas âĒ Total867,63 km2 (33,499 sq mi)Populasi (2010) âĒ Total310.854 âĒ Kepadatan317/km2 (820/sq mi) âĒ Dialec...

Tour de France 2002Coureurs dans l'ascension du mont VentouxGÃĐnÃĐralitÃĐsCourse 89e Tour de FranceÃtapes 20Date 6 au 28 juillet 2002Distance 3 277,5 kmPays traversÃĐ(s) France, Luxembourg, AllemagneLieu de dÃĐpart LuxembourgLieu d'arrivÃĐe ParisÃquipes 21Partants 189Vitesse moyenne 39,88 km/hRÃĐsultatsVainqueur non attribuÃĐ[1]DeuxiÃĻme Joseba BelokiTroisiÃĻme Raimondas RumÅĄasClassement par points Robbie McEwenMeilleur grimpeur Laurent JalabertMeilleur jeune Ivan BassoMeill...

UNAMNama lengkapClub de Futbol Universidad Nacional ACJulukanPumasUniversitarios (Universities)Berdiri28 Agustus 1954; 69 tahun lalu (1954-08-28)StadionEstadio OlÃmpico Universitario(Kapasitas: 72,000)PemilikUNAMKetuaRodrigo Ares de PargaManajerMichelLigaLiga MXApertura 20183rd (Liguilla)Situs webSitus web resmi klub Kostum kandang Kostum tandang Kostum ketiga Musim ini Club de Futbol Universidad Nacional AC atau lebih dikenal sebagai Pumas de la UNAM, UNAM, dan Pumas, adalah sebua...

This list is incomplete; you can help by adding missing items. (September 2018) Part of a series onNazism Organizations Ahnenerbe Geheime Staatspolizei Deutsches Jungvolk Hitler Youth League of German Girls NSDÃB NSDStB NSRL NSFK NSKK NSF Nationalsozialistische Monatshefte Nazi Party Sturmabteilung (SA) Schutzstaffel (SS) History Early timeline National Socialist Program Hitler's rise to power Machtergreifung German rearmament Nazi Germany Religion in Nazi Germany Kirchenkampf Adolf Hitler'...

Railway station in Cheshire, England Lostock GralamView west towards Northwich and Chester in 2013General informationLocationLostock Gralam, Cheshire West and ChesterEnglandGrid referenceSJ690746Managed byNorthern TrainsPlatforms2Other informationStation codeLTGClassificationDfT category F2HistoryOpened1 January 1863Passengers2018/19 52,3062019/20 54,0082020/21 17,7442021/22 43,0122022/23 54,108 NotesPassenger statistics from the Office of Rail and Road Lostock Gralam railway station serves t...

British submarine For other ships with the same name, see HMS Ursula. HMS Ursula History United Kingdom NameHMS Ursula BuilderVickers Armstrong, Barrow-in-Furness Laid down19 February 1937 Launched16 February 1938 Commissioned20 December 1938 FateTransferred to Soviet Navy, 26 June 1944 Badge Soviet Union NameV-4 Acquired26 June 1944 FateReturned to UK, early 1950 and scrapped May 1950 General characteristics Class and typeU-class submarine Displacement Surfaced â 540 tons standard, 630 ton...

White LiePoster promosi untuk White LieGenreKeluarga, RomansaDitulis olehJo Eun-jungSutradaraBae Han-chun Lee Min-sooPemeranShin Eun-kyung Kim Hae-sook Kim Yu-seok Kim Tae-hyun Im Ji-eunNegara asalKorea SelatanBahasa asliKoreaJmlh. episode159ProduksiProduser eksekutifLee Dae-youngLokasi produksiKorea SelatanDurasi30 menit dari hari Senin hingga Jumat pukul 07:50 (WSK)Rilis asliJaringanMunhwa Broadcasting CorporationRilis1 Desember 2008 (2008-12-01) â10 Juli 2009 (2009-7-10) ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Badarka â news · newspapers · books · scholar · JSTOR (November 2018) (Learn how and when to remove this message) This article may need to be rewritten to comply with Wikipedia's quality standards. You can help. The talk page may contain suggestions. (November ...

La mummiaUna locandina artistica del film a cura di Matt BuschTitolo originaleThe Mummy Lingua originaleinglese Paese di produzioneStati Uniti d'America Anno1999 Durata120 min Rapporto2,35:1 Genereazione, fantastico, avventura RegiaStephen Sommers SoggettoStephen Sommers, Lloyd Fonvielle, Kevin Jarre SceneggiaturaStephen Sommers ProduttoreSean Daniel, James Jacks Produttore esecutivoKevin Jarre Casa di produzioneUniversal Pictures, Alphaville Films Distribuzione in italianoUnited Inte...

City in Kerman province, Iran Nezamabad, Kerman redirects here. For other places named Nezamabad or Nizamabad in Kerman province, see Nezamabad, Kerman (disambiguation). City in Kerman, IranNezamshahr Persian: ŲØļاŲ ØīŲØąCityNezamshahrCoordinates: 28°54âē54âģN 58°32âē58âģE / 28.91500°N 58.54944°E / 28.91500; 58.54944[1]CountryIranProvinceKermanCountyNarmashirDistrictRud AbPopulation (2016)[2] âĒ Total2,426Time zoneUTC+3:30 (I...

Biografi tokoh yang masih hidup ini tidak memiliki referensi atau sumber sehingga isinya tidak dapat dipastikan. Bantu memperbaiki artikel ini dengan menambahkan sumber tepercaya. Materi kontroversial atau trivial yang sumbernya tidak memadai atau tidak bisa dipercaya harus segera dihapus.Cari sumber: Amanda Dwi Arista â berita · surat kabar · buku · cendekiawan · JSTOR (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Amanda Dwi Aris...
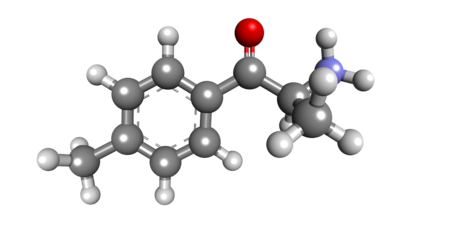
Stimulant designer drug 4-MethylcathinoneLegal statusLegal status DE: NpSG (Industrial and scientific use only) UK: Class B Identifiers IUPAC name 2-amino-1-(4-methylphenyl)propan-1-one CAS Number31952-47-3HCl: 6941-17-9PubChem CID414532ChemSpider367058UNIICY9HK59OK6CompTox Dashboard (EPA)DTXSID801032529 Chemical and physical dataFormulaC10H13NOMolar mass163.220 g·molâ13D model (JSmol)Interactive image SMILES CC1=CC=C(C=C1)C(=O)C(C)N InChI InChI=1S/C10H13NO/c1-7-3-5-9(6...

American adult animated sitcom Jeff & Some AliensGenreComedyCreated bySean DonnellyAlessandro MinoliBased onJeff & Some Aliensby Video LouStarringBrett GelmanAlessandro MinoliCountry of originUnited StatesOriginal languageEnglishNo. of seasons1No. of episodes10ProductionExecutive producersAlexander BulkleyCorey CampodonicoSean DonnellyAlessandro MinoliRunning time22 minutesProduction companiesShadowMachineComedy PartnersOriginal releaseNetworkComedy CentralReleaseJanuary 11 (2017...

La venere di Willendorf, una delle piÃđ celebri veneri callipige Le veneri paleolitiche sono piccole statue preistoriche raffiguranti donne con gli attributi sessuali molto pronunciati e ritratti con certo realismo (laddove il resto del corpo, a partire dal viso, ÃĻ raffigurato in modo assai approssimativo).[1] Vengono dette anche veneri steatopigie (dalle parole greche ÏÏÎÎąÏ, ÏÏÎÎąÏÎŋÏ, grasso, adipe, e ÏÏ ÎģÎŪ, natiche, quindi dalle grosse natiche) o callipigie (sempre da...

ããŪé įŪã§ãŊãæĨæŽãŪåķåšĶãŦãĪããĶ芎æããĶããūããį·čŦãŦãĪããĶãŊãäŋåĨãŧãģãŋãžãããčĶ§ãã ããã äŋåĨæ äŋåĨæ Health center æĨæŽãŪäŋåĨæãŪå°åģčĻå·čĻįŦ 1937åđī4æ5æĨčĻįŦč æģåķåŪ:æĨæŽå―æŋåš čĻį―Ū:åå°æđå Žå ąåĢä―čĻįŦå° æĨæŽįĻŪéĄ å ŽįæĐéĒæģįå°ä― å°æđæĐéĒįŪį įūį ãŪäšéēãčĄįãŪåäļãå°åä―æ°ãŪåĨåš·ãŪäŋæåĒéēå ŽįĻčŠ æĨæŽčŠäŋåĨæé· åå°æđå Žå ąåĢä―ãŪäŋåĨ...

Voce principale: Giochi della XXIX Olimpiade. Questa voce o sezione sugli argomenti Giochi olimpici e judo non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Judo aPechino 2008 Uomini Donne 60 kg 48 kg 66 kg 52 kg 73 kg 57 kg 81 kg 63 kg 90 kg 70 kg 100 kg 78 kg +100 kg +78 kg Le ...

Gal GadotŨŨ ŨŨŨŨŠGal Gadot pada tahun 2016Lahir30 April 1985 (umur 39)Petah Tikva, IsraelPekerjaanArtis, ModelTahun aktif2004 - sekarangTinggi178 cm (5 ft 10 in)[1]Suami/istriYaron Versano (m. 2008)Anak4 (2018) Time 100 Penghargaan Jupiter Gal Gadot (bahasa Ibrani: ŨŨ ŨŨŨŨŠ; lahir 30 April 1985) adalah artis dan model asal Israel yang pernah memerankan diri sebagai wonder woman di film Justice League.[2][3][4] Ia m...


