Přímka
|
Read other articles:

Gordon Banks OBE Banks pada tahun 2007Informasi pribadiNama lengkap Gordon Banks[1]Tanggal lahir (1937-12-30)30 Desember 1937Tempat lahir Abbeydale, Sheffield, InggrisTanggal meninggal 12 Februari 2019(2019-02-12) (umur 81)Tempat meninggal Stoke-on-Trent, InggrisTinggi 6 ft 1 in (1,85 m)Posisi bermain Penjaga gawangKarier junior1953 Millspaugh1953 Rawmarsh Welfare1953 Millspaugh1953–1958 ChesterfieldKarier senior*Tahun Tim Tampil (Gol)1958–1959 Chesterfield 23...

Arco di TraianoCiviltàRomana UtilizzoArco trionfale EpocaII secolo d.C. LocalizzazioneStato Italia ComuneAncona AmministrazioneVisitabileSi Mappa di localizzazione Modifica dati su Wikidata · ManualeCoordinate: 43°37′31″N 13°30′23.4″E / 43.625278°N 13.5065°E43.625278; 13.5065 L'arco di Traiano di Ancona è un arco trionfale attribuito ad Apollodoro di Damasco, fatto costruire nel II secolo d.C. dal Senato romano per esprimere la propria riconoscenza...
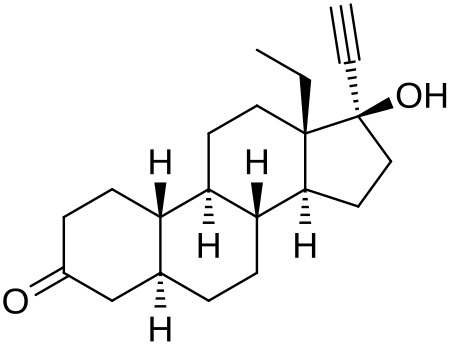
Chemical compound 5α-DihydrolevonorgestrelClinical dataOther names5α-Dihydrolevonorgestrel; 5α-DHLNG; 5α-LNGIdentifiers IUPAC name (5S,8R,9R,10S,13S,14S,17R)-13-Ethyl-17-ethynyl-17-hydroxy-1,2,4,5,6,7,8,9,10,11,12,14,15,16-tetradecahydrocyclopenta[a]phenanthren-3-one CAS Number78088-19-4PubChem CID9995794ChemSpider8171375UNII7Z4S6960I5Chemical and physical dataFormulaC21H30O2Molar mass314.469 g·mol−13D model (JSmol)Interactive image SMILES CC[C@]12CC[C@H]3[C@H]([C@@H]1CC[C@]2(C#C)...

Sumber referensi dari artikel ini belum dipastikan dan mungkin isinya tidak benar. Mohon periksa, kembangkan artikel ini, dan tambahkan sumber yang benar pada bagian yang diperlukan. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Waringin Sari TimurPekonNegara IndonesiaProvinsiLampungKabupatenPringsewuKecamatanAdiluwihLuas... km²Jumlah penduduk... jiwaKepadatan... jiwa/km² Untuk kegunaan lain, lihat Waringin Sari (disambiguasi). Waringin Sari Timur adalah pekon yan...

Eric DaneDane at the red carpet of the White House Correspondents' Association dinner, April 2008LahirEric William DanePekerjaanAktorTahun aktif1991 – sekarangSuami/istriRebecca Gayheart (2004-sekarang) Eric William Dane (lahir 9 November 1972) adalah aktor asal Amerika Serikat. Ia berperan dalam film Saved by the Bell, Marley & Me dan Valentine's Day. Filmografi Tahun Film Peran Catatan 1991 Saved by the Bell Tad Pogue TV episode (The Game) - uncredited 1993 The Wonder Years Bret...

NGC 72NGC 72, terletak tepat di atas NGC 71 dan di bawah NGC 71 adalah galaksi spiral NGC 70 (kanan) dan NGC 68 (kiri)Data pengamatan (J2000.0 epos)Rasi bintangAndromedaAsensio rekta 00j 18m 28.4dDeklinasi +30j 02m 26.5dPergeseran merah0.024213[1]Kecepatan radial helio7259 km/s[1]Jarak320-325 Mly[2][3]Magnitudo semu (V)13.5[4][2]Ciri-ciriJenisSb[5] Sbc[4] SA(rs)c[2]Ukuran180,000[...

American baseball executive and manager For other people named John McKeon, see John McKeon (disambiguation). Baseball player Jack McKeonMcKeon in 1983ManagerBorn: (1930-11-23) November 23, 1930 (age 93)South Amboy, New Jersey, U.S.Batted: RightThrew: RightMLB debutApril 6, 1973, for the Kansas City RoyalsLast MLB appearanceSeptember 28, 2011, for the Florida MarlinsMLB statisticsGames managed2,042Managerial record1,051–990Winning %.515 Teams Kansas City Royals...

County clerk of Cook County, Illinois Cook County ClerkIncumbentVacantsince April 7, 2024Term length4 yearsFormationMarch 1831 (appointed position)August 1837 (elected position) The Cook County Clerk is the clerk of county government in Cook County, Illinois. History The office of Cook County Clerk was established as an elected office with a four-year term in August 1837. Prior to this, from 1831 to 1837, the Clerk was appointed by the three Cook County Commissioners.[1] Officeho...

Indian psychiatrist and schizophreniz researcher Thara RangaswamyBornChennai, IndiaOccupationDoctorSpouseP. Srinivasan Thara Rangaswamy (born 25 May 1953) is a psychiatrist in India, the co-founder of an NGO called SCARF (Schizophrenia Research Foundation) based in Chennai, India. She is a researcher in schizophrenia and community mental health. In 2020, she received the SIRS Outstanding Clinical and Community Research Award of SIRS[1] (Schizophrenia International Research Society), a...

NK NewsURLwww.nknews.orgTipeSurat kabar daringPerdagangan ?YaRegistration (en)OpsionalLangueInggrisPemilikNK Consulting, Inc.Service entry (en)2011NegaraKorea Selatan Peringkat Alexa 112,862 (Oktober 2020[update])[1]KeadaanAktif NK News adalah situs web Amerika berbasis langganan yang menyediakan berita dan analisis tentang Korea Utara. Didirikan pada tahun 2011, berkantor pusat di Seoul, Korea Selatan dengan reporter di Washington, D.C. dan London.[2] Pelaporan d...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (نوفمبر 2019) هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحس...

Unguía FaultFalla UnguíaEtymologyUnguíaCoordinates08°03′27″N 77°07′23″W / 8.05750°N 77.12306°W / 8.05750; -77.12306Country Colombia PanamaRegionCaribbean, Pacific/ChocóStateChocóDariénCharacteristicsRangeSerranía del DariénPart ofCaribbean faultsLength139.9 km (86.9 mi)Strike356.3 ± 30DipWestDip angleLow to moderateDisplacement~0.2–1 mm (0.0079–0.0394 in)/yrTectonicsPlateCaribbean, North AndeanStatusInactiveTypeObl...

2001 2014 Élections municipales de 2008 à Toulouse Maire de Toulouse 9 et 16 mars 2008 Type d’élection Election municipale Postes à élire 68 conseillers municipaux Corps électoral et résultats Inscrits 242 961 Votants au 1er tour 137 283 Votes exprimés au 1er tour 129 724 Votes blancs au 1er tour 2 766 Votants au 2d tour 134 517 Votes exprimés au 2d tour 141 577 Votes blancs au 2d tour 5 206 Pierre Cohen – PS Avec vous, Toulouse avanc...

Cet article est une ébauche concernant le commerce. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Livreur de pizza sur une motocyclette. La livraison de pizza est un service dans lequel une pizzeria livre une pizza à un client situé dans une zone géographique proche directement à domicile ou au bureau. Pour cela un moyen de transport, classiquement une automobile ou un deux-roues, est utilisé. La command...

Instant messaging interface CentericqIRC chat windowDeveloper(s)Konstantin KlyaginInitial releaseAugust 1, 1999; 24 years ago (1999-08-01)[1]Final release4.21.0 (September 2, 2005; 18 years ago (2005-09-02)) [±] Written inC++Operating systemCross-platformAvailable inbg, cs, de, en, es, fr, hu, it, ms, nl, pl, pt, ro, ru, sv, uk, zh[2]TypeInstant messaging clientLicenseGPLWebsitethekonst.net/en/centericq Centericq is a text mode ...

Шалфей обыкновенный Научная классификация Домен:ЭукариотыЦарство:РастенияКлада:Цветковые растенияКлада:ЭвдикотыКлада:СуперастеридыКлада:АстеридыКлада:ЛамиидыПорядок:ЯсноткоцветныеСемейство:ЯснотковыеРод:ШалфейВид:Шалфей обыкновенный Международное научное наз...

For the Shaoxing era, see Emperor Gaozong of Song. For the former Shaoxing County, see Keqiao District. For the wine, see Shaoxing wine. Kuaiji redirects here. For other uses, see Kuaiji (disambiguation). Prefecture-level city in Zhejiang, People's Republic of ChinaShaoxing 绍兴市ShaohsingPrefecture-level cityLeft to right, top to bottom: Bazi Bridge over the Eastern Zhejiang Canal, Shaoxing cityscape, Didang subdistrict, Tishan Bridge, traditional houses in Zhuji.ShaoxingShow map of Zheji...

Classic hits radio station in Pittsfield, Massachusetts WUPESimulcast of WUPE-FM, North AdamsPittsfield, MassachusettsBroadcast areaBerkshire MountainsFrequency1110 kHzBrandingWhoopeeProgrammingFormatClassic hitsAffiliationsCompass Media NetworksPremiere NetworksUnited Stations Radio NetworksOwnershipOwnerTownsquare Media(Townsquare License, LLC)Sister stationsWBEC, WBEC-FM, WNAW, WSBS, WUPE-FMHistoryFirst air dateSeptember 9, 1971; 52 years ago (1971-09-09) (as WGRG)Former ...

Artikel ini memerlukan pemutakhiran informasi. Harap perbarui artikel dengan menambahkan informasi terbaru yang tersedia. Istilah kekaisaran atau Imperium menyiratkan perluasan kedaulatan suatu Negara atau Bangsa atas wilayah-wilayah eksternal, yang membawahi banyak negara, suku, dan bangsa untuk membentuk suatu kesatuan politik raya. Di antara kekaisaran-kekaisaran besar dalam sejarah kemanusiaan dapat ditemukan, misalnya, Kerajaan Spanyol pertama kemudian, Kerajaan Inggris , yang pada zaman...

طائرة عائمة دي هافيلاند توين أوتر تكمل هبوطها على الماء رحلة الخطوط الجوية الأمريكية رقم 1549 «حَطَّت على الماء» في نهر هدسون في عام 2009 وبقي جميع الركاب على قيد الحياة. في مجال الطيران، الهبوط على الماء (water landing)، يعتبر بالمعنى الواسع، هبوط طائرة على مسطح مائي. تهبط الطائرات ا...
















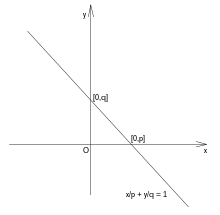


























![{\displaystyle A=[x_{0},y_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b3329e1cf12b53aaf1ac606c7414d885ea17139)










![{\displaystyle [x_{0},y_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d3caa55d3f5b0f9ed69a4352c251877397060fb)

![{\displaystyle [x_{1},y_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/803462d0ee7e478032128b2efc576d4dd7b821e3)
![{\displaystyle [x_{2},y_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32c6a746d50d795c9b47d483370a561d9b9ea276)




![{\displaystyle [x_{1},y_{1}],[x_{2},y_{2}],[x_{3},y_{3}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7a573c6737fe176ae1ae5571e8a32bdc173d6d0)













![{\displaystyle [x_{0},y_{0},z_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/783963bcced1f79ece185af36af724239002afaa)





![{\displaystyle [x_{1},y_{1},z_{1}],[x_{2},y_{2},z_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca6ecc8e08f8f8570262ecc1329562b3ef5f9b65)

![{\displaystyle [x_{1},y_{1},z_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0c388d9b95453e0fc82d4267fbdc0fd13cf5314)



















