Balmerova série
|
Read other articles:

Часть серии статей о Холокосте Идеология и политика Расовая гигиена · Расовый антисемитизм · Нацистская расовая политика · Нюрнбергские расовые законы Шоа Лагеря смерти Белжец · Дахау · Майданек · Малый Тростенец · Маутхаузен ·&...

Untuk Provinsi Chiang Mai, lihat Provinsi Chiang Mai. Koordinat: 18°47′18″N 98°59′07″E / 18.78833°N 98.98528°E / 18.78833; 98.98528 Chiang Mai (Thai: เชียงใหม่code: th is deprecated ), juga sering kali disebut Chiengmai, adalah kota terbesar ke-2 di Thailand dan terbesar di utara Thailand. Terletak di antara pegunungan yang membentuk daerah utara Thailand, Chiang Mai berjarak sekitar 700 kilometer sebelah barat laut Bangkok. Chiang Mai jug...

Province of South Korea This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: North Jeolla Province – news · newspapers · books · scholar · JSTOR (July 2021) (Learn how and when to remove this template message) Special Self-governing Province in Honam, South KoreaJeonbuk State 전북특별자치도Special Self-gov...

Edward Lee Thorndike, tokoh psikologi pendidikan yang mengembangkan teori koneksionisme. Koneksionisme atau teori coba-coba adalah sebuah teori belajar yang dikemukakan oleh Edward Lee Thorndike. Teori ini menyatakan bahwa perilaku setiap makhluk hidup merupakan hubungan antara rangsangan dan tanggapan.[1] Prinsip dari teori koneksionisme adalah asosiasi.[2] Pengembangan teori koneksionisme didasarkan kepada percobaan oleh Thorndike yang dilakukannya terhadap ayam dan kucing.&...

If U Seek AmySingel oleh Britney Spearsdari album CircusDirilis10 Maret 2009 (2009-03-10)Direkam2008Genre Dance-pop electropop Durasi3:36Label Jive Zomba Pencipta Max Martin Shellback Savan Kotecha Alexander Kronlund Produser Max Martin Kronologi singel Britney Spears Circus (2008) If U Seek Amy (2009) Radar (2009) Video musikIf U Seek Amy di YouTube If U Seek Amy adalah lagu oleh penyanyi asal Amerika Serikat, Britney Spears, dari album studio keenamnya, Circus (2008). Lagu ini dirilis ...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Universitas Sulawesi Barat – berita · surat kabar · buku · cendekiawan · JSTORUniversitas Sulawesi BaratJenisPerguruan Tinggi NegeriDidirikan31 November 2007Lembaga indukKementerian Pendidikan, Kebudayaa...

Structure in Montreal This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Nicolaus Copernicus Monument, Montreal – news · newspapers · books · scholar · JSTOR (March 2018) (Learn how and when to remove this template message) Nicolaus Copernicus MonumentFrench: Monument à Nicolas CopernicThe monument in 2017Loca...

Formule développée de l'ion oxalate. L'ion oxalate, aussi appelé éthanedioate C2O42−, est la dibase conjuguée d'un diacide, l'acide oxalique (ou acide éthanedioïque) H2C2O4, le plus simple des acides dicarboxyliques (HOOC–COOH). Les couples acide/base concernés sont : l'acide oxalique et sa base conjuguée l'ion hydrogénoxalate H2C2O4 / HC2O4− ; l'ion hydrogénoxalate et sa base conjuguée l'ion oxalate HC2O4− / C2O42−. Propriétés Demi-équations acide-base H2C2...

Pour les articles homonymes, voir Coletti. Alexandra Coletti Alexandra Coletti en 2011. Contexte général Sport Ski alpin Période active 1998-2019 Biographie Nationalité sportive Italie puis Monaco (depuis 2005) Nationalité Italie et Monaco Naissance 8 août 1983 (40 ans) Lieu de naissance La Colle-sur-Loup, France Taille 1,64 m (5′ 5″) Poids de forme 60 kg (132 lb) Club Monte Carlo ski club modifier Alexandra Coletti, née le 8 août 1983 à La Colle-s...

Part of a series onTaxation An aspect of fiscal policy Policies Government revenue Property tax equalization Tax revenue Non-tax revenue Tax law Tax bracket Flat tax Tax threshold Exemption Credit Deduction Tax shift Tax cut Tax holiday Tax amnesty Tax advantage Tax incentive Tax reform Tax harmonization Tax competition Tax withholding Double taxation Representation Unions Medical savings account Economics General Theory Price effect Excess burden Tax incidence Laffer curve Optimal tax Theori...

1992 film De NoorderlingenDirected byAlex van WarmerdamWritten byAlex van WarmerdamProduced byLaurens GeelsDick MaasStarringJack WouterseAnnet MalherbeRudolf LucieerEdited byRené WiegmansMusic byVincent van WarmerdamDistributed byFirst Floor FeaturesRelease date 17 April 1992 (1992-04-17) Running time108 minutesCountryNetherlandsLanguageDutch The Northerners (Dutch: De Noorderlingen) is a 1992 Dutch film by Alex van Warmerdam. The film was selected as the Dutch entry for the B...

1911 book by Jack London First edition (publ. Macmillan) The Cruise of the Snark (1911)[1] is a non-fictional, illustrated book by Jack London chronicling his sailing adventure in 1907 across the south Pacific in his ketch the Snark. Accompanying London on this voyage was his wife Charmian London and a small crew. London taught himself celestial navigation and the basics of sailing and of boats during the course of this adventure and describes these details to the reader. He visits ex...

ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Раннее христианство Гностическое христианство Вселенские соборы Н...

Interdisciplinary study and analysis of health politics Elizabeth Warren and Bernie Sanders campaigning for extended US Medicare coverage in 2017. Part of a series onPublic health Outline Subfields Community health Dental public health Environmental health Epidemiology Health economics Health education Health promotion Health policy Health politics Mental health Occupational safety Rehabilitation (penology) Sexual and reproductive health Sanitation World health (Global health - International ...
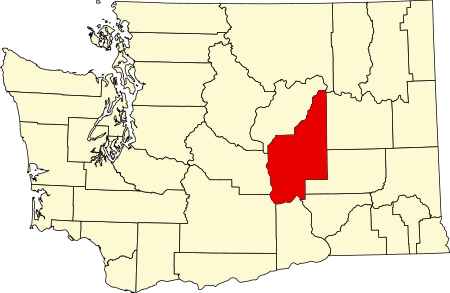
Эта статья об округе в штате Вашингтон; другие значения: Грант (округ). ОкругГрантангл. Grant County 47°13′ с. ш. 119°28′ з. д.HGЯO Страна США Входит в штат Вашингтон Адм. центр Эфрейта[англ.] История и география Дата образования 24 февраля 1909 Площадь 7229 км² (6944 км² — с�...

Tari Topeng kelana yang dipentaskan di Area Wisata Batik Trusmi Cirebon Tari Topeng Cirebon (Bahasa Cirebon: beksan topeng Cerbon) adalah salah satu tarian di wilayah kesultanan Cirebon. Pada awalnya tari topeng bermula sejak era Jawa Kuno di Jawa Timur. Pada masa-masa selanjutnya berkembang dan menyebar ke Jawa Tengah, Cirebon, bahkan juga Banjar dan Kutai. Tari Topeng Cirebon, berkembang di daerah Cirebon, termasuk Subang, Indramayu, Jatibarang, Majalengka, Losari, dan Brebes. Disebut tari ...

Louis Marcoussis: Selbstporträt, 1936, Radierung, Cleveland Museum of Art Louis Marcoussis, dulunya disebut Ludwik Kazimierz Wladyslaw Markus atau Ludwig Casimir Ladislas Markus, (1878 atau 1883,[1] Łódź – 22 Oktober 1941, Cusset) adalah seorang pelukis dan engraver keturunan Polandia. Ia tinggal di Paris selama sebagian masa hidupnya dan menjadi warga negara Prancis. Referensi ^ November 10, 1878 is the date preferred by the Grove Dictionary of Art among others, but some reputa...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

2004 Indian filmGudumba ShankarDirected byVeera ShankarScreenplay byPawan Kalyan Dialogues bySatyanand Story bySatyanandProduced byNagendra BabuStarringPawan KalyanMeera JasmineAshish VidyarthiCinematographyChota K. NaiduEdited byYusuf KhanMusic byMani SharmaProductioncompanyAnjana ProductionsRelease date 10 September 2004 (2004-09-10) Running time176 minutesCountryIndiaLanguageTelugu Gudumba Shankar is a 2004 Indian Telugu-language action comedy film directed by Veera Shankar...

German politician Kurt SchmückerSchmücker in 1971Federal Minister for the TreasuryIn office1 December 1966 – 21 October 1969Preceded byWerner DollingerFederal Minister of FinanceIn office8 November 1966 – 2 December 1966Preceded byRolf DahlgrünSucceeded byFranz Josef StraussFederal Minister of EconomicsIn office17 October 1963 – 30 November 1966[1]Preceded byLudwig ErhardSucceeded byKarl SchillerMember of the BundestagIn office7 September 1949 ...



