Algebraický výraz
|
Read other articles:

GairPosterSutradaraAshok GaikwadProduserHarish Sapkale,Prakash PatilDitulis olehSantosh Saroj (dialogues)CeritaRajeev Kaul,Praful ParekhPemeranAjay DevgnRaveena TandonReena RoyAmrish PuriParesh RawalPenata musikAnand MilindSinematograferAnwar SirajPenyuntingWaman Bhonsle,Gurudutt ShiraliTanggal rilis 12 November 1999 (1999-11-12) Durasi145 minutesNegaraIndiaBahasaHindiAnggaran3.50cr[1]Pendapatankotor5.81cr[1]Gair adalah sebuah film drama kejahatan aksi berbahasa Hin...

Logam yang dipanaskan akan membuat atom-atom pada logam bergetar semakin cepat. Akibatnya atom-atom tersebut menghasilkan gelombang elektromagnetik (cahaya) Proses pemanasan berkelanjutan dapat ditemukan pada matahari dan bumi. Beberapa radiasi termal matahari menyerang dan memanaskan bumi. Dibandingkan dengan matahari, bumi memiliki suhu yang jauh lebih rendah sehingga mengirimkan radiasi termal yang jauh lebih sedikit ke matahari. Panas dari proses ini dapat diukur dengan jumlah bersih, dan...

National association football team This article is about the men's team. For the women's team, see Macau women's national football team. MacauNickname(s)Selecção do Lótus (The Lotus' Team)Verdes (The Greens)AssociationAssociação de Futebol de MacauConfederationAFC (Asia)Sub-confederationEAFF (East Asia)Head coachLázaro OliveiraCaptainNiki TorrãoMost capsCheang Cheng Ieong (58)Top scorerChan Kin Seng (17)[1]Home stadiumEstádio Campo DesportivoFIFA codeMAC First colours Second c...

Sultanate of Muscat and Oman (red), shown with the Imamate of Oman (orange) and the Trucial States (grey). This is a list of British representatives in Muscat and Oman from 1800 to 1971. They were responsible for representing British interests in the Sultanate of Muscat and Oman while the country was a British protectorate (from 20 March 1891 until 2 December 1971). Muscat and Oman was reconstituted as the modern-day Sultanate of Oman after the protectorate ended. For British representatives...

Part of a series onBritish law Acts of Parliament of the United Kingdom Year 1801 1802 1803 1804 1805 1806 1807 1808 1809 1810 1811 1812 1813 1814 1815 1816 1817 1818 1819 1820 1821 1822 1823 1824 1825 1826 1827 1828 1829 1830 1831 1832 1833 1834 1835 1836 1837 1838 1839 1840 1841 1842 1843 1844 1845 1846 1847 1848 1849 1850 1851 1852 1853 1854 1855 1856 1857 1858 1859 1860 1861 1862 1863 1864 1865 1866 1867 1868 1869 1870 1871 1872 1873 1874 1875 1876 1877 1878 ...

2005 Doctor Who episode163 – Father's DayDoctor Who episodeCastDoctor Christopher Eccleston – Ninth Doctor Companion Billie Piper – Rose Tyler Others Camille Coduri – Jackie Tyler Shaun Dingwall – Pete Tyler Robert Barton – Registrar Julia Joyce – Young Rose Christopher Llewellyn – Stuart Frank Rozelaar-Green – Sonny Natalie Jones – Sarah Eirlys Bellin – Bev Rhian James – Suzie Casey Dyer – Young Mickey ProductionDirected byJoe AhearneWritten byPaul CornellS...

Shalom SimhonLahir7 Desember 1956 (umur 67)Tempat lahirKfar Saba, IsraelKnesset14, 15, 16, 17, 18Faksi yang diwakili di Knesset1996–1999Partai Buruh1999–2001One Israel2001–2011Partai Buruh2011–2013IndependenceJabatan menteri2001–2002Menteri Pertanian2005Menteri Lingkungan Hidup2006–2011Menteri Pertanian2011–2013Menteri Industri, Perdagangan & Buruh2011–2013Menteri Minoritas Shalom Simhon (Ibrani: שלום שמחון, lahir 7 Desember 1956) adalah seorang politikus...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

African television channel This article is about the 24 hour Music channel in Africa. For the Music channel in the UK and Ireland, see MTV Base. For the defunct Music Channel in France, see MTV Base (French TV channel). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: MTV Base African TV channel – news · newspapers �...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Halaman ini berisi artikel tentang peramban web. Untuk sistem operasi, lihat ChromeOS.Google Chrome Google Chrome berjalan di Windows 11Tipeperamban web, aplikasi dan Perangkat lunak milik perorangan BerdasarkaChromium Versi pertama2 September 2008; 15 tahun lalu (2008-09-02)Versi stabilDaftarMicrosoft Windows, macOS, Linux: 124.0.6367.155/156 (7 Mei 2024)Microsoft Windows, macOS: 124.0.6367.155 (7 Mei 2024)Android: 124.0.6367.159 (7 Mei 2024)iOS: 125.0.6422.33 (8 Mei 2024) Versi sebelum...

Численность населения республики по данным Росстата составляет 4 003 016[1] чел. (2024). Татарстан занимает 8-е место по численности населения среди субъектов Российской Федерации[2]. Плотность населения — 59,00 чел./км² (2024). Городское население — 76,72[3] % (20...
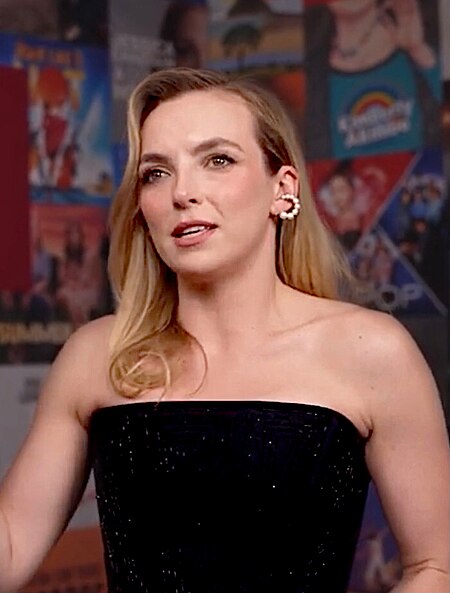
Jodie Comer (2023) Jodie Marie Comer (Liverpool, 11 marzo 1993) è un'attrice britannica. È nota per il ruolo di Villanelle nella serie televisiva Killing Eve (2018-22), per la quale si aggiudica il BAFTA Television Award e il Premio Emmy nella sezione miglior attrice in una serie drammatica, venendo inoltre nominata due volte al Golden Globe, due al Critics Choice Television Award e una allo Screen Actors Guild Award. Nel 2022 ha vinto il Critics Choice Super Award perThe Last Duel di Ridle...

Music school in Germany Frankfurt University of Music and Performing ArtsHochschule für Musik und Darstellende Kunst Frankfurt am MainTypeStateEstablished1938; 86 years ago (1938)ChancellorAngelika GartnerPresidentElmar Fulda[1]Vice-president Maria Spychiger Hubert Buchberger Academic staff385Students900LocationFrankfurt, Hesse, Germany50°07′12″N 8°40′34″E / 50.1201°N 8.6762°E / 50.1201; 8.6762Websitehfmdk-frankfurt.de The Frankfu...

Cet article est une ébauche concernant une localité allemande. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Simbach am Inn L'hôtel de ville de Simbach am Inn. Armoiries Administration Pays Allemagne Land Bavière District(Regierungsbezirk) Basse-Bavière Arrondissement(Landkreis) Rottal-Inn Bourgmestre(Bürgermeister) Günther Wöhl Code postal 84359 Code communal(Gemeindeschlüssel) 09 2 77 145 Indicatif ...

Ciclismo en los Juegos Olímpicos de 2016 Recorrido de la prueba de ciclismo en contrarreloj masculinoDatos generalesSede Río de JaneiroBrasil BrasilCategoría Carrera contrarreloj masculinaFecha 10 de agosto de 2016Organizador Comité Olímpico InternacionalCircuitoDistancia total 54,56Palmarés01 ! Oro Fabian Cancellara02 ! Plata Tom Dumoulin03 ! Bronce Christopher FroomeDatos estadísticosParticipantes 37 de 29 países Cronología 2012 2016 2020 Sitio oficial [edita...
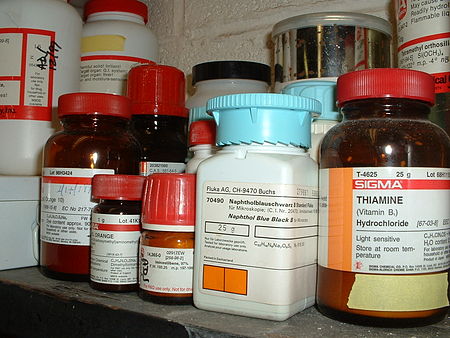
Questa voce o sezione sull'argomento composti chimici non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Flaconi contenenti vari composti chimici in un laboratorio chimico Un composto chimico, in chimica, indica ogni sostanza pura che può essere decomposta con gli ordinari mezzi chimici in altre sostanze pure più semplici.[1] Generalmente si parla...

Digital audio workstation Not to be confused with Dolby Pro Logic. Logic ProA screenshot of Logic Pro X running on macOS MojaveDeveloper(s)Apple Inc.Initial release1993; 31 years ago (1993) (as Notator Logic)Stable release11.0 / May 13, 2024; 40 days ago (2024-05-13) Written inC (programming language)Operating systemmacOS (13.5 and later) iPadOS (17.0 or newer)Platformx86-64 (as of Logic Pro 9.1)[1] ARM64 (as of Logic Pro 10.6)TypeMIDI sequencer and...

Greek Orthodox monastery in Constantinople Studite monks redirects here. For the Ukrainian religious society, see Studite Brethren. Byzantine miniature depicting the Stoudios Monastery and the Propontis (Sea of Marmara), from the Menologion of Basil II (c. 1000). The Monastery of Stoudios, more fully Monastery of Saint John the Forerunner at Stoudios (Greek: Μονή του Αγίου Ιωάννη του Προδρόμου εν τοις Στουδίου, translit. Monē tou Hagiou Iōann...

Series of televised debates sponsored by CNN and YouTube This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: CNN/YouTube presidential debates – news · newspapers · books&#...







![{\displaystyle a^{\frac {m}{n}}={\sqrt[{n}]{a^{m}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb409de8f30f86d2ee48c97de1f939fdd257d916)










![{\displaystyle 2{\sqrt[{}]{2}}+y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4134d089223c8478b2a8ef7c17f83bba4f46532c)



















