Teorema d'Euclides
| ||||||||
Read other articles:

Bat Yam בַּת יָםDistrikTemplat:Country data Distrik Tel AvivDidirikan1926Pemerintahan • JenisKota (sejak 1958) • Kepala DaerahShlomo LahianiLuas • Total8.167 dunams (8,167 km2 or 3,153 sq mi)Populasi (2007) • Total129.100 • Kepadatan16/km2 (41/sq mi)Arti namalit. 'Daughter of the sea', can also mean 'mermaid' Pantai Bat Yam. The Defenters Square Bat Yam (Ibrani: בַּת יָם (audio)�...

Adriani ElisabethLisa tahun 2019Lahir10 Mei 2000 (umur 23)Purbalingga, Jawa Tengah, IndonesiaPekerjaanIdolDikenal atasPeringkat 4 (Senbatsu) — JKT48 Janken Competition 2016Karier musikGenrePopJ-PopInstrumenVokalTahun aktif2015 - 2021LabelHits RecordsDentsuX EntertainmentArtis terkaitJKT48Situs webJKT48AnggotaJKT48 (2015 - 2021) Adriani Elisabeth (lahir 10 Mei 2000) yang sebelumnya di kenal sebagai Lisa JKT48 adalah seorang penyanyi dan penari yang bergabung dalam idol grup JKT48 asal ...

Need for Speed: Most Wanted Sampul Need for Speed: Most Wanted versi Xbox 360PublikasiPS2, XB, GC: AS: 15 November 2005PAL: 24 November 2005 Xbox 360: AS: 22 November 2005PAL: 2 Desember 2005 Telepon genggam: AS: 21 Desember 2005 PC dan PSP AS: 21 Desember 2005GenreBalapanLatar tempatNeed for Speed universe (en) Bahasa Daftar Inggris 60 Karakteristik teknisPlatformNintendo DS, Game Boy Advance, Xbox 360, Xbox, PlayStation 2, Windows, PlayStation Portable, PlayStation 3, Nintendo GameCube dan ...

You can help expand this article with text translated from the corresponding article in Polish. Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Do not translate text that appears unreliable or low-quality. If possibl...
French actor (1925–2006) This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (January 2013) (Learn how and when to remove this template message) Darry CowlCowl at 2001 César ceremonyBornAndré Darricau(1925-08-27)27 August 1925Vittel, FranceDied14 February 2006(2006-02-14) (aged 80)Neuilly-sur-Seine, FranceNationalityFren...

Bernard Sumner Tidigare namnBernard Albrecht, Bernard Dicken, BarneyFödelsedatum4 januari 1956 (68 år)FödelseortBroughton, Salford, Greater Manchester, EnglandGenrerRock, postpunk, new wave, syntpop, electronicaRollMusiker, låtskrivare, musikproducent, remixerInstrumentSång, gitarr, keyboard, synthesizer, melodikaÅr som aktiv1973 –SkivbolagFactory Records, London Records, Warner Bros. Records, Parlophone, Mute Records, Triple EchoRelaterade artisterJoy Division, New Order, E...

Европейская сардина Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеГруппа:Костные рыбыКласс:Лучепёрые рыбыПодкласс:Новопёры...

SebuyauNegara MalaysiaNegara Bagian Sarawak Sebuyau adalah sebuah kota di pesisir Sarawak. Berbatasan dengan Sri Aman dan Simunjan di pulau Kalimantan. Sebagian besar penduduknya terdiri dari Melayu dan orang-orang Iban. Pranala luar Sebuyau.Net Community Portal Diarsipkan 2022-01-22 di Wayback Machine. lbs Sarawak Bumi KenyalangKumpulan etnis Bisaya Melayu Brunei Kedayan Melayu Sarawak Dayak Bidayuh Bukitan Iban Selako Orang Ulu Kayan Kelabit Kenyah Lun Bawang Penan Punan Ukit Mela...

Scott Act (1888)Long titleAn Act a supplement to an act entitled An Act to execute certain treaty stipulations relating to Chinese, approved the sixth day of May eighteen hundred and eighty-two.NicknamesChinese Exclusion Law of 1888Enacted bythe 50th United States CongressEffectiveOctober 1, 1888CitationsPublic law50-1064Statutes at Large25 Stat. 504Legislative historyIntroduced in the House as H.R. 11336 by William Lawrence Scott (D–PA) on July 15, 1888Passed the Senate...

Municipal unit in Dibër, AlbaniaMaqellarëMunicipal unitMaqellarëCoordinates: 41°35′N 20°30′E / 41.583°N 20.500°E / 41.583; 20.500Country AlbaniaCountyDibërMunicipalityDibërPopulation (2011) • Municipal unit10,662Time zoneUTC+1 (CET) • Summer (DST)UTC+2 (CEST) Maqellarë (Macedonian: Макелари/Makelari or Макеларе/Makelare) is a village and a former municipality in the Dibër County, northeastern Albania. At ...

The Gradiva, an example of a Neo-Attic sculpture Another Neo-Attic relief (British Museum) Neo-Attic or Atticizing is a sculptural style, beginning in Hellenistic sculpture and vase-painting of the 2nd century BC and climaxing in Roman art of the 2nd century AD, copying, adapting or closely following the style shown in reliefs and statues of the Classical (5th–4th centuries BC) and Archaic (6th century BC) periods.[1] It was first produced by a number of Neo-Attic workshops at Athen...

Bài này viết về một hiện tượng vật lý. Đối với các định nghĩa khác, xem Điện (định hướng). Tia sét và chiếu sáng đô thị là hai trong những hiện tượng ấn tượng nhất của điện. Bài viết vềĐiện từ học Điện Từ học Lịch sử Giáo trình Tĩnh điện Chất cách điện Chất dẫn điện Cảm ứng tĩnh điện Điện ma sát Điện thông Điện thế Điện trường Điện tích Định luật Coulo...

Champlain in Concarneau before her launch, in September 2016 Class overview NameBâtiment multi-mission BuildersKership (DCNS-Piriou joint venture), Concarneau Operators Marine Nationale Preceded byBATRAL-class landing ship Planned4 Active4 General characteristics TypeOffshore patrol vessel[2][3] Displacement 1,500 tonnes (empty) 2,300 tonnes (full load)[1] Length65 m (213 ft 3 in)[1] Beam14 m (45 ft 11 in)[1 ...
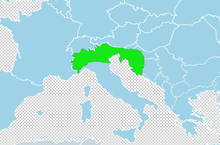
Species of fish Salmo marmoratus Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Actinopterygii Order: Salmoniformes Family: Salmonidae Genus: Salmo Species: S. marmoratus Binomial name Salmo marmoratusG. Cuvier, 1829 Salmo marmoratus, the marble trout, is a species of freshwater fish in the family Salmonidae. It is characterized by a distinctive marbled color pattern and high growth capac...

لمعانٍ أخرى، طالع وزارة الخارجية (توضيح). جمهورية السودانوزارة الخارجية وزارة الخارجية (السودان) تفاصيل الوكالة الحكومية البلد السودان الاسم الكامل وزارة الخارجية تأسست يناير 1956 المركز الخرطوم، السودان الإدارة منصب المدير وزير الخارجية [لغات أخرى]&...

Order of mammals For information on all meat-eating organisms, see Carnivores. For the alternative medicine Carnivorans, see Venus flytrap § In alternative medicine. CarnivoransTemporal range: 51.88–0 Ma PreꞒ Ꞓ O S D C P T J K Pg N Early Eocene-Holocene[1] Various carnivorans, with feliforms to the left, and caniforms to the right Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Clade: Carnivoramorpha Clade: Carnivoraforme...

Governor of São PauloStandard of the governorIncumbentTarcísio de Freitassince 1 January 2023StyleMr. Governor or even simply Governor(informal)Most Excellent Mr. Governor(formal)His Excellency(alternative formal, diplomatic)StatusHead of stateHead of governmentResidencePalácio dos BandeirantesAppointerPopular voteTerm lengthFour years,renewable once consecutivelyConstituting instrument1989 State ConstitutionPrecursorPresident of São Paulo ProvinceInaugural holderPrudente de MoraesF...

Genus of amphibians For the Saint Caecilia, see Cecilia (saint). For the Ancient Roman family, see Caecilia gens. Caecilia Caecilia nigricans Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Amphibia Order: Gymnophiona Clade: Apoda Family: Caeciliidae Genus: CaeciliaLinnaeus, 1758 Type species Caecilia tentaculataLinnaeus, 1758 Diversity See text Caecilia is a genus of amphibians in the family Caeciliidae. Species Binomial name and author Common name Caeci...

639–646 Rashidun Caliphate campaign Arab conquest of EgyptPart of the Arab–Byzantine warsRoman Theater in the city of Alexandria, EgyptDate639–642LocationEgypt, LibyaResult Rashidun victoryTerritorialchanges Rashidun Caliphate annexes Egypt, Cyrenaica, and TripolitaniaBelligerents Rashidun Caliphate Byzantine Empire Kingdom of Makuria Commanders and leaders Umar ibn al-Khattab Amr ibn al-As Uqba ibn Nafi Zubayr ibn al-Awwam Miqdad ibn Aswad Ubadah ibn al-Samit Kharija ibn Hudhafa Busr i...

Spanish general and political figure (1629–1679) For other people named John of Austria, see John of Austria (disambiguation). You can help expand this article with text translated from the corresponding article in Spanish. (October 2012) Click [show] for important translation instructions. View a machine-translated version of the Spanish article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as nece...








