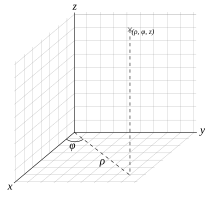
Sistema de coordenades esfèriques
|
Read other articles:

Artur AvilaLahir29 Juni 1979 (umur 44)Rio de Janeiro, BrasilTempat tinggalRio de Janeiro, Brasil dan Paris, PrancisWarga negaraBrasil dan Prancis[1]AlmamaterUniversitas Federal Rio de JaneiroInstituto Nacional de Matemática Pura e AplicadaDikenal atasSistem dinamikaTeori spektrumPenghargaanFields Medal (2014)IAMP Early Career Award (2012)Michael Brin Prize (2011)Herbrand Prize (2009)EMS Prize (2008)Salem Prize (2006)Karier ilmiahBidangMatematikaInstitusiCNRS, IMJ-PRGUniversitas...

Untuk orang lain dengan nama yang sama, lihat Iwan Kurniawan. Iwan Kurniawan Anggota Dewan Perwakilan RakyatPetahanaMulai menjabat 1 Oktober 2014Daerah pemilihanKalimantan Tengah Informasi pribadiLahir(1970-05-12)12 Mei 1970Banjarmasin, Kalimantan Selatan, IndonesiaPartai politikGerindraAlma materUniversitas Tri Tunggal SurabayaPekerjaanPolitikusSunting kotak info • L • B H. Iwan Kurniawan, S.H. (lahir 12 Mei 1970) adalah seorang politikus Indonesia. Saat ini ia menjabat seb...

A numerical solution to the one dimensional Allen-Cahn equation The Allen–Cahn equation (after John W. Cahn and Sam Allen) is a reaction–diffusion equation of mathematical physics which describes the process of phase separation in multi-component alloy systems, including order-disorder transitions. The equation describes the time evolution of a scalar-valued state variable η {\displaystyle \eta } on a domain Ω {\displaystyle \Omega } during a time interval T {\displaystyle {...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

此條目可参照英語維基百科相應條目来扩充。 (2017年8月)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 密西西比州 美國联邦州State of Mississippi 州旗州徽綽號:木蘭之州地图中高亮部分为密西西比州坐标:30°13'N�...

第三十二届夏季奥林匹克运动会柔道比賽比賽場館日本武道館日期2021年7月24日至31日項目數15参赛选手393(含未上场5人)位選手,來自128(含未上场4队)個國家和地區← 20162024 → 2020年夏季奥林匹克运动会柔道比赛个人男子女子60公斤级48公斤级66公斤级52公斤级73公斤级57公斤级81公斤级63公斤级90公斤级70公斤级100公斤级78公斤级100公斤以上级78公斤以上级团体混...

Graeme Brown Graeme Brown nel 2010 Nazionalità Australia Altezza 178 cm Peso 75 kg Ciclismo Specialità Strada, pista CarrieraSquadre di club 2002-2005 Panaria2006-2012 Rabobank2013-2014 Blanco2015-2016 DrapacPalmarès Giochi olimpici Oro Atene 2004 Americana Oro Atene 2004 Ins. squadre Mondiali su pista Oro Città del Capo 1997 Ins. sq. J Oro Stoccarda 2003 Ins. squadre Argento Manchester 2008 Ins. squadre Statistiche aggiornate al aprile 2016 Modi...

Human settlement in EnglandSt LevanCornish: SelevanParish church of St LevanSt LevanLocation within CornwallPopulation459 (2011)OS grid referenceSW3822Civil parishSt LevanUnitary authorityCornwallCeremonial countyCornwallRegionSouth WestCountryEnglandSovereign stateUnited KingdomPost townPENZANCEPostcode districtTR19Dialling code01736PoliceDevon and CornwallFireCornwallAmbulanceSouth Western UK ParliamentSt Ives List of places UK England Cornwall ...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Indoor sporting arena and multi-purpose venue in Barcelona, Spain Palau Sant JordiPalau Sant Jordi in June 2013LocationPasseig Olímpic, 5-7, 08038 BarcelonaCoordinates41°21′48.2″N 2°09′09.2″E / 41.363389°N 2.152556°E / 41.363389; 2.152556OwnerBarcelona City CouncilOperatorBarcelona de Serveis Municipals (B:SM)Capacity17,960 (Main Hall)3,000 (Sant Jordi Club)SurfaceParquetConstructionBroke ground1986Built1986–90Opened21 September 1990Renovated2014Expanded...

Райли Макгри Общая информация Полное имя Райли Патрик Макгри Родился 2 ноября 1998(1998-11-02)[1][2] (25 лет)Аделаида, Австралия Гражданство Австралия Рост 178 см Позиция атакующий полузащитник Информация о клубе Клуб Мидлсбро Номер 8 Молодёжные клубы 2014—2016 Аделаида Юна...

Cyperus gilesii Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Tracheophyta (tanpa takson): Angiospermae (tanpa takson): Monokotil (tanpa takson): Komelinid Ordo: Poales Famili: Cyperaceae Genus: Cyperus Spesies: Cyperus gilesii Nama binomial Cyperus gilesiiBenth. Bunga Cyperus gilesii Buah Cyperus gilesii Cyperus gilesii adalah spesies tumbuhan yang tergolong ke dalam famili Cyperaceae. Spesies ini juga merupakan bagian dari ordo Poales. Spesies Cyperus gilesii sendiri merupakan bagia...

Questa voce sull'argomento centri abitati del Paraná è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Ângulocomune LocalizzazioneStato Brasile Stato federato Paraná MesoregioneNorte Central Paranaense MicroregioneAstorga AmministrazioneSindacoPedro Vicentin (Cidadania) dal 2013 Data di istituzione1990 TerritorioCoordinate23°11′45″S 51°54′34″W23°11′45″S, 51°54′34″W (Ângulo) Altitudine300 m s.l.m....

Pakatan Rakyat Ketua umumAnwar Ibrahim Lim Kit Siang Abdul Hadi AwangDibentuk1 April 2008Dibubarkan16 Juli 2015Didahului olehBarisan AlternatifDiteruskan olehPakatan HarapanKantor pusatPetaling Jaya, Malaysia (DAP & PKR) Kuala Lumpur, Malaysia (PAS)Keanggotaan Partai Keadilan Rakyat (PKR) Partai Aksi Demokratis (DAP) Partai Islam Se-Malaysia (PAS)IdeologiHybridDewan Rakyat:89 / 222 Dewan Undangan Negeri:241 / 576 Politik MalaysiaPartai politikPemilihan umum Pakatan Rakyat atau P...

Jean Zimmer Informasi pribadiTanggal lahir 6 Desember 1993 (umur 30)Tempat lahir Bad Dürkheim, JermanTinggi 171 m (561 ft)Posisi bermain Bek kananInformasi klubKlub saat ini VfB StuttgartNomor 6Karier junior-2013 1. FC KaiserslauternKarier senior*Tahun Tim Tampil (Gol)2012–2014 1. FC Kaiserslautern II 59 (1)2013–2016 1. FC Kaiserslautern 61 (5)2016– VfB Stuttgart Tim nasional‡2014– Jerman U21 1 (0) * Penampilan dan gol di klub senior hanya dihitung dari liga domesti...

1800 battle during the War of the Second Coalition This article is about the battle in 1800. For the battle in 1796, see Battle of Biberach (1796). Battle of Biberach (1800)Part of the French Revolutionary WarsPainting by Johann Baptist Pflug shows an Austrian commander leading his soldiers against the French.Date9 May 1800LocationBiberach an der Riss, present-day Germany48°06″N 9°48″E / 48.00167°N 9.01333°E / 48.00167; 9.01333Result French victoryBelligerents ...

François-André Danican PhilidorPortrait gravé (1772) par Augustin de Saint-Aubin d'après Charles-Nicolas Cochin.BiographieNaissance 7 septembre 1726DreuxDécès 31 août 1795 (à 68 ans)LondresNationalité françaiseActivités Acteur, compositeur, musicien, pianiste, joueur d'échecs, théoricien du jeu d'échecsFamille Famille PhilidorPère André Danican PhilidorFratrie Anne Danican PhilidorAutres informationsMouvement Musique classiqueSport ÉchecsInstrument PianoGenre artistique ...

Cet article est une ébauche concernant le Danemark. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Forces armées danoisesForsvaret Armoiries des forces armées danoises Branches Armée royale danoise (en)Marine royale danoiseArmée de l'air royale danoiseGarde nationale danoise (en) Commandement Roi du Danemark Frédéric X de Danemark Ministre de la Défense Peter Christensen Venstre Chef d'état-m...

Measure for evaluating probabilistic forecasts Not to be confused with Score voting. It has been suggested that this article be merged with Loss functions for classification. (Discuss) Proposed since April 2024. Visualization of the expected score under various predictions from some common scoring functions. Dashed black line: forecaster's true belief, red: linear, orange: spherical, purple: quadratic, green: log. In decision theory, a scoring rule[1] provides evaluation metrics for p...

Cámara de Representantes de Prusia en 1900. Cámara de los Señores de Prusia en 1900. El sufragio prusiano de tres clases (en alemán: Preußisches Dreiklassenwahlrecht), conocido coloquialmente como sistema de las tres clases, fue un sistema electoral indirecto utilizado desde 1848 hasta 1918 en el Reino de Prusia y durante períodos más breves en otros estados alemanes. Los votantes se agrupaban por distrito en tres clases, con los pagos totales de impuestos en cada clase iguales. Los qu...