Problema dels dos cossos
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2023. DinamikAsal Pahang, MalaysiaGenreRock & BaladaPekerjaanVokal / PemusikTahun aktif1990-1992Situs webKumpulan DinamikAnggotaNai - Vokal Norin - 1st Lead Jeff - 2nd Lead Nan - Bass Lie - DramMantan anggotaMozri - Vokal Fauzi - Dram Leman - Dram Dinamik ...

Scott CaanScott Caan, Mei 2007LahirScott Andrew Caan23 Agustus 1976 (umur 47)Los Angeles, Kalifornia, Amerika SerikatPekerjaanAktorTahun aktif1995–sekarang Scott Andrew Caan (lahir 23 Agustus 1976) adalah aktor asal Amerika Serikat. Ia adalah bintang serial televisi CBS Hawaii Five-0, yang dinominasikan untuk penghargaan Golden . Ia adalah putra dari aktor James Caan. Filmografi Caan di 2006 Toronto International Film Festival Tahun Judul Peran 1995 A Boy Called Hate Hate 1997 No...
Untuk penggunaan di Wikipedia bahasa Indonesia, Lihat Wikipedia:VisualEditor. VisualEditor TipeMediaWiki extension (en), Penyunting teks dan halaman duplikat permanen Wikimedia GenreWikiLisensilisensi MIT[1]Karakteristik teknisBahasa pemrogramanPHP Informasi pengembangPengembangWikimedia Foundation dan WikiaInformasi tambahanSitus webVisualEditor Sunting di Wikidata • L • B • Bantuan penggunaan templat ini VisualEditor (VE) adalah sebuah proyek MediaWiki untuk men...

2010 video game 2010 video gameThe 3rd BirthdayNorth American cover artDeveloper(s)HexaDrivePublisher(s)Square EnixDirector(s)Hajime TabataProducer(s)Yoshinori KitaseProgrammer(s)Kogi SugimotoArtist(s)Isamu KamikokuryoWriter(s)Toshimitsu TakeuchiMotomu ToriyamaComposer(s)Mitsuto SuzukiTsuyoshi SekitoYoko ShimomuraSeriesParasite EvePlatform(s)PlayStation PortableReleaseJP: December 22, 2010NA: March 29, 2011EU: April 1, 2011Genre(s)Third-person shooter, role-playing shooterMode(s)Single-player...

Koridor 5 Trans Metro PasundanDipatiukur—Jatinangor5DSalah satu armada Koridor 5 Trans Metro Pasundan di Halte UNPAD DipatiukurInformasi umumJenis layananBus Rapid TransitDaerah operasi Kota Bandung Kabupaten Bandung Kabupaten Sumedang Mulai beroperasi27 Desember 2021Operator saat iniDAMRILintas pelayananStasiun awalUNPAD DipatiukurStasiun akhirUNPAD JatinangorJarak tempuh 32,4 kilometer (Dipatiukur—Jatinangor) 38 kilometer (Jatinangor—Dipatiukur) Frekuensi perjalananSetiap hari pulang ...

The Reverend FatherJoaquín Sáenz y ArriagaPadre Joaquin se preparando para celebrar a missaArchdioceseArquidiocese de GuadalajaraOrdersOrdination30 de Abril de 1930by Por Francisco Orozco e Jiménez, templo de São Felipe de jesus. Cidade do MéxicoPersonal detailsBorn12 October 1899 MoréliaMexicoDied28 April 1976 (aged 76) cidade doMexicoBuriedPanteón Francés de la PiedadNationalityMexicanoParentsRafael Sáenz y Arriaga, Madalena burga de SáenzProfessionTheologianEducationTheology...

جمهورية كوريا 대한민국 (كورية) كوريا الجنوبيةعلم كوريا الجنوبية كوريا الجنوبيةشعار كوريا الجنوبية الشعار الوطني홍익인간; 弘益人間 (غير رسمي)(ترجمة: أفد على نطاق واسع عالم الإنسان) النشيد: نشيد كوريا الجنوبية الوطني الأرض والسكان إحداثيات 36°N 128°E / 36°N 128°E / ...

American politician (born 1967) For other politicians with similar names, see Michael Collins (disambiguation). Mike CollinsMember of the U.S. House of Representativesfrom Georgia's 10th districtIncumbentAssumed office January 3, 2023Preceded byJody Hice Personal detailsBorn (1967-07-02) July 2, 1967 (age 56)Jackson, Georgia, U.S.Political partyRepublicanSpouseLeigh Ann CollinsChildren3RelativesMac Collins (father)EducationGeorgia State University (BA)WebsiteHouse website...

Johannes Nikolaus Tetens Johannes Nikolaus Tetens (Tetenbüll, 16 settembre 1736 – Copenaghen, 17 agosto 1807) è stato un filosofo e matematico tedesco. Indice 1 Biografia 2 Traduzioni 3 Studi 4 Note 5 Bibliografia 6 Altri progetti 7 Collegamenti esterni Biografia Einleitung zur Berechnung der Leibrenten, 1785 (Milano, Fondazione Mansutti). Illustrazione relativa all'articolo Methodus inveniendi curvas... pubblicato sugli Acta Eruditorum del 1763 Fu chiamato lo Hume tedesco, sulla base del...

Lutung Budeng Status konservasi Rentan Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Mammalia Ordo: Primates Famili: Cercopithecidae Genus: Trachypithecus Spesies: T. auratus Nama binomial Trachypithecus auratus(É. Geoffroy, 1812) Sinonim Simia Maura Schreber, 1774: 107-108 (nom. suppress.) Cercopithecus auratus É. Geoffroy, 1812[1] (basionym) Semnopithecus Pyrrhus Horsfield, 1823. Presbytes cristata — Gray, 1843: 3. Pithecus pyrrhus sondaicus Robinson & K...

Head of the Council of Ministers of Cuba Prime Minister of CubaPrimer Ministro de CubaFlag of the prime minister of CubaIncumbentManuel Marrero Cruzsince 21 December 2019Council of Ministers of CubaGovernment of CubaStyleMr Premier (informal)TypeHead of governmentMember ofCouncil of MinistersCouncil of StateSeatHavanaNominatorPresident of CubaAppointerNational Assembly of People's PowerTerm lengthFive yearsFormation10 October 1940; 83 years ago (1940-10-10)First holderC...

Melodifestivalen 2016 Type Pré-sélection pour le Concours Eurovision de la chanson Création 1959 Édition 56e Pays Suède Localisation Friends Arena, Stockholm Organisateur Sveriges Television (SVT) Date Demi-finales :6 février 201613 février 201620 février 201627 février 2016Andra Chansen :5 mars 2016Finale :12 mars 2016 Participant(s) 28 artistes (7 artistes dans chaque demi-finale) Site web Site officiel Melodifestivalen 2015 Melodifestivalen 2017 modifier Le M...
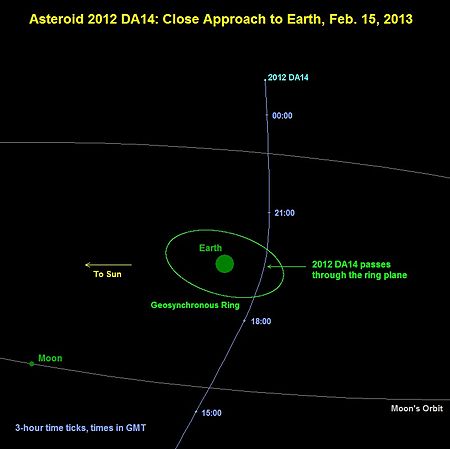
2012 DA14Diagram 2012 DA14 melewati Bumi pada 15 Februari 2013Penemuan[1]Ditemukan olehObservatorium OAM, La Sagra (J75)Reflektor 0,45-mTanggal penemuan23 Februari 2012PenamaanPenamaan2012 DA14Kategori planet minorPra-2013: Apollo NEO[2]Setelah 15 Feb 2013: Aten[2]Ciri-ciri orbit[3]Epos 30 Sep 2012Aphelion1,110 SA (Q)Perihelion0,8935 SA (q)Sumbu semimayor1,001 SA (a)Eksentrisitas0,1081Periode orbit366,2 hariAnomali rata-rata299,9° (M)Inklinasi10...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

銮披汶·頌堪แปลก พิบูลสงคราม第3任泰國總理任期1938年12月16日—1944年8月1日君主國王拉玛八世前任披耶帕凤侯爵继任寬·阿派旺第8任泰國總理任期1948年4月8日—1957年9月16日君主國王拉玛九世前任寬·阿派旺继任乃朴·沙拉信 个人资料出生貝·基達桑卡(1897-07-14)1897年7月14日 暹罗暖武里府逝世1964年6月11日(1964歲—06—11)(66歲) 日本神奈川縣相模原市国籍&#...

李光耀逝世及葬礼李光耀(1923年-2015年)日期2015年3月23日-2015年3月29日地点新加坡斯里淡马锡(私人守灵)新加坡国会大厦(民众瞻仰)新加坡国立大学文化中心(国葬)万礼火葬场(英语:Mandai Crematorium and Columbarium)(火葬)网站www.rememberingleekuanyew.sg 2015年3月23日凌晨3時18分(新加坡標準時間),新加坡建国后首任总理、前內閣资政和执政人民行动党首任秘书长李光�...

كول بالمر (بالإنجليزية: Cole Palmer) معلومات شخصية الميلاد 6 مايو 2002 (العمر 22 سنة)[1] الطول 1.89 م (6 قدم 2 1⁄2 بوصة) مركز اللعب لاعب وسط هجومي [لغات أخرى]، وجناح [لغات أخرى] الجنسية المملكة المتحدة معلومات النادي النادي الحالي تشيل�...

KombuchaJenisminuman fermentasi, minuman ringan dan teh AsalTiongkok Komposisiteh, gula dan SCOBY [sunting di Wikidata]lbs Kombucha adalah teh jamur yang berasal dari Asia Timur dan tersebar ke Jerman melalui Rusia sekitar pergantian abad ke-20. Penyembuh berbagai macam penyakit ini semakin banyak digunakan di rumah tangga dalam berbagai negara di Asia. Jamur kombucha merupakan membran jaringan-jamur yang bersifat gelatinoid dan liat, serta berbentuk piringan datar. Kombucha hidup dalam l...

A21高速公路道路信息道路總長57.6公里(35.8英里)启用时间1971公路系統法国高速公路 A21高速公路是法国西北部的一条免费高速公路,又称“Rocade Minière”。目前,Flers-en-Escrebieux到Pecquencourt路段正在施工中。Pecquencourt到Douchy-les-Mines段有建设提议。 参考资料 Saratlas上的资料(页面存档备份,存于互联网档案馆) 查论编法国高速公路(英语:Autoroutes_of_France)一位数字 A1 A1(972) ...

The following is an incomplete list of works by Artemisia Gentileschi. Catalogue numbers abbreviated WB are taken from the 1999 publication by Raymond Ward Bissell,[1] and number abbreviated MET are from the 2001 publication by the Metropolitan Museum of Art. Other attributions are taken from Jesse Locker's The Language of Painting.[2][3] Further references are available on the Bibliography on Artemisia Gentileschi. image name year collection dimensions inventory nr. ...





































































![{\displaystyle u={\frac {GM}{\ell ^{2}}}{\bigg [}1+e\cos(\theta -\theta _{0}){\bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3686b6acff1d8c81ea20a93f138baed2235696fc)


