Integral impròpia
|
Read other articles:

Pour les articles homonymes, voir Néo-classique. La Rotunda Santa Marija de Mosta, à Malte, est construite à partir de 1833. L'architecture néo-classique est un courant architectural procédant du néo-classicisme de la seconde moitié du XVIIIe siècle et du début du XIXe siècle. Succédant au classicisme, à l’architecture baroque et rococo, l'architecture néo-classique utilise les éléments gréco-romains (colonnes, fronton, proportions harmonieuses, portique) et s...

نيزافيسيمايا غازيتاНезависимая газета (بالروسية) الشعارمعلومات عامةالنوع معلومات بلد المنشأ روسيا[1] التأسيس 21 ديسمبر 1990 أول نشر 21 ديسمبر 1990 القطع A2 (en) موقع الويب ng.ru[2] شخصيات هامةالمالك Konstantin Remchukov (en) رئيس التحرير Konstantin Remchukov (en) التحريراللغة الروسية[1] المو...

Motor vehicle Renault TNA Renault TNH4 of 1937OverviewTypeTransit busManufacturerRenaultProduction1931–1971AssemblyBoulogne-Billancourt, FranceBody and chassisLayoutFront-engine, rear-wheel drivePowertrainTransmission4-speed manualChronologyPredecessorRenault PN The Renault TN is a range of buses produced from 1931 until 1971 for the Paris service. They have been described by Le Monde as a symbol of a Paris era.[1] History In 1931, the first TN model, the TN4, a bus with a length of...

Pour les articles homonymes, voir Réalisme. En philosophie, le réalisme désigne la position qui affirme l’existence d’une réalité extérieure indépendante de notre esprit. Le réalisme affirme à la fois l’existence et l’indépendance du monde[1]. L’existence signifie qu’il y a un monde extérieur au sujet, et l’indépendance, que ce monde n’a pas besoin d’être relié à un sujet pour exister. Le réalisme affirme que le monde est une chose et que nos représentation...

Dutch speed skater Eppie BleekerBleeker in 1974Personal informationBorn5 May 1949 (1949-05-05) (age 74)Bolsward, NetherlandsSportCountry NetherlandsSportSpeed skating Medal record World Sprint Championships 1973 Oslo Sprint 1974 Innsbruk Sprint Eppie Bleeker (born 5 May 1949) is a retired Dutch speedskater who won bronze medals at the World Sprint Championships in 1973 and 1974. He also won the national sprint titles in 1974 and 1975.[1] Personal bests:[2] 500 m...

Provinsi Laguna merupakan sebuah provinsi di Filipina. Ibu kotanya ialah Santa Cruz. Provinsi ini terletak di region CALABARZON. Provinsi ini memiliki luas wilayah 1.823,6 km² dengan memiliki jumlah penduduk 2.737.033 jiwa (2010) atau 542.906 rumah tangga. Dengan memiliki angka kepadatan penduduk 1.501 jiwa/km². Pembagian wilayah Secara administratif wilayah provinsi Laguna terbagi menjadi 24 munisipalitas dan 6 kota komponen, yaitu: Alaminos Bay Biñan Cabuyao Calamba Calauan Cavinti...

此條目可能包含不适用或被曲解的引用资料,部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队(军事) 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 ...

German-born film producer (1889–1966) Erich Pommer (left) with Carl Zuckmayer and Emil Jannings (1929) Erich Pommer (20 July 1889 – 8 May 1966) was a German-born film producer and executive. Pommer was perhaps the most powerful person in the German and European film industries in the 1920s and early 1930s.[1] As producer, Erich Pommer was involved in the German Expressionist film movement during the silent era. As the head of production at Decla Film, Decla-Bioskop, and, from 1924...
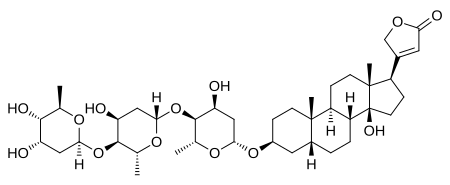
Naturally occurring steroids that are found in plants See also: Phytosterol Digitoxin, a phytosteroid and cardiac glycoside found in digitalis. Phytosteroids, also known as plant steroids, are naturally occurring steroids that are found in plants.[1] Examples include digoxin, digitoxin, diosgenin, and guggulsterone, as well as phytosterols like β-sitosterol and other phytoestrogens like isoflavones.[1] References ^ a b Hugh L. J. Makin; D.B. Gower; B. Kirk (29 June 2013). Ste...

Questa voce sull'argomento meccanica è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Questa voce o sezione sull'argomento meccanica non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. La tecnologia TSI (Turbocharged Stratified Injection) o TFSI (Turbocharged Fuel Stratified Injection) è un sistema, utilizzato dal gru...

Gambia Football FederationDisciplina Calcio Fondazione1952 Nazione Gambia ConfederazioneFIFA (dal 1966)CAF (dal 1966) Sede Banjul Presidente Seedy Kinteh Sito ufficialegambiaff.org/ Modifica dati su Wikidata · Manuale La Federazione calcistica del Gambia (ing. Gambia Football Federation, acronimo GFF) è l'ente che governa il calcio in Gambia. Fondata nel 1952, si affiliò alla FIFA e alla CAF nel 1966. Ha sede nella capitale Banjul e controlla il campionato nazionale, la coppa naz...

Discontinued series of high-end phones by Nokia Nokia NseriesManufacturerNokiaSeriesNseriesCompatible networksGSM, EDGE, UMTS, HSPAAvailability by region2005–2011RelatedNokia LumiaOperating systemSymbian, Maemo, MeeGo/HarmattanRemovable storageMicroSDRear camera2.0–12.0 MPFront camera0.3 MP / VGA / Common Intermediate Format-5 MPConnectivityWLANDevelopment statusDiscontinued The Nokia Nseries was a high-end lineup of feature phones, smartphones, and tablets marketed by Nokia Corporation f...

القوات الجوية المصرية شعار القوات الجوية المصرية الدولة مصر الإنشاء 1930 (كجزء من القوات المسلحة). 1937 (كسلاح مستقل). النوع سلاح الجو الدور حماية سماء مصر وتأمين مجالها الجوي الحجم 30,000 في الخدمة (2014 في)[1]20,000 الاحتياط (في 2014)[1]50,000 المجموع (في 2014)[1]1,136 الطائرات (�...

Giuliano SimeoneNazionalità Argentina Altezza173 cm Peso75 kg Calcio RuoloAttaccante Squadra Atlético Madrid CarrieraGiovanili 2014-2018 River Plate2018-2022 Atlético Madrid Squadre di club1 2021-2022 Atlético Madrid B51 (29)2022 Atlético Madrid1 (0)2022-2023→ Real Saragozza36 (9)2023-2024→ Alavés6 (1)2024- Atlético Madrid0 (0) 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campionato.Il simbolo → indic...

Donna LewisDonna pada tahun 2009Lahir(1959-08-00)Agustus 1959[1]Cardiff, WalesPekerjaan Komposer penyanyi pianis produser Tahun aktif1970s—Karier musikGenre Dance-Pop Dream Pop Folk Pop Instrumen Kibor piano vokal LabelAtlanticSitus web[1] Donna Lewis (lahir Agustus 1959) adalah seorang penyanyi berkebangsaan Wales. Dia terkenal lewat lagu I Love You Always Forever. Di Billboard Hot 100, lagu itu berada di posisi kedua selama sembilan pekan, ditahan dari posisi jawara oleh lag...

「中村駿介」、「中村駿介 (バレーボール)」、あるいは「中村俊介 (曖昧さ回避)」とは別人です。 中村 俊輔 RCDエスパニョール時代(2009年)名前愛称 俊輔、俊さん、シュン[1]、NAKA(ナカ)[1]カタカナ ナカムラ シュンスケラテン文字 NAKAMURA Shunsuke基本情報国籍 日本生年月日 (1978-06-24) 1978年6月24日(46歳)出身地 神奈川県横浜市戸塚区身長 178cm体重 71kg選手�...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (يوليو 2020) هذه القائمة غير مكتملة. فضلاً ساهم في تطويرها بإضافة مزيد من المعلومات ولا تنسَ الاستشهاد بمصادر موثوق به�...

Transformation of the chemical structure of a molecule or ion In chemistry, isomerization or isomerisation is the process in which a molecule, polyatomic ion or molecular fragment is transformed into an isomer with a different chemical structure.[1] Enolization is an example of isomerization, as is tautomerization.[2] When the isomerization occurs intramolecularly it may be called a rearrangement reaction.[citation needed] When the activation energy for the isomerizati...

ぽてまよ ジャンル ギャグ 漫画 作者 御形屋はるか 出版社 双葉社 掲載誌 もえよん → コミックハイ! レーベル アクション・コミックス 発表期間 2004年7月9日 - 2011年1月22日 巻数 全5巻 アニメ 原作 御形屋はるか 監督 池端隆史 シリーズ構成 池見友太 脚本 池見友太 キャラクターデザイン 大木良一 音楽 菊谷知樹 アニメーション制作 J.C.STAFF 製作 ぽてまよ製作委員会 放�...

British neo-Fascist organisation League of Saint George League of St George EmblemFounderKeith ThompsonMike GriffinFounded1974Split fromAction PartyNewspaperThe League ReviewThe League SentinelMembership (1970s)50–100IdeologyBritish fascismEurope a NationPolitical positionFar-rightPolitics of the United KingdomPolitical partiesElections The League of St George is a neo-fascist organisation based in the United Kingdom. It has defined itself as a non-party, non-sectarian political c...









![{\displaystyle \int _{0}^{1}{\frac {1}{\sqrt {x}}}dx={\underset {h\to 0}{\mathop {\lim } }}\,\int _{h}^{1}{\frac {1}{\sqrt {x}}}dx={\underset {h\to 0}{\mathop {\lim } }}\,\left[2{\sqrt {x}}\right]_{h}^{1}=2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8571ee2d943ba0261e0f8358ad8d4dfc524a49c)

![{\displaystyle \int _{0}^{1}{\frac {1}{x}}dx={\underset {h\to 0^{+}}{\mathop {\lim } }}\,\int _{h}^{1}{\frac {1}{x}}dx={\underset {h\to 0^{+}}{\mathop {\lim } }}\,\left[\ln \left(x\right)\right]_{h}^{1}=\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a3ab64d3403a5e35a22d0338b14f9354fa7cea8)











