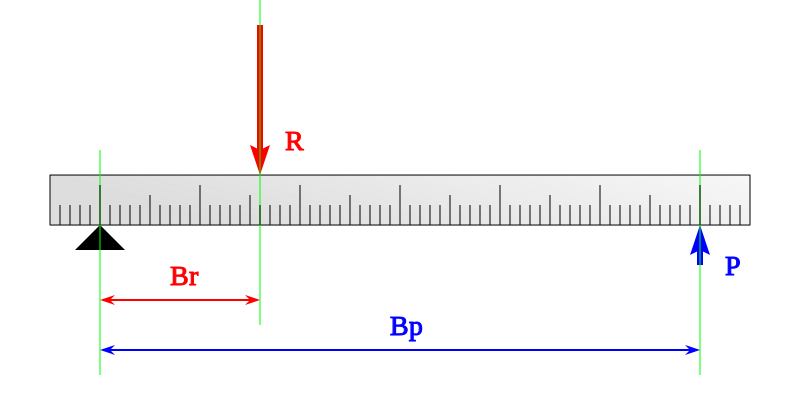
Avantatge mecànic
|
Read other articles:

Direktorat JenderalBina Keuangan Daerah Kementerian Dalam Negeri Republik IndonesiaGambaran umumDibentuk12 Mei 2004Dasar hukumKeputusan Presiden Nomor 88 Tahun 2003Pegawai233 OrangAlokasi APBNAPBNSusunan organisasiDirektur JenderalHoras Maurits PanjaitanSekretaris Direktorat JenderalMauritz Panjaitan[1] DirektoratPerencanaan Anggaran DaerahBahri[1]Pelaksanaan dan Pertanggungjawaban Keuangan DaerahRikie[1]Fasilitasi Dana Perimbangan dan Pinjaman DaerahSumule Tumbo[1...

خريطة لجميع الإحداثيات من جوجل خريطة لجميع الإحداثيات من بينغ تصدير جميع الإحداثيات من كيه إم إل تصدير جميع الإحداثيات من جيو ر س س خريطة لجميع الإحداثيات الميكرو منسقة بيانات من إطار توصيف الموارد تمتلك روسيا 26 موقعاً مسجلة لدى اليونسكو كمواقع تراث عالمي.[1] ستة عشر م�...

Basilika Santo KlemensBasilika Minor Santo KlemensJerman: Propsteikirche Basilika St. Clemenscode: de is deprecated Basilika Santo KlemensBasilika Santo Klemens52°22′23″N 9°43′36″E / 52.37306°N 9.72667°E / 52.37306; 9.72667Koordinat: 52°22′23″N 9°43′36″E / 52.37306°N 9.72667°E / 52.37306; 9.72667LokasiGoethestraße 33Hanover, Lower SaxonyNegara JermanDenominasiGereja Katolik RomaSitus webwww.st-clemens-hannover.deSej...

Dans le groupe des géosciences, la géotechnique est la technoscience consacrée à l’étude pratique de la subsurface terrestre sur laquelle notre action directe est possible pour son aménagement et/ou son exploitation, lors d’opérations de BTP (génie civil, bâtiment, carrières), de gestion des eaux souterraines (exploitation, drainage) et de prévention des risques naturels. Dans la pratique actuelle, il est indispensable d’y recourir lors de l’étude, la construction, la main...

The Beistle CompanyIndustryManufacturingDistributionFounded1900; 124 years ago (1900)FoundersMartin Luther BeistleHeadquartersShippensburg, Pennsylvania, U.S.[1]Key peopleHenry E. LuhrsWebsitebeistle.com The Beistle Company, or simply Beistle, is an American company known for manufacturing holiday decorations and party goods, and particularly known for its catalog of Halloween decorations. Beistle was founded in 1900 in Pennsylvania by Martin Luther Beistle, who crea...

For the English cricketer, see Philip Whitehead (cricketer). This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (March 2017) (Learn how and when to remove this template message) Phillip WhiteheadWhitehead in 1992Member of Parliament for Derby NorthIn office18 June 1970 – 13 May 1983Preceded byNiall MacDermotSucceeded ...

This article has an unclear citation style. The references used may be made clearer with a different or consistent style of citation and footnoting. (January 2024) (Learn how and when to remove this template message) Karl Trautmann (born 26 April 1932) is an East German former football manager and footballer who last managed SpVg Aurich. Career Trautmann helped East German side 1. FC Frankfurt reach the final of the 1976 FDGB-Pokal and helped East German side Eisenhüttenstädter FC Stahl rea...

Hubungan Indo-Amerika India Amerika Serikat Misi diplomatik Kedutaan Besar India di Washington, D.C. Kedutaan Besar Amerika Serikat di New Delhi di New Delhi Utusan Kedutaan Besar Navtej Sarna Kedutaan Besar Q QA and wa Vacant Kedutaan Besar India di Washington, D.C. Kedutaan Besar AS di New Delhi Hubungan Amerika Serikat dengan India (atau hubungan Indo-Amerika) merupakan hubungan Internasional antara Republik India dan Amerika Serikat. Tokoh terkemuka gerakan kebebasan di India memiliki hu...

First British satellite Ariel 1Scale model of Ariel 1 satellite, London Science MuseumNamesUK-1, S-55Mission typeIonosphericOperatorSERC / NASA[1]Harvard designation1962 Omicron 1[2]COSPAR ID1962-015A SATCAT no.285[1] Spacecraft propertiesManufacturerGoddard Space Flight CenterLaunch mass62 kilograms (137 lb) Start of missionLaunch date26 April 1962, 18:00:00 (1962-04-26UTC18Z) UTCRocketThor DM-19 DeltaLaunch siteCape Canaveral LC-17A End of mis...

Questa voce sugli argomenti aziende olandesi e reti televisive è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Nederlandse Omroep StichtingLogo Stato Paesi Bassi Forma societariaazienda pubblica Fondazione1957 Sede principaleHilversum SettoreMedia Sito webwww.nos.nl/ Modifica dati su Wikidata · Manuale Nederlandse Omroep Stichting o NOS è una delle aziende pubbliche che compongono la radiot...

هذه المقالة عن المجموعة العرقية الأتراك وليس عن من يحملون جنسية الجمهورية التركية أتراكTürkler (بالتركية) التعداد الكليالتعداد 70~83 مليون نسمةمناطق الوجود المميزةالبلد القائمة ... تركياألمانياسورياالعراقبلغارياالولايات المتحدةفرنساالمملكة المتحدةهولنداالنمساأسترالي�...

American voice actor and radio personality (1908–1989) Mel BlancBlanc in 1959BornMelvin Jerome Blank(1908-05-30)May 30, 1908San Francisco, California, U.S.DiedJuly 10, 1989(1989-07-10) (aged 81)Los Angeles, California, U.S.Resting placeHollywood Forever CemeteryOther namesThe Man of 1000 VoicesOccupation(s)Voice actor, radio personalityYears active1927–1989Spouse Estelle Rosenbaum (m. 1933)ChildrenNoel BlancAwardsInkpot Award (1976)[1]...

DC Comics supervillain team Crime Syndicate of AmericaThe original Crime Syndicate of America, as they appeared on a splash page of Convergence: Crime Syndicate #1 (April 2015). Art by Phil Winslade (pencils and inks) and Lovern Kindzierski (colors).Publication informationPublisherDC ComicsFirst appearance Crime Syndicate of America: Justice League of America #29 (August 1964) Crime Syndicate of Qward: Justice League International Quarterly #8 (Autumn 1992) Crime Syndicate of Amerika: JLA: Ea...

This article describes the 50th album in the U.S. Now! series. It should not be confused with identically-numbered albums from other Now! series. For more information, see Now That's What I Call Music! 50 and Now That's What I Call Music! discography. 2014 compilation album by Various artistsNow That's What I Call Music! 50Compilation album by Various artistsReleasedMay 6, 2014 (2014-05-06)Length76:43LabelUniversal Music EnterprisesNumbered series chronology Now That's ...

Minority religion in the country of New Zealand Islam by countryWorld percentage of Muslims by country Africa Algeria Angola Benin Botswana Burkina Faso Burundi Cameroon Cape Verde Central African Republic Chad Comoros Democratic Republic of the Congo Republic of the Congo Djibouti Egypt Equatorial Guinea Eritrea Eswatini Ethiopia Gabon Gambia Ghana Guinea Guinea-Bissau Ivory Coast Kenya Lesotho Liberia Libya Madagascar Malawi Mali Mauritania Mauritius Mayotte Morocco Western Sahara Mozambiqu...

Frecciarossa 1000 Elettrotreno Frecciarossa 1000 in sosta a Milano Centrale Anni di progettazione 2010-2012 Anni di costruzione Dal 2013[1] Anni di esercizio Dal 14 giugno 2015 Quantità prodotta 94 convogli (57 in esercizio, 1 incidentato, 36 in costruzione+10 opzionali la cui costruzione potrebbe essere confermata da Trenitalia nei prossimi anni[2] in costruzione) Costruttore AnsaldoBreda (dal 2015 Hitachi Rail Italy)Bombardier Transportation Italy (fino al 2020)Alstom (dal...

This is a list of airlines which have an air operator's certificate issued by the Civil Aviation Authority of Venezuela.[1][2] Airline Image IATA ICAO Callsign Hub airport(s) Founded Notes Aeroandinas [3] ARD CORDILLERAS La Fría 2012 Aerolíneas Estelar E4 ETR ESTELAR Caracas 2008 Aeroparaguaná Las Piedras 2013 Virtual airline Aeropostal Alas de Venezuela CW ALV AEROPOSTAL Caracas 1929 Aerotecnica [4] DUG ATSA Caracas 1951 Continues operations with smaller e...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Virginia Union Panthers football – news · newspapers · books · scholar · JSTOR (January 2024) Football program representing Virginia Union University Virginia Union Panthers football2024 Virginia Union Panthers football team First season1899Athletic d...

Rock surface indicating a gap in the geological record Hutton's Unconformity at Jedburgh, Scotland, illustrated by John Clerk in 1787 and photographed in 2003. An unconformity is a buried erosional or non-depositional surface separating two rock masses or strata of different ages, indicating that sediment deposition was not continuous. In general, the older layer was exposed to erosion for an interval of time before deposition of the younger layer, but the term is used to describe any break i...

Ala'a Abu Saleh Informasi pribadiNama lengkap Ala'a Abu SalehTanggal lahir 25 Juni 1987 (umur 37)Tempat lahir Sakhnin, IsraelPosisi bermain BekInformasi klubKlub saat ini Bnei SakhninNomor 8Karier senior*Tahun Tim Tampil (Gol)2005– Bnei Sakhnin 185 (9) * Penampilan dan gol di klub senior hanya dihitung dari liga domestik dan akurat per 15 Mei 2014 Ala'a Abu Saleh (juga dikenal sebagai Alaa; lahir 25 Juni 1987) adalah pemain sepak bola Arab-Israel. Dia bermain sebagai bek untuk Bn...