Foton

Portal "Fizika"
Odjeljak posvećen isključivo fizici
Fotoni emitovani u koherentnom snopu pomoću lasera

Fotoni su elementarne čestice[1][2][3][4] koje se mogu opisati kao elektromagnetni energetski paketi određene frekvencije. Primjer fotona je svjetlost, pored ostalih vidova elektromagnetnih talasa (radio zračenja, infra-crvenog zračenja, itd.). Fotoni imaju osobine zbog kojih se ova čestica smatra dijelom kao čestica, ali i kao talas, u nauci poznato kao dualitet čestice-talasa. Osobine zbog kojih se foton ponaša kao čestica su primjetljive u fotoelektričnom efektu, dok su osobine zbog kojih se smatra kao talas primjetne kroz difrakciju i interferiranje svjetla kroz otvor ili rupu. 1801. godine engleski naučnik Thomas Young dokazao je osobinu svjetlosti (fotona) da se ponaša poput talasa time što je, u principu, osvijetlio dupli otvor (engleski: double-slit). Rezultat ovog eksperimenta su bile linije na pozadini na kojoj se vidjelo svjetlo koje je prošlo kroz otvor. Intenzitet svjetla je bio najveći u sredini i slabio je simetrično sa obje strane. Ovo je bio prvi dokaz da svjetlo ima osobine talasa.

Svako tijelo na temperaturama većim od 0 K (kelvina) zrači elektromagnetne talase, koji se sastoje od čestica. Kada je u pitanju svjetlosno zračenje, tada se te čestice nazivaju fotoni.

Energija jednog fotona je proporcionalna frekvenciji svjetlosti (ε = hν).

  • ε (epsilon) – energija čestice(fotona)
  • h – Plankova (Max Planck) konstanta
  • ν (ni) – frekvencija svjetlosti

Također pogledajte

Reference

  1. ^ "Elementary particles". abyss.uoregon.edu. Arhivirano s originala, 30. 8. 2011. Pristupljeno 21. 11. 2019.
  2. ^ "What Is Elementary-Particle Physics?INTRODUCTION".
  3. ^ "Physics for Kids: Elementary Particles - Quarks, Bosons, Leptons". www.ducksters.com. Pristupljeno 21. 11. 2019.
  4. ^ Science, Adam Mann 2019-05-07T19:53:21Z Pure. "What Are Elementary Particles?". livescience.com (jezik: engleski). Pristupljeno 21. 11. 2019.

Vanjski linkovi

Commons logo
Commons logo
Commons ima datoteke na temu: Foton

Read other articles:

Pertu

PertuAwatara Wisnu sebagai maharaja pertama yang memulihkan keadaan di muka bumi dan mensejahterakan duniaEjaan DewanagariपृथुEjaan IASTPṛthuGolonganManusia awataraSenjataPanahKitabPuranaPasanganArcisaKeturunanWijitaswa, Haryaksa, Dumrakesa, Wreka dan Drawinalbs Dalam ajaran agama Hindu, Pertu (Sanskerta: पृथु ; Pṛ(ri)thu) adalah salah satu awatara Wisnu. Ia merupakan putra Wena. Ia menjadi suami Arcisa, dan bapak bagi Wijitaswa, Haryaksa, Dumrakesa, Wreka dan Drawina...

 

Associazione Calcio Cuneo 1905 2011-2012

Questa voce sull'argomento stagioni delle società calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: Associazione Calcio Cuneo 1905. Associazione Calcio Cuneo 1905Stagione 2011-2012Sport calcio Squadra Cuneo Allenatore Ezio Rossi Presidente Marco Rosso Seconda Divisione3º posto nel girone A. Promosso in Prima Divisione. Maggiori presenzeCampionato: Passerò (37...

 

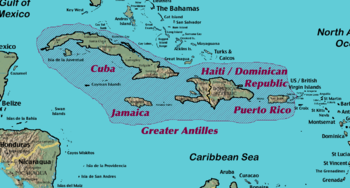
Grandes Antilles

Pour les articles homonymes, voir Antilles (homonymie). Carte des Grandes Antilles Les Grandes Antilles sont un groupe de quatre archipels formant quatre États indépendants des Antilles auxquels s'ajoutent Porto Rico et les îles Vierges (des États-Unis et britanniques), groupe nommé ainsi par opposition avec celui des Petites Antilles. Il s'agit par ordre de taille des îles de : Cuba, Hispaniola[1] (rassemblant la République d'Haïti et la République dominicaine), la Jamaïque, ...

Surgana State

Subdivision of British India Surgana StatePrincely State of British IndiaLate 18th century–1948 Flag Coat of arms Surgana State in Nasik Agency during British IndiaCapitalSurganaDemonymMaratha[1][2][3]Area • 1901932.4 km2 (360.0 sq mi)Population • 1901 11,532• 1921 14,912 Legislature • Upper housePawarHistory • Established Late 18th century• Independence of India 1948 Succeeded by India Toda...

 

Dutch Dehnert

Questa voce sugli argomenti allenatori di pallacanestro statunitensi e cestisti statunitensi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti dei progetti di riferimento 1, 2. Dutch Dehnert Nazionalità  Stati Uniti Altezza 185 cm Peso 95 kg Pallacanestro Ruolo Ala, centroAllenatore Termine carriera 1939 - giocatore1949 - allenatore Hall of fame Naismith Hall of Fame (1969) CarrieraSquadre di club 1920-1921 Original ...

 

Associazione Calcio Rondinella Marzocco Firenze 1985-1986

Voce principale: Rondinella Marzocco. Associazione Calcio Rondinella Marzocco FirenzeStagione 1985-1986Sport calcio Squadra Rondinella Marzocco Allenatore Paolo Ferrario poi Claudio Merlo Presidente Ugo Poggi Serie C110º posto nel girone A. Maggiori presenzeCampionato: Di Curzio (34) Miglior marcatoreCampionato: Fasolo (9) 1984-1985 1986-1987 Si invita a seguire il modello di voce Questa pagina raccoglie le informazioni riguardanti la Rondinella Marzocco nelle competizioni ufficiali de...

أتراك

هذه المقالة عن المجموعة العرقية الأتراك وليس عن من يحملون جنسية الجمهورية التركية أتراكTürkler (بالتركية) التعداد الكليالتعداد 70~83 مليون نسمةمناطق الوجود المميزةالبلد  القائمة ... تركياألمانياسورياالعراقبلغارياالولايات المتحدةفرنساالمملكة المتحدةهولنداالنمساأسترالي�...

 

Mickey au Camp de Gurs

1942 French comic book by Horst Rosenthal Mickey au Camp de Gurs(Mickey Mouse in the Gurs Internment Camp)Cover of Mickey au Camp de GursCreatorHorst RosenthalDate1942Main charactersMickey MousePage count15 pagesOriginal publicationPublished inMickey à Gurs: Les Carnets de dessin de Horst Rosenthal(Mickey in Gurs: The comic books of Horst Rosenthal)Date of publication2014LanguageFrenchISBN978-27021-438-5-8 Mickey au Camp de Gurs (Mickey Mouse in the Gurs Internment Camp)[1]...

 

Філософія

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

Resolusi 709 Dewan Keamanan Perserikatan Bangsa-Bangsa

Resolusi 709Dewan Keamanan PBBLokasi EstoniaTanggal12 September 1991Sidang no.3.007KodeS/RES/709 (Dokumen)TopikPenambahan anggota baru PBB: EstoniaHasilDiadopsiKomposisi Dewan KeamananAnggota tetap Tiongkok Prancis Britania Raya Amerika Serikat Uni SovietAnggota tidak tetap Austria Belgia Pantai Gading Kuba Ekuador India Rumania Yaman Zaire Zimbabwe Resolusi Dewan Keamanan Perserikatan Bangsa-Bangsa 709, diad...

 

elektron valensi

Empat ikatan kovalen. Karbon memiliki empat elektron valensi sehingga valensinya adalah empat. Masing-masing atom hidrogen memiliki satu elektron valensi dan disebut univalen. Dalam ilmu kimia, elektron valensi atau elektron harkat adalah elektron pada kelopak terluar yang terhubung dengan suatu atom, dan dapat berpartisipasi dalam pembentukan ikatan kimia jika kelopak terluar belum penuh. Dalam ikatan kovalen tunggal, kedua atom yang berikatan menyeimbangkan satu elektron valensi untuk membe...

 

Lotus 107

Lotus 107Mika Häkkinen nel Gran Premio di Gran Bretagna 1992Descrizione generaleCostruttore  Lotus Cars CategoriaFormula 1 SquadraTeam Lotus Progettata daChris Murphy SostituisceLotus 102 Sostituita daLotus 109 Descrizione tecnicaMeccanicaTelaioMonoscocca in fibra di carbonio Motore1992-1993: Ford-Cosworth HB 3.5 V81994: Mugen Honda MF-351H 3.5 V10 TrasmissioneCambio semiautomatico a 6 marce Dimensioni e pesiPeso515 kg AltroCarburante1992:BP1992-1993:Castrol1994:Mobil 1 PneumaticiGoodye...

New Zealand Davis Cup team

Tennis team representing New Zealand New ZealandCaptainKelly EverndenITF ranking39 1 (20 September 2021)ColorsBlack and WhiteFirst year1924 (1905 as Australasia)Years played68Ties played (W–L)134 (64–70)Years inWorld Group8 (5–8)Best finishSF (1982)Most total winsOnny Parun (30–32)Most singles winsJose Statham (24)Most doubles winsJames Greenhalgh (11–2)Best doubles teamBrett Steven/James Greenhalgh (6–1)Most ties playedJose Statham (27)Most years playedOnny Parun (15) The New Ze...

 

Industry Baby

Industry BabySingel oleh Lil Nas X featuring Jack Harlowdari album MonteroDirilis23 Juli 2021 (2021-07-23)Genre Trap pop rap Durasi3:32LabelColumbiaPencipta Montero Hill Jackman Harlow Mark Williams Raul Cubina Roy Lenzo Denzel Baptiste David Biral Kanye West Nick Lee[1] Produser Take a Daytrip Kanye West Kronologi singel Lil Nas X Sun Goes Down (2021) Industry Baby (2021) Thats What I Want (2021) Kronologi singel Jack Harlow I Won(2021) Industry Baby(2021) SUVs (Black ...

 

Henry George Jr.

American politician Henry George Jr.Member of theU.S. House of Representativesfrom New YorkIn officeMarch 4, 1911 – March 4, 1915Preceded byWilliam S. BennetSucceeded byG. Murray HulbertConstituency17th district (1911–13)21st district (1913–15) Personal detailsBornNovember 3, 1862Sacramento, California, USDiedNovember 14, 1916 (aged 54)Washington, D.C., USPolitical partyDemocratic Henry George Jr. (November 3, 1862 – November 14, 1916) was an American newspaperman who served ...

Quạ

QuạCorvus ossifragusPhân loại khoa họcGiới (regnum)AnimaliaNgành (phylum)ChordataLớp (class)AvesBộ (ordo)PasseriformesHọ (familia)CorvidaeChi (genus)CorvusL., 1758Loài điển hìnhCorvus coraxL., 1758 Các loài 45-46 loài, xem bài. Quạ (danh pháp: Corvus) là một chi chim thuộc họ Quạ (Corvidae).[1] Chi này có khoảng 45-46 loài có kích thước khác nhau. Các loài chim dạng quạ lớn nhất là quạ thường (Corvus corax) và quạ mỏ...

 

Mathematical analysis

Branch of mathematics Part of a series onMathematics History Index Areas Number theory Geometry Algebra Calculus and Analysis Discrete mathematics Logic and Set theory Probability Statistics and Decision theory Relationship with sciences Physics Chemistry Geosciences Computation Biology Linguistics Economics Philosophy Education Mathematics Portalvte A strange attractor arising from a differential equation. Differential equations are an important area of mathematical analysis with many applic...

 

Prime Minister of Yugoslavia

Head of government of the Yugoslav state Not to be confused with Prime Minister of Serbia and Montenegro. Prime Minister of YugoslaviaПремијер ЈугославијеPremijer JugoslavijeStandard of the Prime Minister(SFR Yugoslavia)Longest servingJosip Broz Tito2 November 1944 – 29 June 1963Government of YugoslaviaMember ofParliament of YugoslaviaReports toKing of Yugoslavia (Serbs, Croats and Slovenes) (1918–1945)President of Yugoslavia (1945–1971)Presidency of Yugoslavia (1971�...

Paper plane (cocktail)

Type of cocktail Paper planeIBA official cocktailTypeCocktailBase spirit Bourbon whiskey ServedStraight up: chilled, without iceStandard drinkware Cocktail glassIBA specifiedingredients† 30 ml Bourbon whiskey 30 ml Amaro Nonino 30 ml Aperol 30 ml fresh lemon juice PreparationPour all ingredients into cocktail shaker, shake well with ice, strain into chilled cocktail glass.† Paper plane recipe at International Bartenders Association The paper plane is a whiskey-based cocktail created in 20...

 

Zoe Tuckwell-Smith

Australian actress This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Zoe Tuckwell-Smith – news · newspapers · books · scholar · JSTOR (August 2013) (Learn how and when to remove this message) Zoe ...