Степенуване (математика)
|
Read other articles:

Hijau Laut Cahaya menembus permukaan dasar lautCommon connotationsAir laut Koordinat warnaTriplet hex#008080sRGBB (r, g, b)(0, 128, 128)CMYKH (c, m, y, k)(100, 0, 0, 50)HSV (h, s, v)(180°, 100%, 50[1]%)SumberDaftar Istilah WarnaWarna web X11[2]B: Dinormalkan ke [0–255] (bita)H: Dinormalkan ke [0–100] (ratusan) Hijau laut (Inggris: Teal, Bluish greencode: en is deprecated ) adalah suatu corak warna hijau kebir...

Disambiguazione – Se stai cercando altri significati, vedi Renault (disambigua). Questa voce o sezione sugli argomenti aziende dei trasporti e aziende francesi non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. RenaultLogo Stato Francia Forma societariaSocietà anonima Borse valoriEuronext: RNO ISINFR...

L. S. CousinsLance Selwyn Cousins, 2012.Lahir7 April 1942Hitchin, Britania RayaMeninggal14 Maret 2015 (usia 72) Lance Selwyn Cousins (7 April 1942 – 14 Maret 2015) adalah seorang cendekiawan utama dalam bidang kajian Buddha. Lahir di Hitchin, Hertfordshire, ia belajar sejarah dan kajian oriental di Universitas Cambridge[1] Referensi ^ oxford.academia.edu/LSCousins Pengawasan otoritas Umum Integrated Authority File (Jerman) ISNI 1 VIAF 1 WorldCat Perpustakaan nasional ...

Dunia dalam BeritaGenreBeritaNegara asalIndonesiaBahasa asliBahasa IndonesiaProduksiLokasi produksiStudio 4 TVRI, Jalan Gerbang Pemuda Senayan, Gelora, Tanah Abang, Jakarta Pusat, Daerah Khusus Ibukota JakartaDurasi10 menit (1978-1979)20 menit (1979-1982)30 menit (1982—sekarang)Rilis asliJaringan TVRI Sebelumnya: RCTI (13 November 1988—30 Juli 2000) SCTV (25 Agustus 1990—30 Juli 2000) TPI (23 Januari 1994—30 Juli 2000) ANteve (1 Maret 1993—30 Juli 2000) Indosiar (18 Desember 1994�...

Historic garden cemetery in Atlanta, Georgia, United States For other places with the same name, see Oakland Cemetery (disambiguation). United States historic placeOakland CemeteryU.S. National Register of Historic Places Oakland Cemetery with the Atlanta skyline in the backgroundShow map of AtlantaShow map of GeorgiaShow map of the United StatesLocation248 Oakland Avenue, SE, Atlanta, GeorgiaCoordinates33°44′55″N 84°22′17″W / 33.74861°N 84.37139°W / 33.748...

Type of classical male singing voice This article is about the male voice type. For other uses, see Bass. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Bass voice type – news · newspapers · books · scholar · JSTOR (February 2008) (Learn how and when to remove this template message) Voice type Female S...

Dan Eggen Nazionalità Norvegia Altezza 192 cm Calcio Ruolo Difensore Termine carriera 2005 Carriera Squadre di club1 1988 Lyn Oslo0 (0)1989 Årvoll? (?)1990 Ready? (?)1991-1993 Frem60 (13)1993-1997 Brøndby108 (6)1997-1999 Celta Vigo39 (2)1999-2004 Alavés40 (2)2003→ Rangers0 (0)2003-2005 Le Mans22 (1) Nazionale 1988 Norvegia U-181 (0)1991 Norvegia U-212 (0)1993-2001 Norvegia25 (2) Carriera da allenatore 2009-2011 KolbotnFemminile20...

Halaman ini berisi artikel tentang film karya Nicholas Hytner. Untuk film karya Raymond Rouleau, lihat The Crucible (film 1957). The CruciblePoster rilis teatrikalSutradaraNicholas HytnerProduserRobert A. MillerDavid V. PickerSkenarioArthur MillerBerdasarkanThe Crucibleoleh Arthur MillerPemeranDaniel Day-LewisWinona RyderPaul ScofieldJoan AllenBruce DavisonPeter VaughanPenata musikGeorge FentonSinematograferAndrew DunnPenyuntingTariq AnwarDistributor20th Century FoxTanggal rilis 27 Nove...

In this Chinese name, the family name is Shih. Morley ShihShih Mao-lin施茂林Minister of Justice of the Republic of ChinaIn office1 February 2005 – 19 May 2008DeputyLee Chin-yungPreceded byChen Ding-nanSucceeded byWang Ching-feng Personal detailsBorn (1950-08-02) 2 August 1950 (age 73)Chiayi, TaiwanAlma materNational Taiwan UniversityProfessionprosecutor and judge Morley Shih (Chinese: 施茂林; pinyin: Shī Màolín; born 2 August 1950) is a Taiwanese prosecutor a...

Untuk kegunaan lain, lihat Undine (disambiguasi). Undine karya John William Waterhouse (1849–1917), dipamerkan di Society of British Artists pada 1872.[1] Undine /ˈʌnˌdiːn, ˌʌnˈdiːn/ (atau ondine) adalah sebuah kategori hal elemental yang dikaitkan dengan air, yang mula-mula disebutkan dalam tulisan-tulisan alkemi Paracelsus. Makhluk serupa ditemukan dalam sastra klasik, terutama, Metamorphoses karya Ovid. Para penulis pada masa berikutnya mengembangkan undine menjadi nimfa ...
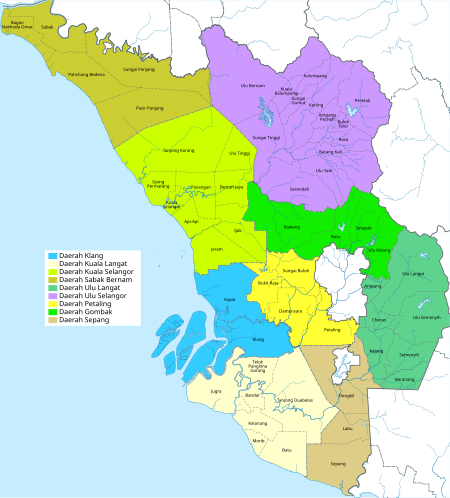
This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Bukit Beruntung – news · newspapers · books · scholar · JSTOR (April 2020) (Learn how and when to remove this message) Township in Hulu Selangor, Selangor, Malaysia Place in Selangor, MalaysiaBukit BeruntungBukit Beruntung InterchangeBukit BeruntungLocation in ...

Baseball or softball pitcher who throws the first pitch for their team in a game Chris Young warms up in the bullpen before a game at Wrigley Field minutes before the 12:05 start (see scoreboard clock). In baseball (hardball or softball), a starting pitcher or starter is the first pitcher in the game for each team. A pitcher is credited with a game started if they throw the first pitch to the opponent's first batter of a game. Starting pitchers are expected to pitch for a significant portion ...

Gerakan Hak-Hak Sipil Amerika beralih ke halaman ini. Untuk untuk periode sebelumnya, lihat Gerakan Hak-Hak Sipil Afrika-Amerika (1896–1954). Tokoh-tokoh utama Gerakan Hak Sipil Amerika-Afrika. Searah jarum jam dari kiri atas: W.E.B. Du Bois, Malcolm X, Rosa Parks, Martin Luther King, Jr. Gerakan Hak-Hak Sipil Afrika-Amerika (1955-1968) mengacu pada gerakan-gerakan di Amerika Serikat yang ditujukan untuk melarang diskriminasi rasial terhadap orang Afrika-Amerika dan memulihkan hak-hak suara...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

You can help expand this article with text translated from the corresponding article in Polish. (September 2011) Click [show] for important translation instructions. View a machine-translated version of the Polish article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wiki...

Hari Ulang Tahun Kaisar天皇誕生日Tennō tanjōbiPenduduk mengibarkan bendera di Istana Kekaisaran Tokyo pada hari ulang tahun Kaisar Akihito pada tahun 2017Nama resmiTennō tanjōbi (天皇誕生日)Nama lainTenchōsetsu (天長節) (−1948)Dirayakan oleh JepangJenisHari libur nasionalMaknaMemperingati hari lahir Kaisar JepangPerayaanUpacara publik di Istana Kekaisaran Tokyo, salam pembuka oleh kekaisaranTanggal23 FebruariFrekuensiTahunanHari Ulang Tahun Kaisar (天皇誕生日code...

Les élections législatives japonaises de 1917 (第13回衆議院議員総選挙, Dai-jusan Shūgiin Giinsōsenkyō?) sont les treizièmes organisées après l'avénement de l'empire du Japon et ont pour but d'élire les membres de la chambre des représentants de la Diète du Japon. Elles ont lieu le 20 avril 1917. Le Rikken Seiyūkai, mené par le premier ministre Terauchi Masatake, domine le Kenseikai (l'ancien Rikken Dōshikai) et obtient une majorité de sièges à la Diète. Résultats...

Een sporofyt is een generatie in de levenscyclus van een eukaryoot organisme dat sporen vormt. De sporen zijn haploïde of zelden diploïde. Haploïde sporen worden gevormd door meiose bij een (meio-)sporofyt; men spreekt hier ook van meiosporen. Dit komt het meeste voor. In enkele gevallen worden door mitose bij een sporofyt diploïde mitosporen gevormd. Een voorbeeld is hier het groenwier Cladophora glomerata. Levenscyclus Diplohaplont met digenetische cyclus kernfasen diplofase(2n) ...

Questa voce o sezione contiene informazioni riguardanti un film in produzione, atteso o annunciato. Il contenuto potrebbe cambiare radicalmente non appena maggiori informazioni saranno disponibili. Per favore, non aggiungere speculazioni alla voce. ElioElio in una scena del teaser trailerLingua originaleinglese Paese di produzioneStati Uniti d'America Anno2025 Genereanimazione, commedia, fantascienza, avventura, fantastico RegiaDomee Shi, Madeline Sharafian, Adrian Molina Sce...

European dynasty of German and Dutch origin House of Orange redirects here. For other uses, see House of Orange (disambiguation). House of Orange-NassauRoyal houseRoyal arms of the NetherlandsArms of William the SilentParent houseHouse of NassauCountryNetherlands, United Kingdom, Ireland, Luxembourg, Belgium, France, Germany, Orange, NassauEtymologyOrange, France & Nassau, GermanyFounded15 July 1544; 480 years ago (1544-07-15)FounderWilliam the SilentCurrent headKing Wil...










![{\displaystyle \;{\sqrt[{n}]{b}}=a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c2000bd65e9fd38e8148ddaf6a0688747059a91)







![{\displaystyle \;a^{\frac {1}{n}}={\sqrt[{n}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/078adab68f25f763668eb25ffefffc799aefbc4e)

![{\displaystyle \;a^{\frac {1}{3}}={\sqrt[{3}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b7dfd7b36b6d24593c2f5dee4aa81c52fcb5abb)



























![{\displaystyle \;7^{\frac {2}{3}}={\sqrt[{3}]{7^{2}}}=({\sqrt[{3}]{7}})^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/302f04e215beed5d1091285ae36c585269794bd4)
![{\displaystyle \;{\sqrt[{3}]{2^{3}}}=2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9101a09c9b1e2d0e619ad05fc58bd1ef3c3e9b56)
![{\displaystyle \;{\sqrt[{4}]{3^{4}}}=3}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ecd86b0ee55e364089487a5f50a603df4ead7fe)


![{\displaystyle \;{\sqrt[{3}]{8}}=8^{\frac {1}{3}}=2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1a5867e998258f3cddd56805f1203fe096a5427)
![{\displaystyle \;{\sqrt[{4}]{81}}=81^{\frac {1}{4}}=3}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfaa0eee9ef9c4d0ffe706a0a3f674236426fc76)
![{\displaystyle \;{\sqrt[{3}]{2^{3}}}={(2^{3})}^{\frac {1}{3}}={(2^{\frac {3}{1}})^{\frac {1}{3}}}=2^{{\frac {3}{1}}\times {\frac {1}{3}}}=2^{1}=2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4112969fa8d634681e6c842acf97753f547b7ea6)
![{\displaystyle \;{\sqrt[{4}]{(3)^{4}}}=(3^{4})^{\frac {1}{4}}=(3^{\frac {4}{1}})^{\frac {1}{4}}=3^{{\frac {4}{1}}\times {\frac {1}{4}}}=3^{1}=3}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99829c97ddbf29c48e948ca530f838cad5103bc9)



![{\displaystyle \;({\sqrt[{10}]{25}})^{5}=(25^{\frac {1}{10}})^{5}=25^{{\frac {1}{10}}\times {\frac {5}{1}}}=25^{\frac {1}{2}}={\sqrt {25}}=5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eba772f274c8e7e331e65edca5115c0d91bc23f6)

