Естествено число
|
Read other articles:

Часть серии статей о Холокосте Идеология и политика Расовая гигиена · Расовый антисемитизм · Нацистская расовая политика · Нюрнбергские расовые законы Шоа Лагеря смерти Белжец · Дахау · Майданек · Малый Тростенец · Маутхаузен ·&...

Commuter Line Bandung RayaB Commuter Line Bandung Raya Ekonomi persiapan memasuki Stasiun Bandung (atas), Commuter Line Bandung Raya tiba di Stasiun Haurpugur (bawah)Informasi umumJenis layananKereta api komuterStatusBeroperasiOperator saat iniKAI CommuterOperator sebelumnyaKereta Api IndonesiaJumlah penumpang harian35.256 (rerata hari biasa)39.949 (rerata akhir pekan)73.527 (puncak, 30 April 2023)[1]Situs webhttps://commuterline.idLintas pelayananStasiun awalPadalarang dan Purwakarta...

Australian politician The HonourableMichael KeenanMinister for Human ServicesIn office20 December 2017 – 29 May 2019Prime MinisterMalcolm TurnbullScott MorrisonPreceded byAlan TudgeSucceeded byStuart RobertMinister for Digital TransformationIn office20 December 2017 – 29 May 2019Prime MinisterMalcolm TurnbullScott MorrisonPreceded byAngus Taylor (as assistant minister)Succeeded byAbolishedMinister for JusticeIn office18 September 2013 – 20 December 2...

Запрос «Пугачёва» перенаправляется сюда; см. также другие значения. Алла Пугачёва На фестивале «Славянский базар в Витебске», 2016 год Основная информация Полное имя Алла Борисовна Пугачёва Дата рождения 15 апреля 1949(1949-04-15) (75 лет) Место рождения Москва, СССР[1]...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Abby the Spoon LadyAbby the Spoon Lady tampil di Asheville, North Carolina.Informasi latar belakangNama lahirAbby RoachLahir29 Oktober 1981 (umur 42)Wichita, Kansas, United StatesAsalWichita, Kansas, A.S.GenreAmerican folkPekerjaan pemusik Aktivi...

Leader of militant Tamil organisation in Sri Lanka (1954–2009) Prabhakaran redirects here. For the 2008 film, see Prabhakaran (film). This article is about a person whose name includes a patronymic. The article properly refers to the person by his given name, Prabhakaran, and not as Velupillai. Velupillai Prabhakaranவேலுப்பிள்ளை பிரபாகரன்Prabhakaran in 2006Born(1954-11-26)26 November 1954Valvettithurai, Dominion of Ceylon[1][2][3...

1989 filmCountdown to WarDirected byPatrick LauWritten byRonald HarwoodProduced byNorma PercyStarringIan McKellen, Michael Aldridge, Rashid Suhrawardy, Peter Vaughan, Alex Norton, David Swift, John WoodvineMusic byRichard HarveyRelease date 1989 (1989) Running time78 minutesLanguageEnglish Countdown to War is a television film made in 1989 as a co-production by Granada Television and PBS. It recounts the events that occurred between 15 March 1939, when the German army commanded by Adolf ...

Ohio gubernatorial election 1826 Ohio gubernatorial election ← 1824 10 October 1826 1828 → Nominee Allen Trimble Alexander Campbell Party National Republican Democratic-Republican Popular vote 71,475 4,765 Percentage 84.35% 5.62% Governor before election Jeremiah Morrow Democratic-Republican Elected Governor Allen Trimble National Republican Elections in Ohio Federal government U.S. President 1804 1808 1812 1816 1820 1824 1828 1832 1836 1840 1844 1848 1852 18...

Identification card used to enter the United States The front of the updated version of the Border Crossing Card A Border Crossing Card (BCC) is an identity document used by nationals of Mexico to enter the United States. As a standalone document, the BCC allows its holder to visit the border areas of the United States when entering by land or sea directly from Mexico for up to 30 days.[1][2] The document also functions as a B1/B2 visa when presented with a valid Mexican passp...
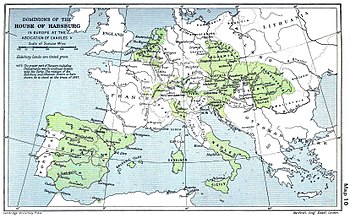
Wangsa HabsburgNegaraAustria, Kekaisaran Romawi Suci, Spanyol-Italia, Hungaria-Kroasia, Bohemia, Inggris-Irlandia (Jure uxoris), Portugal, Bosnia dan SloveniaKelompok etnisAustria, Katalan-Kastilia, PortugisDidirikanabad ke-12 - Pangeran Otto II dari HabsburgGelar Kaisar Romawi Kaisar Austria Raja Jerman Kaisar Meksiko Raja Spanyol Raja Aragon Raja Sisilia Kerajaan Napoli Raja Kastilia Raja Hungaria Raja Bohemia Raja Kroasia Raja Inggris dan Irlandia Raja Portugal Raja Dalmatia Raja Galisia d...

Canadian provincial election 1905 Saskatchewan general election ← 1902 (NWT) 13 December 1905 (1905-12-13) 1908 → ← outgoing membersmembers →25 seats in the Legislative Assembly of Saskatchewan13 seats needed for a majority First party Second party Leader Thomas Walter Scott Frederick W. A. G. Haultain Party Liberal Provincial Rights Leader since 16 August 1905 1905 Leader's seat Lumsden South Qu'Appelle Seats&...

Dewan regional (bahasa Ibrani: מועצה אזורית, Mo'atza Azorit; bahasa Inggris: Regional councils) merupakan salah satu dari tiga jenis lembaga pemerintah daerah di Israel dan daerah yang diduduki Israel. Kedua jenis lainnya adalah dewan kota dan dewan lokal. Sampai tahun 2003, terdapat 53 dewan regional, biasanya bertanggung jawab atas pemerintahan sejumlah pemukiman yang tersebar di area pedesaan.[1][2] Dewan regional terdiri dari perwakilan komunitas,...

2014 FIFA U-20女子ワールドカップFIFA U-20 Women's World Cup Canada 2014大会概要開催国 カナダ日程 2014年8月5日 - 8月24日チーム数 16 (6連盟)開催地数 4 (4都市)大会結果優勝 ドイツ (3回目)準優勝 ナイジェリア3位 フランス4位 北朝鮮大会統計試合数 32試合ゴール数 102点(1試合平均 3.19点)総入場者数 288,558人(1試合平均 9,017人)得点王 アシサト・...

Эта статья о афганской провинции; О афганском политике см. Вардак, Абдул Рахим. ВилайятВардагпушту وردګдари وردک 33°15′ с. ш. 66°00′ в. д.HGЯO Страна Афганистан Включает 8 районов Адм. центр Майданшахр История и география Площадь 8 938 км² (22-е место) Высота 2...

Elementary Calculus: An Infinitesimal Approach Second editionAuthorH. Jerome KeislerLanguageEnglishSubjectMathematicsPublisherDoverPublication date1976 Elementary Calculus: An Infinitesimal approach is a textbook by H. Jerome Keisler. The subtitle alludes to the infinitesimal numbers of the hyperreal number system of Abraham Robinson and is sometimes given as An approach using infinitesimals. The book is available freely online and is currently published by Dover.[1] Textbook Keisler...

First city-owned cannabis shop in Washington, US Cannabis CornerStevenson, WA, locationCompany typeShopIndustryCannabisFoundedMarch 7, 2015; 9 years ago (2015-03-07)Headquarters420 Evergreen Dr., North Bonneville, WA, USAWebsiteOfficial website Cannabis Corner is the first city-owned cannabis shop with its first location at 420 Evergreen Drive, North Bonneville, Washington, USA. As of 2020,[update] the main storefront is located in Stevenson, Washington. History The ...

Questa voce o sezione sull'argomento competizioni calcistiche non è ancora formattata secondo gli standard. Commento: La pagina non è formattata e dimensionata come previsto dal modello di voce - stagione di una divisione di un campionato di calcio.Devono essere utilizzati nelle classifiche i colori stabiliti per i lettori ipovedenti e daltonici approvati dal progetto;sostituite tutte le classifiche eliminando gli align = center inutili e non rimossi dal vecchio modello;sostituiti tut...

КоммунаТерм-МаньоакThermes-Magnoac Герб 43°18′00″ с. ш. 0°35′36″ в. д.HGЯO Страна Франция Регион Юг — Пиренеи Департамент Верхние Пиренеи Кантон Кастельно-Маньоак Мэр Пьер Лабе(2014—2020) История и география Площадь 10,83 км² Высота центра 266–416 м Часовой пояс UTC+1:00, летом UTC+2:0...

American economist (born 1941) William NordhausNordhaus in Stockholm, December 2018BornWilliam Dawbney Nordhaus (1941-05-31) May 31, 1941 (age 83)[2]Albuquerque, New Mexico, U.S.EducationYale University (BA, MA)Sciences PoMassachusetts Institute of Technology (PhD)AwardsBBVA Foundation Frontiers of Knowledge Award (2017)Nobel Memorial Prize in Economic Sciences (2018)Scientific careerFieldsEnvironmental economicsInstitutionsYale UniversityThesisA theory of endogenous technologica...

Community in Saskatchewan, Canada Wroxtonclass=notpageimage| Location of Wroxton in Saskatchewan Wroxton is an unincorporated community in Saskatchewan, located 41 km east of Yorkton, 42 km west of Roblin, Manitoba, and 40 km south of Kamsack at the intersection of Highway 8 and Highway 10. It is the seat of the Rural Municipality of Calder No. 241 in the Census Division 9. History St. Elia Church Church Plaque Wroxton is home to the Ukrainian Orthodox Church of St. Elia, a cul...




