 –ü–ĺ–ļ–į–∑–į–Ĺ–ł—ā–Ķ –≤ –Ķ–ī–ł–Ĺ —Ü–≤—Ź—ā —Ą–ł–≥—É—Ä–ł —Ā–į –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł.
–ü–ĺ–ļ–į–∑–į–Ĺ–ł—ā–Ķ –≤ –Ķ–ī–ł–Ĺ —Ü–≤—Ź—ā —Ą–ł–≥—É—Ä–ł —Ā–į –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł.
–ü–ĺ–ī–ĺ–Ī–ł–Ķ –Ķ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ–Ĺ —ā–Ķ—Ä–ľ–ł–Ĺ –∑–į —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ĺ–ł—ā–Ķ —Ą–ł–≥—É—Ä–ł –ī–į –ł–ľ–į—ā –Ķ–ī–Ĺ–į–ļ–≤–į —Ą–ĺ—Ä–ľ–į –Ī–Ķ–∑ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –ĺ—ā —Ä–į–∑–ľ–Ķ—Ä–ł—ā–Ķ. –Ē–≤–Ķ —Ą–ł–≥—É—Ä–ł F1 –ł F2 —Ā–Ķ –Ĺ–į—Ä–ł—á–į—ā –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł, –į–ļ–ĺ –ľ–Ķ–∂–ī—É —ā–ĺ—á–ļ–ł—ā–Ķ –ł–ľ —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į –≤–∑–į–ł–ľ–Ĺ–ĺ –Ķ–ī–Ĺ–ĺ–∑–Ĺ–į—á–Ĺ–ĺ –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ, –Ņ—Ä–ł –ļ–ĺ–Ķ—ā–ĺ –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł—Ź—ā–į –Ĺ–į —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł—Ź—ā–į –ľ–Ķ–∂–ī—É –≤—Ā—Ź–ļ–į –ī–≤–ĺ–Ļ–ļ–į —Ā—ä–ĺ—ā–≤–Ķ—ā–Ĺ–ł —ā–ĺ—á–ļ–ł –ĺ—ā —Ą–ł–≥—É—Ä–ł—ā–Ķ –Ķ –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ–ĺ –Ĺ–Ķ–ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ–Ĺ–ĺ —á–ł—Ā–Ľ–ĺ, –Ĺ–į—Ä–Ķ—á–Ķ–Ĺ–ĺ –ļ–ĺ–Ķ—Ą–ł—Ü–ł–Ķ–Ĺ—ā –Ĺ–į –Ņ–ĺ–ī–ĺ–Ī–ł–Ķ. –Ę–Ķ—Ä–ľ–ł–Ĺ—ä—ā –Ķ –Ņ—Ä–ł–Ľ–ĺ–∂–ł–ľ –Ĺ–Ķ —Ā–į–ľ–ĺ –∑–į —Ä–į–≤–Ĺ–ł–Ĺ–Ĺ–ł —Ą–ł–≥—É—Ä–ł, –Ĺ–ĺ –ł –∑–į —ā–Ķ–Ľ–į –ĺ—ā —ā—Ä–ł–ł–∑–ľ–Ķ—Ä–Ĺ–ĺ—ā–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ.
–í —Ā–ł–Ľ–į —Ā–į —Ā–Ľ–Ķ–ī–Ĺ–ł—ā–Ķ —ā–≤—ä—Ä–ī–Ķ–Ĺ–ł—Ź:
- –ü–ĺ–ī–ĺ–Ī–ł–Ķ—ā–ĺ –∑–į–Ņ–į–∑–≤–į —Ä–į–≤–Ĺ–ł —ä–≥–Ľ–ł—ā–Ķ –ľ–Ķ–∂–ī—É —Ā—ä–ĺ—ā–≤–Ķ—ā–Ĺ–ł—ā–Ķ –Ľ–ł–Ĺ–ł–ł –Ĺ–į —Ą–ł–≥—É—Ä–ł—ā–Ķ.
- –ü–ĺ–ī–ĺ–Ī–ł–Ķ —Ā –ļ–ĺ–Ķ—Ą–ł—Ü–ł–Ķ–Ĺ—ā k = 1 —Ā–Ķ –Ĺ–į—Ä–ł—á–į –Ķ–ī–Ĺ–į–ļ–≤–ĺ—Ā—ā.
- –ě—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ—ā–ĺ –ľ–Ķ–∂–ī—É –Ņ–Ķ—Ä–ł–ľ–Ķ—ā—Ä–ł—ā–Ķ –Ĺ–į –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł—ā–Ķ —Ą–ł–≥—É—Ä–ł –Ķ —Ä–į–≤–Ĺ–ĺ –Ĺ–į –ļ–ĺ–Ķ—Ą–ł—Ü–ł–Ķ–Ĺ—ā–į –Ĺ–į –Ņ–ĺ–ī–ĺ–Ī–ł–Ķ k.
- –ě—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ—ā–ĺ –ľ–Ķ–∂–ī—É –Ľ–ł—Ü–į—ā–į –Ĺ–į –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł—ā–Ķ —Ą–ł–≥—É—Ä–ł –Ķ —Ä–į–≤–Ĺ–ĺ –Ĺ–į k2.
- –ě—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ—ā–ĺ –ľ–Ķ–∂–ī—É –ĺ–Ī–Ķ–ľ–ł—ā–Ķ –Ĺ–į –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł —ā–Ķ–Ľ–į –Ķ —Ä–į–≤–Ĺ–ĺ –Ĺ–į k3.
- –Ē–≤–Ķ —Ą–ł–≥—É—Ä–ł, –Ņ–ĺ–ĺ—ā–ī–Ķ–Ľ–Ĺ–ĺ –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł –Ĺ–į —ā—Ä–Ķ—ā–į, —Ā–į –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł –ł –Ņ–ĺ–ľ–Ķ–∂–ī—É —Ā–ł.
–ü–ĺ–ī–ĺ–Ī–Ĺ–ł—ā–Ķ —Ą–ł–≥—É—Ä–ł –Ķ –Ņ—Ä–ł–Ķ—ā–ĺ –ī–į —Ā–Ķ –ĺ–∑–Ĺ–į—á–į–≤–į—ā —Ā—ä—Ā —Ā–ł–ľ–≤–ĺ–Ľ–į ~ (—ā–ł–Ľ–ī–į), –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä: 
–ü–ĺ–ī–ĺ–Ī–Ĺ–ł —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł
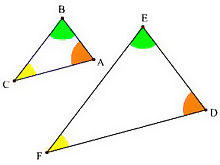 –ü–ĺ–ī–ĺ–Ī–Ĺ–ł —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł (‚ąÜCAB~‚ąÜFED)
–ü–ĺ–ī–ĺ–Ī–Ĺ–ł —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł (‚ąÜCAB~‚ąÜFED)
–ü–ĺ–ī–ĺ–Ī–Ĺ–ĺ—Ā—ā—ā–į –Ĺ–į —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł –Ķ –Ņ–ĺ–Ĺ—Ź—ā–ł–Ķ –≤ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź—ā–į. –Ē–≤–į —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ–į —Ā–į –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł, –į–ļ–ĺ –Ķ –Ĺ–į –Ľ–ł—Ü–Ķ –Ķ–ī–ł–Ĺ –ĺ—ā —Ā–Ľ–Ķ–ī–Ĺ–ł—ā–Ķ –Ņ—Ä–ł–∑–Ĺ–į—Ü–ł:
–ü—ä—Ä–≤–ł –Ņ—Ä–ł–∑–Ĺ–į–ļ –∑–į –Ņ–ĺ–ī–ĺ–Ī–ł–Ķ –Ĺ–į —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł
–ź–ļ–ĺ –ī–≤–į —ä–≥—ä–Ľ–į –Ĺ–į –Ķ–ī–ł–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ —Ā–į —Ā—ä–ĺ—ā–≤–Ķ—ā–Ĺ–ĺ —Ä–į–≤–Ĺ–ł –Ĺ–į –ī–≤–į —ä–≥—ä–Ľ–į –ĺ—ā –ī—Ä—É–≥ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ, —ā–ĺ –ī–≤–į—ā–į —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ–į —Ā–į –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł.
–í—ā–ĺ—Ä–ł –Ņ—Ä–ł–∑–Ĺ–į–ļ –∑–į –Ņ–ĺ–ī–ĺ–Ī–ł–Ķ –Ĺ–į —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł
–ź–ļ–ĺ –ī–≤–Ķ —Ā—ā—Ä–į–Ĺ–ł –Ĺ–į –Ķ–ī–ł–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ —Ā–į —Ā—ä–ĺ—ā–≤–Ķ—ā–Ĺ–ĺ –Ņ—Ä–ĺ–Ņ–ĺ—Ä—Ü–ł–ĺ–Ĺ–į–Ľ–Ĺ–ł –Ĺ–į –ī–≤–Ķ —Ā—ā—Ä–į–Ĺ–ł –ĺ—ā –ī—Ä—É–≥ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ –ł —ä–≥–Ľ–ł—ā–Ķ –ľ–Ķ–∂–ī—É —ā–Ķ–∑–ł —Ā—ā—Ä–į–Ĺ–ł —Ā–į —Ä–į–≤–Ĺ–ł, —ā–ĺ –ī–≤–į—ā–į —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ–į —Ā–į –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł.
–Ę—Ä–Ķ—ā–ł –Ņ—Ä–ł–∑–Ĺ–į–ļ –∑–į –Ņ–ĺ–ī–ĺ–Ī–ł–Ķ –Ĺ–į —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł
–ź–ļ–ĺ —Ā—ā—Ä–į–Ĺ–ł—ā–Ķ –Ĺ–į –Ķ–ī–ł–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ —Ā–į —Ā—ä–ĺ—ā–≤–Ķ—ā–Ĺ–ĺ –Ņ—Ä–ĺ–Ņ–ĺ—Ä—Ü–ł–ĺ–Ĺ–į–Ľ–Ĺ–ł –Ĺ–į —Ā—ā—Ä–į–Ĺ–ł—ā–Ķ –Ĺ–į –ī—Ä—É–≥ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ, —ā–ĺ –ī–≤–į—ā–į —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ–į —Ā–į –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł.
–ß–Ķ—ā–≤—ä—Ä—ā–ł –Ņ—Ä–ł–∑–Ĺ–į–ļ –∑–į –Ņ–ĺ–ī–ĺ–Ī–ł–Ķ –Ĺ–į —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł
–ź–ļ–ĺ –ī–≤–Ķ —Ā—ā—Ä–į–Ĺ–ł –Ĺ–į –Ķ–ī–ł–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ —Ā–į —Ā—ä–ĺ—ā–≤–Ķ—ā–Ĺ–ĺ –Ņ—Ä–ĺ–Ņ–ĺ—Ä—Ü–ł–ĺ–Ĺ–į–Ľ–Ĺ–ł –Ĺ–į –ī–≤–Ķ —Ā—ā—Ä–į–Ĺ–ł –Ĺ–į –ī—Ä—É–≥ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ –ł —ä–≥–Ľ–ł—ā–Ķ, –Ľ–Ķ–∂–į—Č–ł —Ā—Ä–Ķ—Č—É –Ņ–ĺ-–≥–ĺ–Ľ–Ķ–ľ–ł—ā–Ķ –ĺ—ā —ā–Ķ–∑–ł –ī–≤–Ķ —Ā—ā—Ä–į–Ĺ–ł, —Ā–į —Ä–į–≤–Ĺ–ł, —ā–ĺ –ī–≤–į—ā–į —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ–į —Ā–į –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł.
–ě—ā –ß–Ķ—ā–≤—ä—Ä—ā–ł—Ź –Ņ—Ä–ł–∑–Ĺ–į–ļ –∑–į –Ņ–ĺ–ī–ĺ–Ī–ł–Ķ —Ā–Ľ–Ķ–ī–≤–į –ü—Ä–ł–∑–Ĺ–į–ļ—ä—ā –∑–į –Ņ–ĺ–ī–ĺ–Ī–ł–Ķ –Ĺ–į –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–ł —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł: –ź–ļ–ĺ —Ö–ł–Ņ–ĺ—ā–Ķ–Ĺ—É–∑–į –ł –ļ–į—ā–Ķ—ā –ĺ—ā –Ķ–ī–ł–Ĺ –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ķ–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ —Ā–į —Ā—ä–ĺ—ā–≤–Ķ—ā–Ĺ–ĺ –Ņ—Ä–ĺ–Ņ–ĺ—Ä—Ü–ł–ĺ–Ĺ–į–Ľ–Ĺ–ł –Ĺ–į —Ö–ł–Ņ–ĺ—ā–Ķ–Ĺ—É–∑–į –ł –ļ–į—ā–Ķ—ā –ĺ—ā –ī—Ä—É–≥ –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ķ–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ, —ā–ĺ –ī–≤–į—ā–į —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ–į —Ā–į –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł.
–í–ł–∂—ā–Ķ —Ā—ä—Č–ĺ