William Nedham (British politician)

William Nedham (c. 1740–1806) was an Irish and British politician who sat in the House of Commons between 1774 and 1790.

Nedham was the third son of Robert Nedham MP and his wife Catherine Pitt, daughter of Robert Pitt MP of Boconnoc, Cornwall. His family had long established connections in Jamaica, but he and his father never lived there.[1] He was educated at Eton College from 1756 to 1761 and was admitted at Trinity Hall, Cambridge on 31 January 1762. He was also admitted at the Inner Temple on 2 May 1758. He was awarded MA in 1766. In 1767, he succeeded his brother and had property at Howbery Park, Oxfordshire, Edwinstone, Nottinghamshire and Symonds Place, Waresley Park, Huntingdonshire.[2]

Nedham was a member of the Parliament of Ireland for Newry from 1767 to 1776. He was returned as Member of Parliament for Winchelsea on the Nesbitt interest at a by-election on 13 August 1774, but Parliament was dissolved six weeks later. At the 1774 general election he stood at Wallingford where he was supported by Lord Abingdon, but had to withdraw after polling began.

He was High Sheriff of Oxfordshire in 1774–5. He was returned for Winchelsea again in a by-election on 3 January 1775 after Arnold Nesbitt decided to sit for Cricklade instead. In the 1780 general election Nedham was returned for Pontefract by his friend Robert Monckton-Arundell, 4th Viscount Galway. He was once again returned for Winchelsea at the 1784 general election on the Nesbitt interest. He did not stand in 1790. He appears never to have spoken in the House of Commons.[1]

Nedham died unmarried at his home in Grosvenor Square on 27 April 1806, aged 65.[2]

References

  1. ^ a b "NEDHAM, William (?1740-1806), of Howbery Park, Oxon. and Newry, co. Down". History of Parliament Online. Retrieved 9 October 2017.
  2. ^ a b "Nedham, William (NDHN762W)". A Cambridge Alumni Database. University of Cambridge.
Parliament of Great Britain
Preceded by Member of Parliament for Winchelsea
1774–1774
With: Arnold Nesbitt 		Succeeded by
Preceded by Member of Parliament for Winchelsea
1775–1780
With: Charles Wolfran Cornwall 		Succeeded by
Preceded by Member of Parliament for Winchelsea
1784–1790
With: John Nesbitt 		Succeeded by
Preceded by Member of Parliament for Pontefract
1780–1784
With: 4th Viscount Galway
Nathaniel Smith
John Smyth 		Succeeded by

Read other articles:

Gulma gelinding

Lechenaultia divaricata Gulma gelinding (Inggris: tumbleweedcode: en is deprecated ) adalah bagian struktural dari anatomi atau diaspora sejumlah spesies tumbuhan di atas tanah dimana setelah matang dan kering, ia akan terlepas dari akar atau batangnya dan menggelinding karena kekuatan angin. Pada sebagian besar spesies, gulma gelinding sebenarnya merupakan keseluruhan tanaman selain sistem akarnya, namun pada tanaman lain, buah atau bunga majemuk mungkin malah terlepas.[1] Spesies gu...

 

Kamagasaki

Kamagasaki (釜ヶ崎code: ja is deprecated ) adalah nama terdahulu untuk sebagian wilayah dari Airin-chiku (あいりん地区code: ja is deprecated ) yang menjadi nama resmi kawasan itu pada Mei 1966. Geografi Bagian dari empat kota yang berbeda — Nishinari-ku Taishi (西成区太子code: ja is deprecated ), Haginochaya (萩之茶屋code: ja is deprecated ), Sannō (山王code: ja is deprecated ), North Hanazono (花園北code: ja is deprecated ) dan Tengachaya (天下茶屋code: ja i...

 

Q'uq'umatz

Penanda lapangan bola di Mixco Viejo yang menggambarkan Q'uq'umatz yang sedang membawa Tohil di langit dengan menggunakan rahangnya Q'uq'umatz (Mayan: [qʔuː qʔuːˈmats]) (ejaan alternatif Qucumatz, Gukumatz, Gucumatz, Gugumatz, Kucumatz) adalah dewa dalam kepercayaan orang Maya K'iche' pada zaman Pascaklasik. Q'uq'umatz adalah dewa Ular Berbulu dalam kisah Popol Vuh. Ia menciptakan manusia bersama dengan dewa Tepeu. Q'uq'umatz dianggap sebanding dengan Quetzalcoatl dalam kepercayaan ...

Krum

Khan KrumPenguasa BulgariaKrum sedang memimpin pasukannyaBerkuasa803–814PendahuluKardamPenerusOmurtagKematian13 April 814WangsaDinasti Krum (kemungkinan Dulo)AnakOmurtag Budisha Khan Krum[1] (bahasa Bulgaria: Хан Крум) adalah khan Bulgaria yang berkuasa dari tahun setelah 796 tetapi sebelum 803 hingga tahun 814. Pada masa kekuasaannya, wilayah Bulgaria berlipat ganda, membentang dari tengah Donau hingga Dnieper dan dari Edrine hingga Pegunungan Tatra. Krum juga dikenang k...

 

Bandar Udara Internasional Riga

Bandar Udara Internasional RigaStarptautiskā lidosta RīgaIATA: RIXICAO: EVRAInformasiJenisPublikPemilikPemerintah LatviaMelayaniRiga, LatviaLokasiMārupe MunicipalityMaskapai penghubung airBaltic SmartLynx Airlines RAF-Avia Ryanair Ketinggian dpl11 mdplKoordinat56°55′25″N 023°58′16″E / 56.92361°N 23.97111°E / 56.92361; 23.97111Koordinat: 56°55′25″N 023°58′16″E / 56.92361°N 23.97111°E / 56.92361; 23.97111Situs...

 

Человек прямоходящий

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

Stasiun Rikuchū-Nakano

Stasiun Rikuchū-Nakano陸中中野駅Stasiun Rikuchū-Nakano pada September 2009Lokasi39-22, 3rd Jiwari, Nakano, Hirono-machi, Kunohe-gun, Iwate-ken 028-7906JepangKoordinat40°18′18″N 141°47′16″E / 40.3049°N 141.7877°E / 40.3049; 141.7877Operator JR EastJalur■ Jalur HachinoheLetak48.4 km dari HachinoheJumlah peron1 peron sampingJumlah jalur1KonstruksiJenis strukturAtas tanahInformasi lainStatusTanpa stafSitus webSitus web resmiSejarahDibuka27 Maret 1930Op...

 

United States Department of Education

U.S. federal government department For the earlier incarnation with the same name, established in 1867, see United States Office of Education. United StatesDepartment of EducationSeal of the United States Department of EducationFlag of the United States Department of EducationLyndon Baines Johnson Department of Education Building, Department HeadquartersDepartment overviewFormedOctober 17, 1979; 44 years ago (1979-10-17)Preceding agenciesDepartment of Health, Education, and ...

 

Edward Mogg

Mogg's Handbook for Railway Travellers, 1840 Edward Mogg was a publisher in London in the 19th century.[1] He issued maps and travel guides to London and other localities in England and Wales.[2] Mogg's publications appear in works of fiction such as Robert Smith Surtees' Mr. Sponge's Sporting Tour and Shirley Brooks' The Naggletons.[3][4] Further reading Survey of the high roads of England and Wales 1800s-1810s Edward Mogg (1800), Street Directory; Being a Li...

Tutupan tajuk

Tinjauan Udara tutupan tajuk Penutupan tajuk, dalam kehutanan, merupakan ukuran tutupan kanopi hutan . Penutupan tajuk dan tutupan tajuk adalah dua ukuran kanopi hutan yang sedikit berbeda dan menentukan jumlah cahaya yang dapat menembus ke lantai hutan. Penutupan tajuk, juga dikenal sebagai penutupan kanopi, adalah ukuran kanopi terpadu di atas segmen belahan langit di atas satu titik di permukaan tanah.[1] Tutupan tajuk adalah proporsi suatu tegakan yang ditutupi oleh tajuk pohon hi...

 

مايكل إمبريولي

مايكل إمبريولي معلومات شخصية الميلاد 26 مارس 1966 (العمر 58 سنة)ماونت فيرنون، الولايات المتحدة الإقامة سانتا بارباراالجانب الغربي الشمالي لمنهاتن  مواطنة الولايات المتحدة  العرق إيطاليون[1]  الديانة البوذية[2]  عضو في نقابة الكتاب الأمريكية الشرقية  الحي�...

 

Deng Xihou

Deng Xihou 邓锡侯Foto Deng Xihou dalam Biografi Terkini dari Orang-Orang Penting TiongkokLahir1889Meninggal1964PengabdianRepublik TiongkokPangkatJenderal Deng Xihou (Hanzi tradisional: 鄧錫侯; Hanzi sederhana: 邓锡侯; Pinyin: Dèng Xīhóu; 1889–1964) adalah seorang jenderal dan politisi asal Tiongkok. Biografi Deng lahir tahun 1889, di county Yingshan, Sichuan. Pada tahun 1906 ia masuk Sekolah Militer Sichuan, dan pada tahun 1909 lulus, kemudian dilanjutkan ke Sekolah...

Oyek

OyekSêga oyèk atau Sêgo oyèk, disajikan bersama kelapa parut dan tempe mendoan, dari eks Karesidenan BanyumasAsalWilayahJawa Tengah Jawa Timur D.I.YogyakartaNegara asalIndonesia Oyek (oyèk) adalah penganan yang dibuat dari tepung gaplek, diberi gula sedikit, kemudian dikukus, dapat dimakan bersama kelapa parut yang telah diberi garam sedikit. Oyek merupakan penganan pokok khas suku Jawa yang digunakan sebagai pengganti beras padi yang dibuat dari gaplek, setelah gaplek digiling menjadi t...

 

Italo-brasiliani

Italo-brasilianiÍtalo-brasileirosLuogo d'origine Italia Popolazione316.699 cittadini italiani ca. 25-30.000.000 oriundi LinguaPortoghese, talian ed italiano Religionecattolicesimo Distribuzione  Brasileincerto tra i 25 e i 30.000.000 Manuale Manifesto agli emigranti. Stima del numero di emigranti italiani in Brasile nel periodo 1876-1920, divisi per regione di provenienza[1][2] Un italo-brasiliano è una persona nata in Brasile con antenati italiani, o un itali...

 

A Christmas Carol; or, Past, Present, and Future

A play adaption of A Christmas Carol by Charles Dickens Playbill for Stirling's adaptation of A Christmas Carol (1844) A Christmas Carol; or, Past, Present, and Future is a play in three acts (or ‘Staves’) by Edward Stirling at the Adelphi Theatre in London on 5 February 1844.[1][2] Containing songs especially written for the show, the drama was adapted from the novella A Christmas Carol by Charles Dickens which had been published just weeks before in December 1843.[3&...

Alphonse Dain

Marie-Alphonse Dain Marie-Alphonse Dain (meglio noto come Alphonse Dain; Chavignon, 3 aprile 1896 – Parigi, 10 luglio 1964) è stato un grecista, paleografo, filologo classico, bizantinista ed esperto di Ellenismo francese. Fu una figura importante nel campo della codicologia e della paleografia greca e un pioniere nello studio moderno dei manuali militari bizantini. Indice 1 Biografia 2 Pubblicazioni selezionate 3 Note 4 Altri progetti 5 Collegamenti esterni Biografia Gli studi accademici ...

 

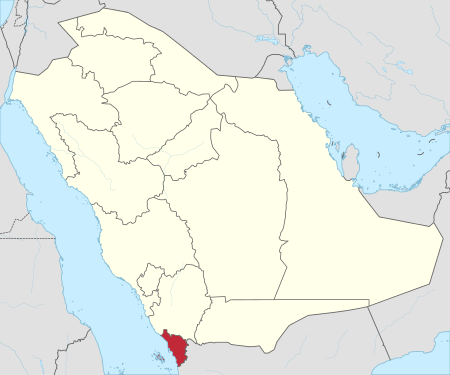
محافظة أحد المسارحة

  هذه المقالة عن محافظة أحد المسارحة. لمدينة أحد المسارحة، طالع أحد المسارحة. محافظة أحد المسارحة أحد المسارحة محافظة علم محافظة أحد المسارحةعلمOfficial seal of محافظة أحد المسارحةشعار الاسم الرسمي محافظة أحد المسارحة  صورة لخريطة محافظة أحد المسارحة نسبةً لمنطقة جازانم...

 

Nuova Zelanda ai Giochi della XXIX Olimpiade

Nuova Zelanda ai Giochi della XXIX OlimpiadePechino 2008 Codice CIONZL Comitato nazionaleComitato Olimpico della Nuova Zelanda Atleti partecipanti178 in 17 discipline Di cui uomini/donne96 - 92 PortabandieraMahé Drysdale Medagliere Posizione 25ª 3 2 4 9 Cronologia olimpica (sommario)Giochi olimpici estivi 1908* · 1912* · 1920 · 1924 · 1928 · 1932 · 1936 · 1948 · 1952 · 1956 · 1960 · 1964 · 1968 · 19...

Corporate manslaughter

Culpable conduct within a company that leads to a person's death The examples and perspective in this article may not represent a worldwide view of the subject. You may improve this article, discuss the issue on the talk page, or create a new article, as appropriate. (June 2018) (Learn how and when to remove this message) Criminal law Elements Actus reus Mens rea Causation Concurrence Scope of criminal liability Accessory Accomplice Complicity Corporate Principal Vicarious Severity of offense...

 

Multiplicative inverse

Number which when multiplied by x equals 1 Reciprocal (mathematics) redirects here. Not to be confused with Reciprocation (geometry). The reciprocal function: y = 1/x. For every x except 0, y represents its multiplicative inverse. The graph forms a rectangular hyperbola. In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is...