Unique factorization domain
|
Read other articles:

Запрос «Направленная кристаллизация» перенаправляется сюда. На эту тему нужно создать отдельную статью. Фазовые переходы первого рода на фазовой диаграмме Кристаллизация воды с образованием льда Ускоренная киносъёмка процесса роста кристалла лимонной кислоты. На вид...

Mount Rushmore National MemorialIUCN Kategori III (Monumen Alam)Gunung Rushmore dengan pahatan wajah George Washington, Thomas Jefferson, Theodore Roosevelt, dan Abraham Lincoln (dari kiri ke kanan)LetakPennington County, South DakotaKota terdekatKeystone, South DakotaLuas1.278 acres[convert: unit tak dikenal]Diizinkan3 Maret 1925Pengunjung2,431,231 (tahun 2016)[1]Pihak pengelolaNational Park ServiceSitus webMount Rushmore National Memorial Gunung Rushmore adalah gunung terkenal ...

Pour les articles homonymes, voir Barjavel. René BarjavelRené Barjavel en 1949. Photo d'identité (Sacem).BiographieNaissance 24 janvier 1911Nyons (Drôme, France)Décès 24 novembre 1985 (à 74 ans)14e arrondissement de Paris (France)Sépulture Bellecombe-TarendolNom de naissance René Henri Gustave BarjavelNationalité françaiseActivité Romancier, nouvelliste, essayiste, chroniqueur, journaliste, scénariste, dialoguistePériode d'activité 1942-1985Autres informationsConflit Seco...
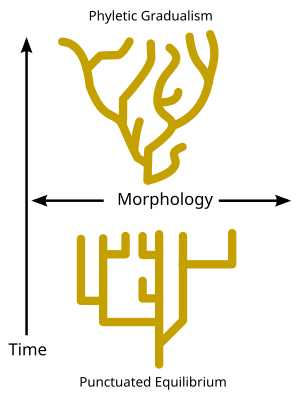
Gradualisme filetik dibandingkan dengan keseimbangan bersela (bawah). Gradualisme filetik adalah model evolusi yang menjelaskan bahwa sebagian besar spesiasi bersifat lambat, seragam, dan berangsur-angsur.[1] Seluruh spesies secara perlahan mengalami perubahan menjadi spesies yang baru. Dalam sudut pandang ini, tidak ada garis batas yang jelas antara spesies nenek moyang dengan spesies baru. Gradualisme filetik sering kali dianggap berlawanan dengan teori keseimbangan bersela, yang me...

Istilah rasul dikenal dalam Islam dan Kristen. Meski demikian, terdapat perbedaan pemahaman mengenai istilah tersebut. Dalam Islam, rasul adalah seorang Nabi dan Rasul yang mendapat wahyu dari Allah SWT, tidak hanya untuk dirinya sendiri namun wajib menyampaikan wahyu yang dia terima kepada umat, rasul terahir yang diutus oleh Allah SWT ialah Nabi Muhammad SAW membawa syariat-syariat baru yang tidak menghapuskan syariat-syariat dari rasul sebelumnya[1]. Berbeda dengan nabi biasa yang ...
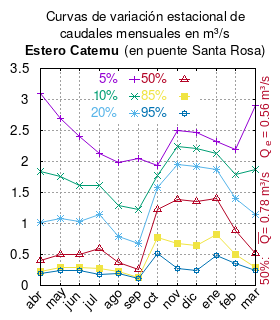
Curvas de variación estacional del estero Catemu en Santa Rosa. El diagrama muestra con la línea de triángulos rojo ocre, las medianas mensuales del caudal. Estas son los caudales mínimos que lleva el estero el 50% de los años. Se dice entonces que la probabilidad de excedencia de ese caudal es de un 50%. Las otras líneas muestran otras probabilidades de excedencia. Un caudal anual representativo del estero puede ser la media (estadística) de la serie 50%, en este caso 0,78 m³/s. Tamb...

Japanese video game publisher Entertainment Software Publishing, Inc.ESP's former headquarters in Shibuya, TokyoNative name株式会社エンターテインメント ソフトウェア パブリッシングRomanized nameKabushiki-gaisha Entāteinmento Sofutō~ea PaburisshinguCompany typeSubsidiaryIndustryVideo gamesFoundedNovember 1997; 26 years ago (1997-11)Defunct1 April 2010; 14 years ago (2010-04-01)FateMerged with D3 PublisherHeadquartersShibuya, ...

Basilika Dikandung Tanpa NodaBasilika Minor Dikandung Tanpa Nodabahasa Polandia: Bazylika na Świętej GórzeBasilika Dikandung Tanpa NodaLokasiŚwięta GóraNegara PolandiaDenominasiGereja Katolik RomaArsitekturStatusBasilika minorStatus fungsionalAktif Basilika Dikandung Tanpa Noda (bahasa Polandia: Bazylika na Świętej Górze) adalah sebuah gereja basilika minor Katolik yang terletak di Święta Góra, Polandia. Basilika ini ditetapkan statusnya pada 1970 dan didedikasikan ke...

Pour les articles homonymes, voir Grand Prix des Nations. Grand Prix moto d'Italie Dani Pedrosa, Scott Redding et Maverick Viñales au Grand Prix moto d'Italie 2016Généralités Sport Vitesse moto Création 1949 Autre(s) nom(s) Grand Prix des Nations Éditions 74 (en 2023) Catégorie Championnats du monde de vitesse moto Site(s) Mugello Circuit (1976, 1978, 1985, 1992, 1994–2019, 2021–présent) Misano Circuit (1980, 1982, 1984, 1989–1991, 1993) Imola Circuit (1969, 1972, 1974–19...

Questa voce sull'argomento calciatori tedeschi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Phil Neumann Nazionalità Germania Altezza 178 cm Peso 74 kg Calcio Ruolo Difensore Squadra Hannover 96 Carriera Giovanili Schalke 04 Squadre di club1 2016-2017 Schalke 04 II15 (1)2017-2019 Ingolstadt 0424 (1)2019-2022 Holstein Kiel72 (0)2022- Hannover 9624 (0) Nazionale ...

Ini adalah nama Korea; marganya adalah Kim. Kim Hye-yoonKim Hye-yoon di 2020Lahir10 November 1996 (umur 27)Seongnam, Gyeonggi, Korea Selatan[1]PendidikanUniversitas Konkuk [ko] - Film Studies[2]PekerjaanAktrisTahun aktif2013-sekarangAgenSidusHQ (2019 - sekarang)[3]Nama KoreaHangul김혜윤 Hanja金惠奫[1] Alih AksaraGim Hye-yunMcCune–ReischauerKim Hye-yun Kim Hye-yoon (lahir 10 November 1996) adalah aktris asal Korea Selatan. Ia palin...

Avetheropoda Periode Jura Tengah–Masa kini, 174–0 jtyl PreЄ Є O S D C P T J K Pg N Kemungkinan catatan Jura Awal Avetheropoda Cetakan kerangka Allosaurus fragilis, Museum Sejarah Alam San DiegoSeekor burung kiwi dan telurnya (1913)TaksonomiKerajaanAnimaliaFilumChordataKelasReptiliaOrdoSaurischiaTanpa nilaiAvetheropoda Gregory Scott Paul, 1988 Tata namaSinonim takson Neotetanurae Sereno et al., 1994 Orionides?[1] Carrano, Benson & Sampson, 2012 Subkelompok †Gasosau...

English footballer For the film director, see Thomas H. Ince. Tom Ince Ince playing for Hull City in 2014Personal informationFull name Thomas Christopher Ince[1]Date of birth (1992-01-30) 30 January 1992 (age 32)[2]Place of birth Stockport, EnglandHeight 5 ft 10 in (1.78 m)[3]Position(s) Attacking midfielder, winger, forwardTeam informationCurrent team WatfordNumber 7Youth career2008–2010 LiverpoolSenior career*Years Team Apps (Gls)2010–2011 Liv...

L'età di Cosimo de' MediciRitratto di Cosimo de' MediciPaeseItalia Anno1972 Formatominiserie TV Generestorico Puntate3 Durata250 min Lingua originaleitaliano, latino Rapporto1.33:1 CreditiRegiaRoberto Rossellini Soggettodalle opere di Niccolò Machiavelli e Francesco Guicciardini SceneggiaturaRoberto Rossellini, Marcella Mariani, Luciano Scaffa Interpreti e personaggi Marcello Di Falco: Cosimo de' Medici Virginio Gazzolo: Leon Battista Alberti Tom Felleghy: Rinaldo degli Albizzi Mario Erpich...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要擴充。 (2013年1月1日)请協助改善这篇條目,更進一步的信息可能會在討論頁或扩充请求中找到。请在擴充條目後將此模板移除。 此條目需要补充更多来源。 (2013年1月1日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的...

هذه المقالة عن المجموعة العرقية الأتراك وليس عن من يحملون جنسية الجمهورية التركية أتراكTürkler (بالتركية) التعداد الكليالتعداد 70~83 مليون نسمةمناطق الوجود المميزةالبلد القائمة ... تركياألمانياسورياالعراقبلغارياالولايات المتحدةفرنساالمملكة المتحدةهولنداالنمساأسترالي�...

Further information: British Empire in World War II Part of a series on theMilitary history ofSouth Africa Conflicts Khoikhoi–Dutch Wars Napoleonic Wars Xhosa Wars Ndwandwe–Zulu War South African Wars Anglo–Zulu War First Boer War Second Boer War First World War Second World War Korean War Border War National Defence Force Army Air Force History Navy Medical Services Special Forces Historical forces Union Defence Force South African Defence Force Lists Wars Battles Military chiefs vte ...

Taça de Portugal 2013-2014Taça de Portugal Millennium 2013-2014 Competizione Taça de Portugal Sport Calcio Edizione 74ª Date dal 1º settembre 2013al 18 maggio 2014 Luogo Portogallo Partecipanti 156 Risultati Vincitore Benfica(25º titolo) Secondo Rio Ave Statistiche Incontri disputati 167 Cronologia della competizione 2012-2013 2014-2015 Manuale La Taça de Portugal 2013-2014 è stata la 74ª edizione del torneo. È iniziata il 1º settembre 2013 e si è c...

Về những tàu chiến Brazil khác mang cùng tên, xin xem Amazonas (tàu chiến Brazil). Tàu ngầm USS Greenfish (SS-351) vào khoảng thập niên 1960 Lịch sử Hoa Kỳ Tên gọi USS GreenfishĐặt tên theo cá tuyết Murray[1]Xưởng đóng tàu Electric Boat Company, Groton, Connecticut[2]Đặt lườn 29 tháng 6, 1944 [2]Hạ thủy 21 tháng 12, 1945 [2]Người đỡ đầu bà Thomas J. DoyleNhập biên chế 7 tháng 6, 1946 [2...

Cemetery in Gibraltar Trafalgar CemeteryPanoramic view of the Trafalgar CemeteryDetailsEstablished1798LocationSouthport Ditch, Trafalgar RoadCountryGibraltarCoordinates36°08′05″N 5°21′08″W / 36.134747°N 5.352273°W / 36.134747; -5.352273Owned byGovernment of GibraltarFind a GraveTrafalgar Cemetery The Trafalgar Cemetery is a cemetery in the British Overseas Territory of Gibraltar. Formerly known as the Southport Ditch Cemetery, it occupies a small area of la...
![{\displaystyle \mathbb {Z} \left[e^{\frac {2\pi i}{n}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/838047c05bad92e0e14e4aa64f7995de3f248816)

![{\displaystyle \mathbb {Z} [{\sqrt {-5}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a37499ef27234d8a67a65932184280bb17301312)




![{\displaystyle \mathbb {Q} [{\sqrt {-d}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51b4edc0366ebe576d203c38dfa4f4d9638b14b2)
