Smoothed finite element method
|
Read other articles:
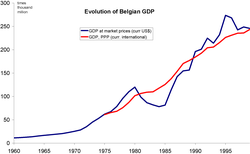
Економіка Бельгії Діловий район в районі Схарбек в БрюсселіВалюта 1 євро = 100 центівФінансовий рік календарний рікОрганізації ЄС, WTO, OECDСтатистикаВВП $508,6 млрд (2016)Зростання ВВП ▲ 1,4 % (2016)ВВП на душу населення $44 900 (2016)ВВП за секторами сільське господарство: 0,6 %, пром�...

WeserAlta sezione del Weser con ciclopistaStato Germania Länder Renania Settentrionale-Vestfalia Bassa Sassonia Assia Brema Lunghezza452 (col Werra 744) km Portata media325 m³/s Bacino idrografico46 295 km² Altitudine sorgente116,5 m s.l.m. NasceHann. Münden dall'unione di Fulda e Werra SfociaMare del Nord presso Bremerhaven Mappa del fiume Modifica dati su Wikidata · Manuale Il Weser (pronuncia tedesca /'ve:zɐ/, Visurgis in latino,[1] die Wese...

AkustichrisyeAlbum remix karya ChrisyeDirilis1996GenrePopDurasi51:39LabelMusica StudiosProduserErwin GutawaKronologi Chrisye The Best Of (1993)The Best Of1993 Akustichrisye (1996) Best Cinta (1996)Best Cinta1996 Akustichrisye adalah album remix dari penyanyi Chrisye yang dirilis pada tahun 1996. Album ini merupakan awal kerja sama Chrisye dengan Erwin Gutawa sebagai music director, dan Erwin-lah arranger yang terus menggarap musik album Chrisye sampai album terakhirnya. Album AKUSTICHRISY...

Bombing by the United States against militia groups in Syria February 2021 United States airstrike in SyriaPart of the 2019–2021 Persian Gulf crisis and the American-led intervention in the Syrian civil warLocation of Deir ez-Zor Governorate in SyriaTypeAir InterdictionLocationImam Ali military base, Abu Kamal, Deir ez-Zor Governorate, Syria[1]Planned by United StatesCommanded byJoe BidenTarget Kata'ib HezbollahKata'ib Sayyid al-ShuhadaDate25 February 2021&#...

Football clubNK Troglav 1918 LivnoFull nameNogometni klub Troglav 1918 LivnoFounded1918refounded on 17 September 2014GroundZgona, LivnoCapacity1,000 (836 seats)ChairmanDubravko PervanManagerDanijel KrivićLeagueSecond league of the FBiH(third level) Home colours Away colours NK Troglav 1918 is a football club from Livno, Bosnia and Herzegovina. It is a member of the Second League of the Federation of Bosnia and Herzegovina – group South, third level of football in the country. The club was ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Nothing Is Real but the Girl – news · newspapers · books · scholar · JSTOR (March 2017) (Learn how and when to remove this message) 1999 single by BlondieNothing Is Real but the GirlSingle by Blondiefrom the album No Exit ReleasedMay 31, 1999 (1...

American racing driver (1949–2022) NASCAR driver Michael PotterPotter in 1985Born(1949-07-04)July 4, 1949Johnson City, TennesseeDiedOctober 31, 2022(2022-10-31) (aged 73)NASCAR Cup Series career60 races run over 14 yearsBest finish36th (1992)First race1979 Southeastern 500 (Bristol)Last race1993 TranSouth 500 (Darlington) Wins Top tens Poles 0 0 0 NASCAR Xfinity Series career20 races run over 6 yearsBest finish68th (2003)First race1982 Goody's 300 (Daytona)Last race2008 Camping World R...

Questa voce o sezione sull'argomento associazioni non cita le fonti necessarie o quelle presenti sono insufficienti. Commento: Manca totalmente di fonti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Preparativi per partecipazione alla Mensur di un membro di una confraternita polacca (Korporacja Akademicka Sarmatia) contro una tedesca (Friburgo in Brisgovia, 2004) Una confraternita studentesca è un'associazione di st...

Экономика Египта Каир — центр деловой жизни страны Валюта египетский фунт Международныеорганизации ВТО Статистика ВВП $339 млрд Рост ВВП ▲ 1,8 % ВВП на душу населения $4800 ВВП по секторам сельское хозяйство: 14,5 %промышленность: 37,5 %сфера услуг: 48 % Инфляция (ИПЦ) 9 ...

Untuk nama bandara, lihat: Bandar Udara Depati Amir. Untuk nama stadion, lihat: Stadion Depati Amir. Depati Amir (lahir di Mendara, Bangka, 1805 - meninggal di Air Mata, Kota Lama, Kupang, Nusa Tenggara Timur, 28 September 1869) merupakan salah satu pahlawan nasional dari Bangka. Semangat kepahlawanannya menggema hampir di seluruh Pulau Bangka. Depati Amir aktif melawan penjajahan Belanda di Bangka yang saat itu memiliki kepentingan terhadap aktivitas tambang timah. Karena perlawanannya dinil...

1991 American television series Fishing with JohnDVD coverCreated byJohn LurieStarringJohn LurieJim JarmuschTom WaitsMatt DillonWillem DafoeDennis HopperNarrated byRobb WebbOpening themeFishing With John by John LurieCountry of originUnited StatesOriginal languageEnglishNo. of seasons1No. of episodes6ProductionExecutive producerKenji OkabeRunning time30 minutesOriginal releaseNetworkBravoIFCReleaseNovember 20 (1991-11-20) –December 25, 1991 (1991-12-25)RelatedPainting with Jo...

Artikel ini bukan mengenai Francis Dee. Frances DeeDee pada tahun 1936Lahir(1909-11-26)26 November 1909[1][2]Los Angeles, California, A.S.Meninggal6 Maret 2004(2004-03-06) (umur 94)Norwalk, Connecticut. A.S.PekerjaanAktrisTahun aktif1930–1953Suami/istriJoel McCrea (m. 1933; wafat 1990)Anak3, termasuk Jody McCrea Frances Marion Dee (26 November 1909 – 6 Maret 2004) adalah seorang aktris Amerika. Film pertamanya adalah musikal Playboy of Paris (1930)....

Species of bird This article may be too long to read and navigate comfortably. Consider splitting content into sub-articles, condensing it, or adding subheadings. Please discuss this issue on the article's talk page. (January 2024) Red-tailed hawk Red-tailed hawk call Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Aves Order: Accipitriformes Family: Accipitridae Genus: Buteo Species: B. j...

House of Hohenzollern-Sigmaringen (Romanian branch)House of Hohenzollern-RomaniaHouse of RomaniaParent houseHohenzollernCountryRomaniaFounded10 May 1866FounderCarol ICurrent headMargareta of RomaniaFinal rulerMichael ITitlesPrince (Domnitor, or Principe) (1866–1881),King (Rege) (1881–1947)Deposition30 December 1947 Former reigning dynasty of Romania Romanian royal familyCoat of arms of the Kingdom of Romania (1881-1947) HM The Custodian of the CrownHRH Prince Radu* HRH Princess Elena HRH ...

Pacific atoll and unorganized incorporated U.S. territory Place in the United StatesPalmyra AtollIncorporated territory of the United StatesUnited States Minor Outlying IslandsTerritory of Palmyra IslandPalmyra Atoll visitor access mapLocation of Palmyra Atoll in the Pacific OceanSovereign state United StatesAnnexed by the United StatesJune 14, 1900Named forU.S. trading ship PalmyraGovernmentNational Wildlife Refuge• Administered by United States Fish and Wildlife Service• ...

Style of ballroom dance This article is about the ballroom dance. For other musical styles, see Rumba. RhumbaStylistic originsSon cubano, American ballroom musicCultural originsEast Coast of the United States, early 1930sTypical instrumentsVocals, trumpet, saxophone, trombone, guitar, piano, violin, bass, maracas, congas, bongos, timbales, drumsSubgenresBallroom congaRegional scenesNew York City Rhumba, also known as ballroom rumba, is a genre of ballroom music and dance that appeared in the ...

Historic site in New South Wales, AustraliaEl Alamein Memorial FountainEl Alamein Memorial FountainLocationMacleay Street, Kings Cross, City of Sydney, New South Wales, AustraliaCoordinates33°52′22″S 151°13′30″E / 33.8729°S 151.2250°E / -33.8729; 151.2250Built1959–1961ArchitectRobert WoodwardPhill Taranto New South Wales Heritage RegisterOfficial nameEl Alamein Memorial Fountain; Fitzroy Gardens Group; Kings Cross Fountain; King's Cross FountainTypeS...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Kesatria iman adalah orang yang menempatkan iman bulat dalam diri sendiri dan dalam Allah dan dapat bertindak bebas dan independen dari duniawi. Filsuf Denmark abad ke-19 Søren Kierkegaard membahas kesatria iman dalam beberapa karya pseudonimnya, deng...

Film genre The action film is a film genre that predominantly features chase sequences, fights, shootouts, explosions, and stunt work. The specifics of what constitutes an action film has been in scholarly debate since the 1980s. While some scholars such as David Bordwell suggested they were films that favor spectacle to storytelling, others such as Goeff King stated they allow the scenes of spectacle to be attuned to story telling. Action films are often hybrid with other genres, mixing into...

International organisation for governing Broomball IFBA redirects here. For another use, see Federal Institute of Bahia. International Federation of Broomball AssociationsInternational Federation of Broomball Associations logoAbbreviationIFBAFormation1998; 26 years ago (1998)TypeSports federationLegal statusGoverning body of BroomballPurposeSport governanceHeadquartersCanadaRegion served WorldwideOfficial languages EnglishWebsiteIFBA The International Federation of Broomball...