Scott–Potter set theory
|
Read other articles:

Bagian dari monumen pada Condottieri Giovanni dalle Bande Nere. Kekerasan seksual pada masa perang adalah pemerkosaan atau bentuk-bentuk kekerasan seksual yang dilakukan oleh pejuang selama konflik bersenjata atau perang atau pendudukan militer yang sering kali dianggap sebagai rampasan perang; tapi terkadang, terutamanya dalam konflik etnis, fenomena tersebut memiliki motif sosiologis yang lebih luas. kekerasan seksual pada masa perang juga mungkin termasuk pemerkosaan beramai-ramai dan peme...

African Union-United Nations Hybrid operation in Darfur DataNama singkatUNAMID Tipepeacekeeping mission (en) MenggantikanAfrican Union Mission in Sudan (en) Sejak31 Juli 2007Tanggal pembubaran31 Desember 2020 Situs webunamid.unmissions.org Sunting di Wikidata • L • B Operasi Gabungan PBB-Uni Afrika di Darfur (Inggris: African Union-United Nations Hybrid Operation in Darfurcode: en is deprecated ; UNAMID) adalah sebuah misi penjaga perdamaian yang diselenggarakan secara bersama-s...

Desa BajangDesaBukit brukoh bajang pakong pamekasanNegara IndonesiaProvinsiJawa TimurKabupatenPamekasanKecamatanPakongKode pos69352Kode Kemendagri35.28.09.2005 Luas156.595Jumlah penduduk1.764 jiwaKepadatan- Desa Bajang adalah desa yang terletak di Kecamatan Pakong Kabupaten Pamekasan. Di desa Bajang terdapat objek wisata yaitu Bukit Brukoh yang memiliki pemandangan alam yang masih indah dan asri. Luas wilayah dari Desa Bajang adalah 156.595 . Geografis Secara geografis desa Bajang terlet...

Al-MasfaLingkunganNegaraArab SaudiProvinsiProvinsi MakkahPemerintahan • Wali kotaHani Abu Ras[1] • Gubernur kotaMish'al Al-SaudKetinggian12 m (39 ft)Zona waktuUTC+3 (AST) • Musim panas (DST)ASTKode pos(5 kode digit dimulai dari 23; e.g. 23434)Kode area telepon+966-12Situs webwww.jeddah.gov.sa/english/index.php Al-Masfa adalah sebuah permukiman padat penduduk di kota Jeddah di Provinsi Makkah, tepatnya di sebelah barat Arab Saudi.[3]...

Corregimiento in Herrera, PanamaRincón HondoCorregimientoCountry PanamaProvinceHerreraDistrictPeséArea[1] • Land29 km2 (11 sq mi)Population (2010)[1] • Total1,416 • Density48.9/km2 (127/sq mi) Population density calculated based on land area.Time zoneUTC−5 (EST) Rincón Hondo is a corregimiento in Pesé District, Herrera Province, Panama with a population of 1,416 as of 2010.[1] Its population a...

Former UK government ministry For other uses, see Colonial Office (disambiguation). The Whitehall headquarters of the Foreign, India, Home, and Colonial Offices in 1866. It was at that time occupied by all four government departments; now it serves just the Foreign, Commonwealth and Development Office. The Colonial Office was a government department of the Kingdom of Great Britain and later of the United Kingdom, first created in 1768 from the Southern Department to deal with colonial affairs...

School in Houston, Texas, United States Douglas MacArthur High SchoolAddress4400 Aldine Mail Rt. Houston, TX 77093Coordinates29°54′05″N 95°19′44″W / 29.9015°N 95.3288°W / 29.9015; -95.3288InformationEstablished1965School districtAldine Independent School DistrictPrincipalShauna ShowersStaff170.92 (FTE)[2]Grades9-12Enrollment2,826 (2018-19)[1]Student to teacher ratio17.46[2]Color(s)Silver, Red and White Team nameGe...

Most popular songs of the year in Australia 1997 Triple J Hottest 100Album artwork for the CD compilationCountdown detailsDate of countdown26 January 1998Countdown highlightsWinning songThe Whitlams(No Aphrodisiac)Most entriesThe Whitlams (2)The Verve (2)Radiohead (2)Jebediah (2)Silverchair (2)The Living End (2)Faith No More (2)Grinspoon (2)Ween (2)The Bloodhound Gang (2)Arkarna (2)Everclear (2)Chronology ← Previous1996 Next →1998 All Time The 1997 Triple J Hottest 100, was a co...

Европейская сардина Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеГруппа:Костные рыбыКласс:Лучепёрые рыбыПодкласс:Новопёры...

Artikel biografi ini ditulis menyerupai resume atau daftar riwayat hidup (Curriculum Vitae). Tolong bantu perbaiki agar netral dan ensiklopedis.Ramadhani Kirana Putra Wakil Wali Kota Solok ke-5PetahanaMulai menjabat 26 Februari 2021PresidenJoko WidodoGubernurMahyeldi AnsharullahWali KotaZul ElfianPendahuluIrzal IlyasPenggantiPetahana Informasi pribadiLahir8 Juli 1987 (umur 36)Solok, Sumatera BaratPartai politikNasDemAfiliasi politiklainnyaGolkar (2013–2020)Suami/istriNanda Dona...
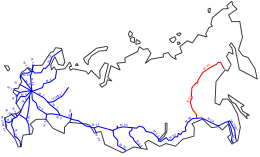
Strada A360 LenaLocalizzazioneStato Russia DatiClassificazionestrada federale InizioJakutsk FineSkovorodino Lunghezza1235 km Percorso Manuale Strada statale A360 «Lena» La strada federale A360 «Lena» (in russo Федеральная автомобильная дорога А360 «Лена»?) è una strada federale nella Repubblica della Sacha-Jacuzia che collega la città di Jakutsk con il corridoio della ferrovia Transiberiana vicino a Skovorodino, nell'Oblast' dell'Amur (Circ...

Feeding behaviour Look up paedophagy in Wiktionary, the free dictionary. The orange chromide, (Pseudetroplus maculatus) will feed on eggs Paedophagy (literally meaning the consumption of children) in its general form is the feeding behaviour of fish or other animals whose diet is partially, or primarily the eggs or larvae of other animals. However, P. H. Greenwood, who was the first to describe paedophagia, defines it to be a feeding behaviour evolved among cichlid fishes.[1][2 ...

قوات الأمن الوطني الفلسطيني الدولة دولة فلسطين الإنشاء 1994 جزء من الأجهزة الأمنية الفلسطينية المقر الرئيسي رام الله مناطق العمليات الضفة الغربية الاشتباكات هبة النفق الانتفاضة الفلسطينية الثانية الموقع الرسمي الموقع الرسمي القادة القائد الحالي اللو...

Volvode of Wallachia This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (November 2009) (Learn how and when to remove this message) Radu MihneaPrince of Wallachia(1st reign)ReignNovember 1601 – March 1602PredecessorSimion MovilăSuccessorSimion MovilăPrince of Wallachia(2nd reign)ReignApril – May 1611PredecessorGabriel BáthorySuccessorRadu ȘerbanPrince of ...

History of conservatism in the United States This article is part of a series onConservatismin the United States Schools Compassionate Fiscal Fusion Libertarian Moderate Movement Neo Paleo Progressive Social Traditionalist Principles American exceptionalism Anti-communism Christian nationalism Classical liberalism Constitutionalism Familialism Family values Federalism States' rights Judeo-Christian values Individualism Law and order Limited government Militarism Moral absolutism Natural law P...

この記事は英語版の対応するページを翻訳することにより充実させることができます。(2024年5月)翻訳前に重要な指示を読むには右にある[表示]をクリックしてください。 英語版記事を日本語へ機械翻訳したバージョン(Google翻訳)。 万が一翻訳の手がかりとして機械翻訳を用いた場合、翻訳者は必ず翻訳元原文を参照して機械翻訳の誤りを訂正し、正確な翻訳にし�...

青州府在山东省的位置(1820年) 青州府,明清时設置的府。 元朝时为益都路,属山东东西道宣慰司。至正二十七年(1367年),朱元璋政权改益都路为青州府。下领一州,十三县:益都县、临淄县、博兴县、高苑县、乐安县、寿光县、昌乐县、临朐县、安丘县、诸城县、蒙阴县、莒州(沂水县、日照县)[1]。 清代初期,領安東衞,州一,縣十三。雍正中,莒直隸,割�...

兄貴 Big Brother ポスター監督 アラン・ドワン製作 ジェシー・L・ラスキーアドルフ・ズコール出演者 トム・ムーアエディス・ロバーツレイモンド・ハットンジョー・キングミッキー・ベネットチャールズ・ヘンダーソンポール・パンサー製作会社 フェイマス・プレイヤーズ=ラスキー(英語版)配給 パラマウント映画公開 1923年12月23日 (1923-12-23) 上映時間 70分製作国...

This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Roberts v. United States Jaycees – news · newspapers · books · scholar · JSTOR (November 2019) (Learn how and when to remove this message) 1984 United States Supreme Court caseRoberts v. United States JayceesSupreme Court of the United StatesArgued April 18, 1984Decided July 3, 1984Full case nameKathryn R...

Trönö sockenSocken Trönö gamla kyrkaLandSverigeLandskapHälsinglandKommunSöderhamns kommunBildadmedeltidenArea176 kvadratkilometerUpphov tillTrönö landskommunTrönö församlingMotsvararTrönö distriktTingslagSydöstra Hälsinglands domsagas tingslag (1948-01-01–)Ala tingslag (1907-01-01–1947-12-31)Norrala tingslag (–1906-12-31)Karta Trönö sockens läge i Gävleborgs län. Trönö sockens läge i Gävleborgs län.Koordinater61°23′03″N 16°52′51″Ö / 61...