Schläfli double six
|
Read other articles:

Isotop utama oksigen Isotop Peluruhan kelimpahan waktu paruh (t1/2) mode produk 16O [99,738%, 99,776%] stabil 17O [0,0367%, 0,0400%] stabil 18O [0,187%, 0,222%] stabil Berat atom standar Ar°(O)[15,99903, 15,99977]15,999±0,001 (diringkas)[1]lihatbicarasunting Oksigen (8O) memiliki tiga isotop stabil: 16O, 17O, dan 18O. Isotop radioaktif oksigen mulai dari 11O hingga 28O juga telah dikarakterisasi, semuanya berumur pendek. Radioisotop yan...

Battambangបាត់ដំបង Statistik Luas: 11,702 km² Penduduk: 793,129 (1998) Kepadatan: 67.7 penduduk/km² ISO 3166-2: KH-2 Peta Battambang (atau Batdambang) adalah sebuah provinsi di Kamboja. Terletak di barat laut dari wilayah Kamboja dan beribu kota di Battambang. Nama Battambang diambil dari legenda Tongkat Raja Kranhoung (Preah Bat Dambang Kranhoung). Provinsi ini dibagi ke dalam 13 distrik (srok): 0201 Banan 0202 Thma Koul 0203 Bat Dambang 0204 Bavel 0205 Ek Phnom 02...

Ilustrasi dari Dinasti Qing akan Zhang Fei Zhang Fei (Hanzi:張飛 ;Pinyin: Zhāng Fēi; Han Kuno: *C.traŋ *Cə.pə[r] (Baxter-Sagart); *taŋ *pɯl (Zhengzhang Shangfang)), bernama lengkap Zhang Yide (張益德 / 张翼德), saudara angkat termuda dari Liu Bei dan Guan Yu dan seorang panglima perang terkenal pada Zaman Tiga Negara. Dalam novel Kisah Tiga Negara karangan Luo Guan Zhong. Di kalangan Tionghoa Indonesia, ia dikenal juga dengan nama Tio Hoei. Biografi Sejarah Zhang Fei (Zhan...

Election for the governorship of the U.S. state of Tennessee See also: 2018 United States gubernatorial elections 2018 United States Virgin Islands gubernatorial election ← 2014 November 6, 2018 (first round)November 20, 2018 (runoff) 2022 → Registered51,095Turnout26,346 (runoff: 23,032) Candidate Albert Bryan Kenneth Mapp Party Democratic Independent Running mate Tregenza Roach Osbert Potter Popular vote 9,711 general 12,677 runoff 8,529 general 10,288 ...
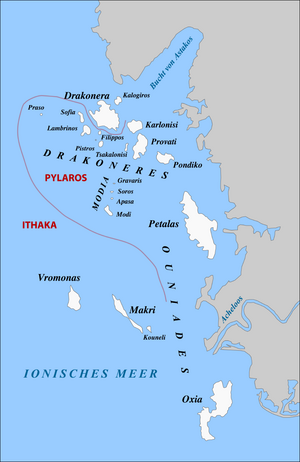
Group of islands in the Ionian Sea The Echinades The Echinades (/ɪˈkɪnədiːz/; Greek: αἱ Ἐχινάδες νῆσοι per Herodotus, Thucydides, and Strabo, per Homer Echinae (αἱ Ἐχῖναι νῆσοι, Italian: Curzolari) are a group of islands in the Ionian Sea, off the coast of Acarnania, Greece. The archipelago is commonly subdivided into three groups: the Drakoneres in the north, the Modia in the middle and the Ouniades in the south. Administratively, the Echinades form pa...

The Broadway BubbleIklanSutradaraGeorge L. SargentDitulis olehGraham BakerHarry DittmarBerdasarkanCerpen The Broadway Bubble:Leigh Gordon GiltnerPemeranCorinne GriffithSinematograferRobert StewartCharles J. DavisDistributorVitagraph Company of AmericaTanggal rilis Oktober 1920 (1920-10) Durasi5 rolNegaraAmerika SerikatBahasaBisu (intertitel Inggris) The Broadway Bubble adalah sebuah film drama bisu Amerika Serikat tahun 1920 yang hilang[1] garapan George L. Sargent dan menampilka...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...
周處除三害The Pig, The Snake and The Pigeon正式版海報基本资料导演黃精甫监制李烈黃江豐動作指導洪昰顥编剧黃精甫主演阮經天袁富華陳以文王淨李李仁謝瓊煖配乐盧律銘林孝親林思妤保卜摄影王金城剪辑黃精甫林雍益制片商一種態度電影股份有限公司片长134分鐘产地 臺灣语言國語粵語台語上映及发行上映日期 2023年10月6日 (2023-10-06)(台灣) 2023年11月2日 (2023-11-02)(香�...

1350-1905 state in Southeast Asia Sultanate of Buayanكسولتانن نو بواينKasultanan nu Buayanc.1350–1905 Seal of Datu Uto (1875–1899) The territorial map of the Sultanate of Buayan in 1875 during the reign of Datu Utto.CapitalBuayan (1350–c.1860)Bacat (c.1860–1872; 1875–1899)Kudarangan (1872–1875)Tinungkup (1899–1905)Common languagesMaguindanaon, Iranun, Teduray, Manobo languages and BlaanReligion IslamDemonym(s)BuayanenGovernmentAbsolute monarchySultan/Datu/Raj...

حصار رودس جزء من الحروب العثمانية في أوروبا التاريخ وسيط property غير متوفر. بداية 1480 نهاية 1480 الموقع رودس 36°10′00″N 28°00′00″E / 36.166666666667°N 28°E / 36.166666666667; 28 تعديل مصدري - تعديل في عام 1480 صمدت حامية فرسان الإسبتارية الصغيرة في جزيرة رودس ضد هجو...

2021 National Wrestling Alliance pay-per-view event NWA When Our Shadows FallPromotional posterPromotionNational Wrestling AllianceDateJune 6, 2021CityAtlanta, GeorgiaVenueGPB StudiosPay-per-view chronology ← PreviousBack For The Attack Next →EmPowerrr When Our Shadows Fall was a professional wrestling pay-per-view event promoted by the National Wrestling Alliance (NWA). It took take place on June 6, 2021, in Atlanta, Georgia at GPB Studios, and aired exclusively on FITE TV.[...

Constitutional body of the Congress of the Philippines For the Indian government committee, see Appointments Committee of the Cabinet. Commission on Appointments19th CongressHistoryFounded1935 (1935)1987 (1987) (reestablishment)New session startedJuly 25, 2022 (2022-07-25)LeadershipChairmanFrancis Escudero, NPC since May 20, 2024 Vice ChairmanRamon Guico Jr., Lakas since August 23, 2022 Majority LeaderLuis Raymund Villafuerte, NUP since August 23, 2022 Min...
Questa voce sull'argomento cestisti statunitensi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Tony BobbittNazionalità Stati Uniti Altezza193 cm Peso86 kg Pallacanestro RuoloGuardia Termine carriera2012 CarrieraGiovanili ?-2000Mainland High School2000-2002Southern Idaho C.C.2002-2004 Cincinnati Bearcats Squadre di club 2004-2005 L.A. Lakers2 (5)2005-2006 Scandone Avellino19 (224)...

Pour les articles homonymes, voir Meuble (homonymie). Les meubles sont l'ensemble des éléments de mobilier qui, dans un logement, un bureau, etc. sert au confort des habitants ou des utilisateurs (chaises, lits, tables…), au rangement d'objets divers (armoires, buffets, commodes, bibliothèques…). Les meubles de rangement, qui comportent usuellement des étagères, des tiroirs ou des portes, servent à ranger de petits objets tels que les vêtements, outils et ustensiles, livres ou enc...

Ethnic group Ethnic group Tamil MauritiansTotal population12.4% of Indo-Mauritians - 6% of the total population (2011 census)Regions with significant populationsThroughout the country, in Indo-Mauritian majority zonesLanguagesTamil, Mauritian Creole, Bhojpuri, Hindi, English, FrenchReligionHinduism (As per Mauritian conventions, converts to Christianity join the broader Creole population)Related ethnic groupsTamil diaspora, Telugu people, Tamil South Africans, Tamil Reunionaise, Tamil Malaysi...

Skyscraper in Manhattan, New York CitySpireSeen in June 2005Alternative namesCitySpire CenterGeneral informationLocation150–156 West 56th StreetCoordinates40°45′51″N 73°58′47″W / 40.76417°N 73.97972°W / 40.76417; -73.97972Construction started1985Topped-outJune 1987Completed1990OwnerTishman SpeyerHeightAntenna spire814 ft (248 m)Top floor75Technical detailsFloor count73Floor area830,000 sq ft (77,110 m2)Lifts/elevators10Design and...

Amusement park in Seaside Heights, New Jersey Casino PierCasino Pier as seen from the south prior to Hurricane SandyLocationSeaside Heights, New Jersey, United StatesCoordinates39°56′33″N 74°04′09″W / 39.9426°N 74.0692°W / 39.9426; -74.0692Opened1932OwnerStorino familySloganRebuilding Family MemoriesOperating seasonyear-roundAttractionsTotal31Roller coasters3Water rides1Websitewww.casinopiernj.com Casino Pier is an amusement park situated on a pier, in Seas...

Roy E. DisneyDisney pada tanggal 11 Desember 2007LahirRoy Edward Disney(1930-01-10)10 Januari 1930Los Angeles, California, ASMeninggal16 Desember 2009(2009-12-16) (umur 79)Newport Beach, California, ASPekerjaanEksekutif film Eksekutif bisnisTahun aktif1954–2009Suami/istriPatricia Ann Dailey (1955–2007)Leslie DeMeuse-Disney (2008–2009) Roy Edward Disney, KCSG (10 Januari 1930 – 16 Desember 2009)[1] adalah pejabat eksekutif senior The Walt Disney Company...

雅博蒂卡图巴斯Jaboticatubas市镇雅博蒂卡图巴斯在巴西的位置坐标:19°30′50″S 43°44′42″W / 19.5139°S 43.745°W / -19.5139; -43.745国家巴西州米纳斯吉拉斯州面积 • 总计1,113.774 平方公里(430.031 平方英里)人口 • 總計15,496人 • 密度13.9人/平方公里(36人/平方英里) 雅博蒂卡图巴斯(葡萄牙语:Jaboticatubas)是巴西米纳斯吉拉斯州的...

