Quot scheme
|
Read other articles:

1985 novel by Douglas Adams Front cover of the original UK edition of The Original Hitchhiker Radio Scripts, 1985. Front cover of the US trade paperback edition with the alternate title of The Original Hitchhiker Radio Scripts, 1985. Front cover of the 25th anniversary UK trade paperback edition of The Hitchhiker's Guide to the Galaxy: The Original Radio Scripts, 2003. The Hitchhiker's Guide to the Galaxy: The Original Radio Scripts is a book, published in 1985, containing the scripts for the...

Kota DamansaraKota Damansara pada tahun 2021.Negara MalaysiaNegeri SelangorDistrikPetaling Kota Damansara (Tulisan Jawi: كوتا دامنسارا; Hanzi: 哥打白沙罗) adalah sebuah kota di Distrik Petaling, Selangor, Malaysia. Nama lain bagi Kota Damansara adalah PJU 5 (Petaling Jaya Utara 5). Kota ini mempunyai luas sekitar 1.600 hektare (3.953,7 ekar).[1] Geografis Kawasan kota ini berdekatan dengan Sungai Buloh, Subang, Shah Alam, Kepong, Mutiara Damansara, Kampu...

Charles Whitney GilmoreCharles W. Gilmore pada 1924Lahir11 Maret 1874Meninggal27 September 1945 (1945-09-28) (aged Kesalahan ekspresi: Operator < tak terduga)KebangsaanAmerikaPekerjaanPaleontologTempat kerjaUnited States National MuseumGelarCurator of Vertebrate Paleontology Charles Whitney Gilmore (11 Maret 1874 – 27 September 1945) adalah seorang paleontolog asal Amerika Serikat yang dikenal pada awal abad ke-20 akan hasil kerjanya dalam bidang fosil-fosil vert...

Chronologies Données clés 1636 1637 1638 1639 1640 1641 1642Décennies :1600 1610 1620 1630 1640 1650 1660Siècles :XVe XVIe XVIIe XVIIIe XIXeMillénaires :-Ier Ier IIe IIIe Chronologies thématiques Art Architecture, Arts plastiques (Dessin, Gravure, Peinture et Sculpture), Littérature, Musique classique et Théâtre Ingénierie (), Architecture et () Politique Droit Religion (,) Science Santé et ...
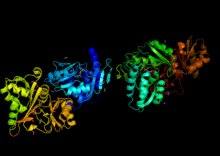
Chemical compound Not to be confused with Riboflavin-5'-phosphate. Ribose 5-phosphate Names IUPAC name 5-O-Phosphono-D-ribose Other names Ribose 5-phosphate Identifiers CAS Number 4300-28-1 Y 3D model (JSmol) Interactive image ChEBI CHEBI:58273 Y ChemSpider 70368 N ECHA InfoCard 100.022.101 MeSH ribose-5-phosphate PubChem CID 77982 UNII 4B2428FLTO Y CompTox Dashboard (EPA) DTXSID10897600 InChI InChI=1S/C5H11O8P/c6-1-3(7)5(9)4(8)2-13-14(10,11)12/h1,3-5,7-9H,2H2,(H2,10,11,12...
Olcenengo commune di Italia Tempat Negara berdaulatItaliaRegion di ItaliaPiedmontProvinsi di ItaliaProvinsi Vercelli NegaraItalia Ibu kotaOlcenengo PendudukTotal793 (2023 )GeografiLuas wilayah16,5 km² [convert: unit tak dikenal]Ketinggian149 m Berbatasan denganCasanova Elvo Collobiano San Germano Vercellese Caresanablot Quinto Vercellese Vercelli SejarahSanto pelindungCyricus and Julitta (en) Informasi tambahanKode pos13047 Zona waktuUTC+1 UTC+2 Kode telepon0161 ID ISTAT002088 Kod...

Pour les articles homonymes, voir Véronique. VéroniqueBiographieNaissance Caesarea Philippi (en)Décès Soulac-sur-MerAutres informationsÉtape de canonisation SainteFête July 9 (d), 4 févriermodifier - modifier le code - modifier Wikidata Sainte Véronique et les saintes (Hôtel Dieu à Cluny). Sixième station du chemin de croix : Véronique et Jésus. Véronique, Véronne[1] ou Bérénice est un personnage de l'époque néotestamentaire, dont l'histoire se répand entre les VIIe&...

Narrow beam of electromagnetic radiation or charged particles A pencil-beam radar A pencil-beam radar In optics, a pencil or pencil of rays is a geometric construct used to describe a beam or portion of a beam of electromagnetic radiation or charged particles, typically in the form of a narrow beam (conical or cylindrical). Antennas which strongly bundle in azimuth and elevation are often described as pencil-beam antennas. For example, a phased array antenna can send out a beam that is extrem...

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...

City in Ohio, United StatesFindlay, OhioCityDowntown FindlayNickname(s): Flag City, USAInteractive map of FindlayFindlayShow map of OhioFindlayShow map of the United StatesCoordinates: 41°02′34″N 83°38′32″W / 41.04278°N 83.64222°W / 41.04278; -83.64222CountryUnited StatesStateOhioCountyHancockArea[1] • Total19.74 sq mi (51.21 km2) • Land19.64 sq mi (50.87 km2) • Water0.13 s...

For other uses, see Hill station. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Hill town – news · newspapers · books · scholar · JSTOR (May 2010) (Learn how and when to r...
Classic Cinema redirects here. for others of the same name, see Classic Cinemas (a US chain) and Classic Cinemas, Melbourne. Historic site in Queensland, AustraliaTriumph CinemaFront of building, 2015Location963 Stanley Street, East Brisbane, City of Brisbane, Queensland, AustraliaCoordinates27°29′18″S 153°02′48″E / 27.4884°S 153.0466°E / -27.4884; 153.0466Design period1919–1930s (interwar period)Built1927ArchitectArthur RobsonArchitectural style(s)Medite...

Aspect of 2003–2011 Iraq War Siege of Sadr CityPart of the Iraq War, the Iraqi Civil War, and the Battle of Baghdad (2006–2008)Two US Army soldiers during a patrol through Sadr City in February 2006DateApril 4, 2004 – May 11, 2008(4 years, 1 month and 1 week)LocationSadr City, IraqResult Ceasefire agreement signed Iraqi government forces allowed to enter and patrol Sadr City[2] End of the Iraqi Civil WarBelligerents United States Iraq United Kingdom[1]...

Series of professional snooker tournaments The current Triple Crown logo since January 2024 (left) and previous logo (right). The Triple Crown in professional snooker refers to winning the sport's three longest-running and most prestigious tournaments: the World Snooker Championship (first held in 1927 and staged as a knockout tournament continuously since 1969), the invitational Masters (held annually since 1975), and the UK Championship (held annually since 1977). In January 2020, the three...
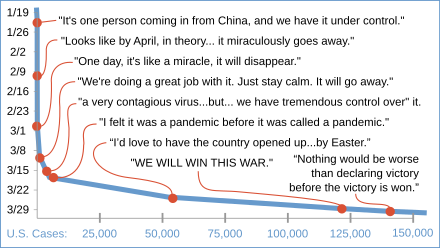
Aspect of 2020 viral outbreak This article may be too long to read and navigate comfortably. Consider splitting content into sub-articles, condensing it, or adding subheadings. Please discuss this issue on the article's talk page. (January 2022) The White House Coronavirus Task Force briefing the media. The Donald Trump administration communicated in various ways during the COVID-19 pandemic in the United States, including via social media, interviews, and press conferences with the White Hou...

Rapid transit system serving the Washington metropolitan area Washington metro redirects here. For the metropolitan area of Washington, see Washington metropolitan area. Washington MetroWashington Metro's Farragut West station in April 2018OverviewLocaleWashington metropolitan areaTransit typeRapid transitNumber of lines6Line number Number of stations98Daily ridership506,600 (weekdays, Q1 2024)[1]Annual ridership136,303,200 (2023)[2]Chief executiveRandy ClarkeHeadquarter...
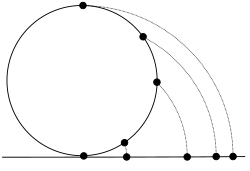
Равновеликая азимутальная проекция Ламберта с центром в 0° N 0° E и антиподом в 0° N 180° E, недалеко от Кирибати в Тихом океане. Эта точка представлена всей круговой границей карты, и океан вокруг этой точки показан вдоль всей границы. Равновеликая азимутальная проекция Ламбе...

Book by Richard Brautigan Rommel Drives on Deep into Egypt First editionAuthorRichard BrautiganCover artistEdmund SheaLanguageEnglishGenrePoetryPublisherDelacorte PressPublication date1970Publication placeUnited StatesMedia typePrint (Hardcover and Softcover)Pages85ISBN0-385-28863-8Preceded byThe Pill Versus the Springhill Mine Disaster Followed byLoading Mercury with a Pitchfork Rommel Drives on Deep into Egypt is Richard Brautigan's eighth poetry publication a...

Tim Piala Davis ArgentinaKaptenModesto VazquezPeringkat ITFPeringkat terkini4Peringkat tertinggi1 ()Penampilan pertama1921World GroupPenampilan17 (23-16)Hasil terbaik0Runner-up3 (1981, 2006 & 2008)Statistik pemainKemenangan terbanyakGuillermo Vilas (57-24)Menang terbanyak – TunggalGuillermo Vilas (45-10)Menang terbanyak – GandaGuillermo Vilas (12-14)Tim ganda terbaikGuillermo Vilas dan José Luis Clerc (7-7)Bermain terbanyakGuillermo Vilas (29)Penampilan terbanyakGuillermo Vilas (14) ...

Old town of Kraków, Poland Historic Centre of KrakówUNESCO World Heritage SiteMarket SquareLocationKraków, Kraków County, Lesser Poland Voivodeship, PolandCriteriaCultural: (iv)Reference29bisInscription1978 (2nd Session)Extensions2010Area149.65 ha (369.8 acres)Buffer zone907.35 ha (2,242.1 acres)Coordinates50°3′41″N 19°56′14″E / 50.06139°N 19.93722°E / 50.06139; 19.93722Location of Kraków Old Town in PolandShow map of PolandKraków ...


























![{\displaystyle {\mathcal {Quot}}_{{\mathcal {E}}/X/S}=\coprod _{\Phi \in \mathbb {Q} [t]}{\mathcal {Quot}}_{{\mathcal {E}}/X/S}^{\Phi ,{\mathcal {L}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f890abd582faea3b13b26c15096e25304eb3b203)






































![{\displaystyle [s]\in Q}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cf2786e0f5d8b3c950b2678cabcd9d655d7e58e)







![{\displaystyle [Z]\in {\text{Quot}}_{{\mathcal {O}}/\mathbb {P} ^{2}/{\text{Spec}}(k)}^{\lambda +1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/619ebb2770e2fb2e4775cef50709a87c612630c0)
![{\displaystyle [Z]=[a_{0}:a_{1}:a_{2}:a_{3}:a_{4}:a_{5}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd234c33c5c4c4fe1cc483b4f24e2f894b182640)

![{\displaystyle [Z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dba10cc2996611bf99b91bbb1c8c22aa504cdfe7)





















