Peter–Weyl theorem
|
Read other articles:

Pour les articles homonymes, voir Labour (homonymie), Llafur (homonymie) et Parti travailliste. Parti travailliste(en) Labour Party Logotype officiel. Présentation Chef Keir Starmer Fondation 27 février 1900 Siège 1, Brewer's GreenCité de WestminsterLondres Chef adjointe Angela Rayner Présidente Anneliese Dodds Positionnement Centre gauche à gauche[1] Idéologie Social-démocratie[2]Socialisme démocratique[3] Affiliation européenne Parti socialiste européen Affiliation international...

SMP Negeri 34 SemarangInformasiJenisNegeriAkreditasiA[1]Nomor Statistik Sekolah201036305197Nomor Pokok Sekolah Nasional20328832Kepala SekolahArbaa Insani Nuraini, S. Pd. NIP. 19710930 199802 2 003Ketua KomiteSuparnoRentang kelasVII sampai IXKurikulumKurikulum 2013 dan Kurikulum MerdekaJumlah siswa819 SiswaAlamatLokasiJl. Tlogomulyo Pedurungan, Semarang, Jawa Tengah, IndonesiaTel./Faks.(024) 6710576Koordinat6°59'57S 110°28'50ESitus webhttps://smpn34.semarangkota.g...

Pour les articles homonymes, voir Ekimov. Viatcheslav EkimovViatcheslav Ekimov (2019)InformationsSurnom EkiNom court Вячеслав ЕкимовNaissance 4 février 1966 (58 ans)VyborgNationalité russeDistinctions Liste détailléeOrdre de l'HonneurOrdre du Mérite pour la Patrie, 4e classeOrdre de l'Insigne d'honneurMaître émérite du sport de l'URSSÉquipes amateurs 1984-1989Équipe de l'URSSÉquipes professionnelles 1990-1992Panasonic-Sportlife1993Novemail-Histor-Laser Computer1...

Marble relief from Ostia Antica showing a childbirth scene Childbirth and obstetrics in classical antiquity (here meaning the ancient Greco-Roman world) were studied by the physicians of ancient Greece and Rome. Their ideas and practices during this time endured in Western medicine for centuries and many themes are seen in modern women's health. Classical gynecology and obstetrics were originally studied and taught mainly by midwives in the ancient world, but eventually scholarly physicians o...

Bandar Udara Yeosu여수공항麗水空港Yeosu GonghangYŏsu KonghangIATA: RSUICAO: RKJY RSULokasi bandar udara di Korea SelatanInformasiJenisPublicPengelolaKorean Airports CorporationMelayaniYeosuLokasiYeosu, Korea SelatanKetinggian dpl16 mdplKoordinat34°50′32.38″N 127°37′0″E / 34.8423278°N 127.61667°E / 34.8423278; 127.61667Situs webhttp://yeosu.airport.co.kr/eng/index.jspLandasan pacu Arah Panjang Permukaan m kaki 17/35 2,100 6,890 Aspal Banda...

1945 prototype multi-role combat aircraft by Henschel Hs 132 An airbrushed G. Heumann drawing of the P.132 Role Dive bomber and interceptor aircraftType of aircraft Manufacturer Henschel Flugzeugwerke AG Status Never flown Primary user Luftwaffe Produced 1945 Number built 4 prototypes[citation needed] The Henschel Hs 132 was a World War II dive bomber and interceptor aircraft of the German Luftwaffe that never saw service. The unorthodox design featured a top-mounted BMW 003 jet ...

American egg, oyster, and bacon dish Hangtown fryA hangtown burger made using a hangtown fry, a ⅓-pound chuck steak, sriracha sauce of roasted red peppers, and baby arugulaPlace of originPlacerville, CaliforniaMain ingredientsEggs, bacon and oyster Hangtown fry is a type of omelette made famous during the California Gold Rush in the 1850s. The most common version includes bacon and oysters combined with eggs, and fried together.[1] History Oakland Mayor, Visiting Newspapermen, Other...
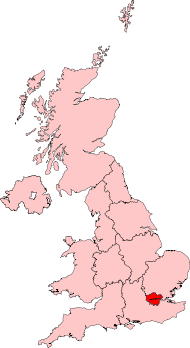
London Konstituensi Parlemen Eropa Letak di antara konstituensi 2007 Lokasi di Britania Raya Dibentuk1999 APE10 (1999 - 2004)9 (2004 - 2009)8 (2009 - sekarang) Negara anggotaBritania Raya Sumber[1][2][3] London adalah sebuah konstituensi Parlemen Eropa. Konstituensi ini memilih 8 APE menggunakan metode d'Hondt berupa perwakilan seimbang partai.[3] Batas Konstituensi ini mencakup wilayah London Raya di sebelah tenggara Britania Raya. Referensi ^ http://www.euro...

Pentecôtisme Repères historiques Fondation 1906, États-Unis Fondateur(s) Charles Fox Parham et William Joseph Seymour Fiche d'identité Courant religieux Christianisme évangélique Membres 279 millions en 2011 Localisation Monde modifier Le pentecôtisme est un mouvement chrétien évangélique, issu de réveils, lancé par les pasteurs américains Charles Fox Parham et William Joseph Seymour aux États-Unis en 1901 et 1906. Les Églises appartenant au mouvement sont appelées Égl...

Questa voce sull'argomento stagioni delle società calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: Società Sportiva Teramo Calcio. Associazione Sportiva TeramoStagione 1939-1940Sport calcio Squadra Teramo Allenatore Giovanni Battista Rebuffo Presidente Federico Cesaritti Serie C6º posto nel girone eliminatorio G 1938-1939 1940-1941 Si invita a seguire il mod...

Il mio nome è ThomasTerence Hill in una scena del filmLingua originaleitaliano Paese di produzioneItalia Anno2018 Durata96 min Generedrammatico RegiaTerence Hill SoggettoTerence Hill, Luisa Tonon SceneggiaturaTerence Hill, Luisa Tonon ProduttoreJess Hill Produttore esecutivoAnselmo Parrinello, Paolo Luvisotti Casa di produzionePaloma4 srl, Vivi Film Distribuzione in italianoLux Vide FotografiaRoberta Allegrini MontaggioLuca Benedetti Effetti specialiAlessio Pericò, Giovanni Ermes Vincenti M...

Questa voce o sezione sull'argomento centri abitati della Malaysia non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Kuala Lumpurterritorio federaleWilayah Persekutuan Kuala Lumpur Kuala Lumpur – Veduta LocalizzazioneStato Malaysia AmministrazioneMinistroMhd Amin Nordin Abdul Aziz dal 18-7-2015 TerritorioCoordinate3°08′51″N 101°41′36...

† Египтопитек Реконструкция внешнего вида египтопитека Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:Четвероно...

Temporary shelter which can be easily dismantled and which is portable For other uses, see Tent (disambiguation). A modern two-person, lightweight hiking dome tent; it is tied to rocks as there is nowhere to drive stakes on this rock shelf A tent is a shelter consisting of sheets of fabric or other material draped over, attached to a frame of poles or a supporting rope. While smaller tents may be free-standing or attached to the ground, large tents are usually anchored using guy ropes tied to...

Form of sex education Laura Bush with an AIDS orphan at a center in Zambia that promotes abstinence and faith for youth Abstinence-only sex education (also known as sexual risk avoidance education)[1] is a form of sex education that teaches not having sex outside of marriage. It often excludes other types of sexual and reproductive health education, such as birth control and safe sex. In contrast, comprehensive sex education covers the use of birth control and sexual abstinence. Evide...

This article is about the American performance art company. For their residency in Orlando, see Blue Man Group (Universal Orlando). Blue man redirects here. For Kin Platt novel, see The Blue Man. For the horror film, see The Blue Man (film). For the horse, see Blue Man (horse). Phil Stanton redirects here. For the fictional character, see Central Intelligence § Cast. This article needs additional citations for verification. Please help improve this article by adding citations to reliabl...

Indian web series For other uses, see Qubool Hai (disambiguation). Qubool Hai 2.0Directed byAnkush Mohla Glen Barretto[1]StarringKaran Singh Grover[2]Surbhi JyotiCountry of originIndiaOriginal languagesHindi, UrduNo. of seasons1No. of episodes10 (list of episodes)ProductionProducersAbhigyan Jha Mrinal Jha[1]Production locationsBelgrade,[3] Novi Sad[4][5] (Serbia)Running time25 minutesProduction companyMAJ Productions[1]Original releaseNe...

ميتال غير سوليد 4: غنز أوف ذا بتريوتسMetal Gear Solid 4: Guns of the Patriots المطور كونامي في استديوات كوجيما برودكتشن الناشر كونامي الموزع بلاي ستيشن ناو[1] المصمم هيديو كوجيما (منتج، مخرج)كينيشيرو إمايزومي (منتج)يوجي شينكاوا (مصمم الشخصيات) المخرج هيديو كوجيما الكاتب هيديو كوجي...

البرنامج الصيني لاستكشاف القمرمعلومات عامةالبلد الصين المنظم إدارة الفضاء الوطنية الصينية الهدف استكشاف القمر موقع الإطلاق Xichang Satellite Launch Center (en) تاريخ البرنامجالبداية 2003 الرحلاتأول رحلة 24 أكتوبر 2007 (شونغ'ء-1) آخر رحلة 23 نوفمبر 2020 (تشانغ آه-5) الرحلات القائمة ... تشا...

American actress (born 1994) Dakota FanningFanning in 2020BornHannah Dakota Fanning (1994-02-23) February 23, 1994 (age 30)Conyers, Georgia, U.S.Alma materNew York University (BA)OccupationActressYears active1999–presentRelativesElle Fanning (sister)Rick Arrington (grandfather)Jill Arrington (aunt) Hannah Dakota Fanning (born February 23, 1994) is an American actress.[1] She rose to prominence as a child actress at the age of seven for playing the daughter of an intel...









































