Peripheral cycle
|
Read other articles:

Untuk tokoh ini dalam sudut pandang Kristen, lihat Azura (tokoh Alkitab). AzuraNama lain Hazura Dewi Mulat Muladzura Suami/istriSyitsAnakAnwasOrang tuaAdam dan Hawa Adam (bapak)Hawa (ibu)KerabatIklima (saudari)Labuda (saudari) Qabil (saudara)Habil (saudara)Syits (saudara) Bagian dari seriIslam Rukun Iman Keesaan Allah Malaikat Kitab-kitab Allah Nabi dan Rasul Allah Hari Kiamat Qada dan Qadar Rukun Islam Syahadat Salat Zakat Puasa Haji Sumber hukum Islam al-Qur'an Sunnah (Hadis, Sirah) Ta...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Johann Wolfgang Döbereiner, seorang ahli kimia yang mengemukakan Hukum Triad Dobereiner Hukum Triad Dobereiner adalah sebuah hukum atau teori yang mengelompokkan tiga unsur kimia dengan kemiripan sifat tertentu. Pada tahun 1829, Johann Wolfgang Dober...

Gwion Edwards Gwion Edwards bermain untuk Ipswich Town di Barnet pada 21 Juli 2018Informasi pribadiNama lengkap Gwion Dafydd Rhys Edwards[1]Tanggal lahir 01 Maret 1993 (umur 31)Tempat lahir Lampeter, WalesTinggi 5 ft 9 in (1,75 m)Posisi bermain GelandangInformasi klubKlub saat ini Crawley TownNomor 7Karier junior2004–2007 Aberystwyth TownKarier senior*Tahun Tim Tampil (Gol)2011–2014 Swansea City 0 (0)2013 → St. Johnstone (pinjaman) 19 (0)2014 → Crawley Tow...

American physician and Seventh-day Adventist missionary Harry Willis MillerBornJuly 1, 1879Ludlow Falls, OhioDiedJanuary 1, 1977Riverside, CaliforniaOccupation(s)Physician, Seventh-day Adventist missionary Harry Willis Miller (July 1, 1879 – January 1, 1977) was an American physician, thyroid surgeon and Seventh-day Adventist missionary. Miller was a vegetarian and pioneer in the development of soy milk.[1] Biography Miller was born in Ludlow Falls, Ohio on July 1, 1879.[2] ...

Primeira Divisão 2022-2023Liga UNA Seguros Competizione Primeira Divisão Sport Pallavolo Edizione 77ª Organizzatore FPV Date dall'8 ottobre 2022al 7 maggio 2023 Luogo Portogallo Partecipanti 14 Risultati Vincitore Benfica(11º titolo) Secondo Fonte do Bastardo Terzo Sporting Lisbona Retrocessioni Caldas Statistiche Miglior marcatore Edson González (651) Incontri disputati 214 Cronologia della competizione 2021-22 2023-24 Manuale La Primeira Div...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Certaines informations figurant dans cet article ou cette section devraient être mieux reliées aux sources mentionnées dans les sections « Bibliographie », « Sources » ou « Liens externes » (octobre 2023). Vous pouvez améliorer la vérifiabilité en associant ces informations à des références à l'aide d'appels de notes. Saint-Denis (Seine-Saint-Denis) (93) proche banlie...

Russian composer and pianist (1872–1915) In this name that follows Eastern Slavic naming customs, the patronymic is Nikolayevich and the family name is Scriabin. Alexander ScriabinАлександр СкрябинBornAlexander Nikolayevich Scriabin6 January 1872 [O.S. 25 December 1871]Moscow, Russian EmpireDied27 April [O.S. 14 April] 1915 (aged 43)Moscow, Russian EmpireOccupationsComposerpianistWorksList of compositionsSignature Alexander Nikolayevich Scr...

Community college in Harris County, Texas, US Lone Star College–North HarrisLSC–North HarrisTypeCommunity collegeEstablished1973ChancellorMario CastilloPresidentBennie E. LambertStudents18,478[1]LocationHarris County, Texas, United StatesCampusUrban, 254 acres (1 km²)ColorsBlue and RedAffiliationsLone Star College SystemMascotHurricanesWebsitehttp://northharris.lonestar.edu Lone Star College–North Harris (formerly North Harris College, NHC) is a public community college, locate...

Disambiguazione – Koei Tecmo rimanda qui. Se stai cercando la società holding, vedi Koei Tecmo Holdings. Koei Tecmo Games Co., Ltd.Logo Sede centrale a Yokohama Stato Giappone Forma societariasocietà privata Fondazione1º aprile 2010 Sede principaleYokohama GruppoKoei Tecmo Holdings Controllate Koei Tecmo Singapore Pte, Ltd. Koei Tecmo China, Tianjin Koei Tecmo China, Beijing Koei Tecmo Software Vietnam Co., Ltd. Gust Nagano Development Group Settoreinformatico Prodotti ...

artikel ini tidak memiliki pranala ke artikel lain. Tidak ada alasan yang diberikan. Bantu kami untuk mengembangkannya dengan memberikan pranala ke artikel lain secukupnya. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Pisang amb...

Galaxy in the constellation Pegasus NGC 7814NGC 7814 by the Mount Lemmon ObservatoryObservation data (J2000 epoch)ConstellationPegasusRight ascension00h 03m 14.9s[1]Declination+16° 08′ 44″[1]Heliocentric radial velocity1050 ± 4 km/s[1]Distance40.0 ± 2.6 Mly (12.2 ± 0.8 Mpc)[2]Apparent magnitude (V)11.6[1]CharacteristicsTypeSA(S)ab[1]Apparent size (V)5.5′ × 2.3′[1]Other designationsCaldwell 43,...

Personal médico en una sala de urgencias en Luisiana, Estados Unidos. El Departamento de Emergencias (DE), a veces denominado Accidentes y Emergencia (A & E), Sala de Urgencias (SU), Emergency Ward (EW) o Departamento de Accidentes, es un hospital o departamento de atención primaria o sección de un hospital que ofrece un tratamiento inicial de pacientes con un amplio espectro de enfermedades y lesiones, algunas de las cuales pueden ser potencialmente mortales y requieren atención inme...

هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. لمعانٍ أخرى، طالع غزل (توضيح). جزء من سلسلة مقالات عنالثقافة العربية العمارة الأنماط يمني قديم نبطية أموية عباسية فاطمية مغربية مملوكية المميزات حجر أبلق بهو معمد مشرب...
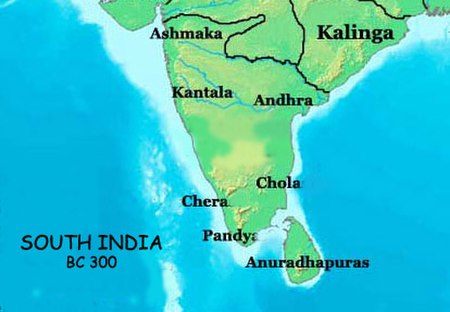
Monarchs in Ancient India For the film, see Moovendhar. A close depiction of the flags of Three Crowned Kings. Areas of influence of Cheras, Cholas and Pandyas in 300 BC Three Crowned Kings ruled Tamilakam which comprised that part of India south of the Maurya Empire in c. 250 BCE. Part of a series onHistory of Tamil Nadu Main Tamiḻakam Chronology of Tamil history List of Tamil monarchs Wootz steel Maritime contacts Sangam period Sources Three Crowned Kings Education Legal system Naming con...

豪栄道 豪太郎 場所入りする豪栄道基礎情報四股名 澤井 豪太郎→豪栄道 豪太郎本名 澤井 豪太郎愛称 ゴウタロウ、豪ちゃん、GAD[1][2]生年月日 (1986-04-06) 1986年4月6日(38歳)出身 大阪府寝屋川市身長 183cm体重 160kgBMI 47.26所属部屋 境川部屋得意技 右四つ・出し投げ・切り返し・外掛け・首投げ・右下手投げ成績現在の番付 引退最高位 東大関生涯戦歴 696勝493敗...

WatukeboDesaKantor Desa WatukeboPeta lokasi Desa WatukeboNegara IndonesiaProvinsiJawa TimurKabupatenBanyuwangiKecamatanWongsorejoKode pos68453Kode Kemendagri35.10.18.2008 Luas... km²Jumlah penduduk... jiwaKepadatan... jiwa/km² Untuk kegunaan lain, lihat Watukebo (disambiguasi). Watukebo adalah sebuah nama desa di wilayah Wongsorejo, Kabupaten Banyuwangi, Provinsi Jawa Timur, Indonesia. Pembagian wilayah Desa ini terdiri dari 4 dusun, yaitu: Dusun Krajan Dusun Maelang Dusun Pringgondani...

1935 short story by H. P. Lovecraft The Quest of IranonShort story by H. P. LovecraftThe Quest of IranonText available at WikisourceCountryUnited StatesLanguageEnglishGenre(s)FantasyPublicationPublished inGalleonPublication dateJuly/August 1935 The Quest of Iranon is a fantasy short story by American writer H. P. Lovecraft. It was written on February 28, 1921,[1] and was first published in the July/August 1935 issue of the magazine Galleon.[2] It was later reprinted in Weird ...

Tree that is decorated for Christmas For other uses, see Christmas tree (disambiguation). Christmas tree decorated with lights, stars, and glass balls Glade jul by Viggo Johansen (1891) Typical North American family decorating Christmas tree (c. 1970s) A Christmas tree is a decorated tree, usually an evergreen conifer, such as a spruce, pine or fir, or an artificial tree of similar appearance, associated with the celebration of Christmas.[1] The custom was developed in Central E...

Sally of the SawdustPosterSutradaraD. W. GriffithProduserD. W. GriffithDitulis olehForrest HalseyBerdasarkanPoppy olehDorothy DonnellyPemeranCarol DempsterW.C. FieldsAlfred LuntErville AldersonMarie ShotwellGlenn AndersSinematograferHarry Fischbeck Hal SintzenichPenyuntingRussell G. ShieldsPerusahaanproduksiParamount Pictures[1]DistributorUnited ArtistsTanggal rilis 02 Agustus 1925 (1925-08-02) Durasi104 menit[2]NegaraAmerika SerikatBahasaBisu (intertitel Inggris) Fi...

Museum in central London Bow Street Police MuseumEntrance in Martlett Court, Bow StLocation within City of WestminsterEstablishedMay 2021LocationCovent GardenLondon, WC2E 7AWCoordinates51°30′49″N 00°07′18″W / 51.51361°N 0.12167°W / 51.51361; -0.12167TypePolice museumPublic transit access Covent Garden Aldwych 11, 15, 26, 76, 172, 243, 341WebsiteOfficial website Bow Street Magistrates' Court building in 2013 The Bow Street Police Museum, opened in 2021, is b...









