Parseval's theorem
|
Read other articles:

Frank StronachLahirFranz Strohsack6 September 1932 (umur 91)Kleinsemmering, Styria, AustriaKebangsaanAustria dan KanadaPekerjaanPebisnisPemilik/peternak kuda pacuSuami/istriElfriede SallmutterAnakBelinda, AndrewPenghargaanThoroughbred horse racing awards: Sovereign Award for Outstanding Breeder(1997, 1998, 1999)Sovereign Award for Outstanding Owner(1993, 1994, 1997, 1998, 1999, 2002, 2003, 2005)Eclipse Award for Outstanding Breeder(2000, 2004, 2005, 2006, 2007, 2008)Eclipse Award for Ou...
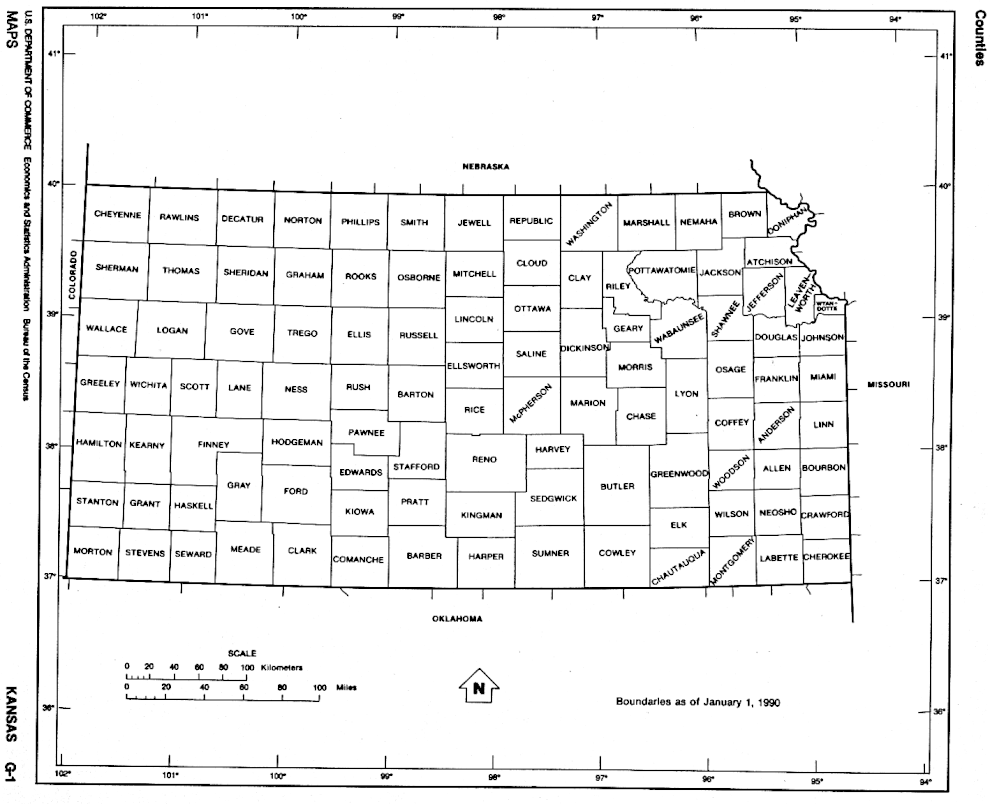
Disambiguazione – Se stai cercando altri significati, vedi Kansas (disambigua). Kansasstato federato(EN) State of Kansas (dettagli) (dettagli) LocalizzazioneStato Stati Uniti AmministrazioneCapoluogoTopeka GovernatoreLaura Kelly (D) dal 2019 Data di istituzione29 gennaio 1861 TerritorioCoordinatedel capoluogo39°03′21″N 95°41′22″W / 39.055833°N 95.689444°W39.055833; -95.689444 (Kansas)Coordinate: 39°03′21″N 95°41′22″W / þ...

Ini adalah nama Korea; marganya adalah Go. Go Min-sioleh Marie Claire Korea, 2020LahirGo Min-si15 Februari 1995 (umur 29)Seoul, Korea SelatanPekerjaanAktrisTahun aktif2017-sekarangAgenMystic EntertainmentNama KoreaHangul고민시 Hanja高旻示 Alih AksaraGo Min-siMcCune–ReischauerKo Minsi Go Min-si (Bahasa Korea: 고민시) adalah seorang aktris dan model Korea Selatan yang bernaung di bawah Mystic Story, anak perusahaan SM Entertainment. Dia memulai karier beraktingnya melalui w...

Templat:Desa=mijil,gondang legi,sambo,cinde dan grumbulijo(goligo) Gondanglegi adalah desa di kecamatan Klego, Boyolali, Jawa Tengah, Indonesia. Pranala luar (Indonesia) Keputusan Menteri Dalam Negeri Nomor 050-145 Tahun 2022 tentang Pemberian dan Pemutakhiran Kode, Data Wilayah Administrasi Pemerintahan, dan Pulau tahun 2021 (Indonesia) Peraturan Menteri Dalam Negeri Nomor 72 Tahun 2019 tentang Perubahan atas Peraturan Menteri Dalam Negeri Nomor 137 Tahun 2017 tentang Kode dan Data Wilayah A...

artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) KemlakagedeDesaNegara IndonesiaProvinsiJawa BaratKabupatenCirebonKecamatanTengahtaniKode Kemendagri32.09.35.2004 Luas... km²Jumlah penduduk....

Relief Amenemhat I, pendiri Itjtawy. Itjtawy (nama Mesir lengkap: Amenemhat-itj-tawy — Amenemhat – Perebut Dua Negeri), adalah ibu kota yang didirikan oleh firaun dinasti kedua belas Mesir Kuno Amenemhat I.[1] Kota ini terletak di Oasis Faiyum. Situs Itjtawy mungkin dipilih menjadi ibu kota karena kedekatannya dengan sumber serangan ke Mesir, agar serangan-serangan selanjutnya dapat dicegah.[2] Referensi ^ Arnold, Dorothea (1991). Amenemhat I and the Early Twelfth Dynasty ...

Часть серии статей о Холокосте Идеология и политика Расовая гигиена · Расовый антисемитизм · Нацистская расовая политика · Нюрнбергские расовые законы Шоа Лагеря смерти Белжец · Дахау · Майданек · Малый Тростенец · Маутхаузен ·&...

جزء من سلسلة مقالات سياسة بلجيكابلجيكا الدستور الدستور حقوق الإنسان السلطة التنفيذية الرئيس مجلس الوزراء السلطة التشريعية البرلمان السلطة القضائية القضاء المحكمة العليا التقسيمات الادارية أقاليم فلاندرز والونيا إقليم بروكسل العاصمة مدن الانتخابات الانتخابات الأحزاب ...

كافالا (قوله) Καβάλα Kavala الموقع الجغرافي تقسيم إداري البلد اليونان[1][2] المنطقة الإدارية مقدونيا الشرقية وتراقيا كافالا خصائص جغرافية إحداثيات 40°56′23″N 24°24′25″E / 40.93959°N 24.40687°E / 40.93959; 24.40687 المساحة 112.6 كيلومتر مربع الأرض 112.6 كم² الارتفاع 53 متر&...

Bupati LangkatLambang Kabupaten LangkatPetahanaSyah AfandinPelaksana Tugassejak 20 Januari 2022Masa jabatan5 tahun, sesudahnya dapat dipilih kembali hanya untuk 1 kaliSitus webwww.langkatkab.go.id Daftar Bupati Kabupaten Langkat dari tahun 1967 hingga sekarang:[1] No Bupati Mulai menjabat Akhir menjabat Periode Wakil Bupati Keterangan 1 T Ismail Aswhin 1967 1974 1 2 M Iscad Idris 1974 1979 2 3 R Mulyadi 1979 1984 3 4 Marzuki Erman 1984 1989 4 5 Zulfirman Siregar 1989 1994 5 6 Zul...

Exposition universelle de 1862 La machine analytique de Babbage Général Type-BIE Universelle Catégorie Expo historique Thème Industrie et arts Surface 9 hectares Inventions machine analytique Fréquentation 6.100.000 visiteurs Participants Nombre de pays 36 Localisation Pays Royaume-Uni Ville Londres Site Kensington Exhibition Road Coordonnées 51° 30′ 01,4″ nord, 0° 10′ 33,2″ ouest Chronologie Date d'ouverture 1er mai 1862 Date de clôture 1er nov...

Pour les articles homonymes, voir Armée populaire et Armée allemande. Armée populaire nationaleNationale Volksarmee Insigne de la NVA Fondation 1956 Dissolution 1990 Branches Landstreitkräfte (terre) Luftstreitkräfte (air) Volksmarine (marine) Quartier-général Berlin-Est (Strausberg) Main-d'œuvre Âges militaires 18 ans Actifs 155 319 (1989) Articles annexes Histoire Histoire militaire de l'Allemagne modifier Garde d'honneur du régiment de la garde Friedrich-Engels de la ...

Photo de L'université du Cap-Breton. L’Université du Cap-Breton (en anglais : Cape Breton University) est une université canadienne, située à Sydney, en Nouvelle-Écosse. En 2010, elle compte 3 500 étudiants. Elle ouvrit ses portes en 1951 en tant que campus de l'Université Saint-Francis-Xavier. Voir aussi (en) Site officiel v · mUniversités canadiennes Yukon Yukon Colombie-Britannique Colombie-Britannique Okanagan Northern British Columbia Royal Roads Simon Fra...

此條目需要补充更多来源。 (2021年7月4日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:美国众议院 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 美國眾議院 United States House of Representatives第118届美国国会众议院徽章 众议院旗...

العلاقات الإستونية الليبية إستونيا ليبيا إستونيا ليبيا تعديل مصدري - تعديل العلاقات الإستونية الليبية هي العلاقات الثنائية التي تجمع بين إستونيا وليبيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة إست�...

TWICE 4TH WORLD TOUR 'III', atau disebut 'III' (dibaca three), adalah tur dunia oleh girl grup Korea Selatan Twice. Menampilkan 14 konser di 3 negara di Asia dan Amerika Utara. Dimulai dengan 2 konser di Seoul pada Desember 2021 dan ditutup dengan konser encore di Amerika Serikat pada Mei 2022. TWICE 4TH WORLD TOUR 'III'Tur Dunia yang diadakan oleh TwiceTwice 4th World Tour 'III' in Seoul Official PosterAlbum terkaitEyes Wide Open Taste of Love Perfect World Formula of Love: O+T=<3Tanggal ...

Music of Cuba General topics Related articles Genres Afro Afro-Cuban jazz Bakosó Bolero (filin) Canción Chachachá Charanga Conga Contradanza (habanera) Criolla Cubatón Danzón Descarga Guajira Guaracha Hip hop Mambo Mozambique Nueva trova Pachanga Pilón Pregón Punto guajiro Rock Rumba (guaguancó, columbia, yambú, batá-rumba, guarapachangueo) Son (montuno) Songo Timba Trova Specific forms Religious music Abakuá Arará Iyesá Makuta Palo Santería Yuka Traditional music Changüí Cor...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أكتوبر 2015) كم هي سون معلومات شخصية الميلاد 28 سبتمبر 1969 (55 سنة) سول مواطنة كوريا الجنوبية الحياة العملية المدرسة الأم جامعة دانكوك المهنة ممثلة أفلام، و...

Chemical compound PapaverineClinical dataPronunciation/pəˈpævəriːn/ Trade namesPavabid, othersAHFS/Drugs.comMonographMedlinePlusa682707Pregnancycategory AU: A Routes ofadministrationOral, intravenous, intramuscular, rectal, intracavernosalATC codeA03AD01 (WHO) G04BE02 (WHO)Legal statusLegal status AU: S4 (Prescription only) US: ℞-only Pharmacokinetic dataBioavailability80%Protein binding~90%MetabolismHepaticElimination half-life1.5–2 hoursExcretionR...

Buccianonucleo abitatoBucciano – Veduta LocalizzazioneStato Italia Regione Toscana Provincia Pisa Comune San Miniato TerritorioCoordinate43°38′05.38″N 10°48′39.27″E43°38′05.38″N, 10°48′39.27″E (Bucciano) Altitudine191 m s.l.m. Abitanti52[1] (2011) Altre informazioniCod. postale56028 Prefisso0571 Fuso orarioUTC+1 Nome abitantibuccianesi CartografiaBucciano Modifica dati su Wikidata · Manuale Bucciano è una località del com...









![{\displaystyle {\begin{aligned}\sum _{n=-\infty }^{\infty }a_{n}{\overline {b_{n}}}&={\frac {1}{2\pi }}\int _{-\pi }^{\pi }{\biggl (}\sum _{n=-\infty }^{\infty }a_{n}e^{inx}{\biggr )}{\biggl (}\sum _{n=-\infty }^{\infty }{\overline {b_{n}}}e^{-inx}{\biggr )}\,\mathrm {d} x\\[6pt]&={\frac {1}{2\pi }}\int _{-\pi }^{\pi }{\Bigl (}a_{1}e^{i1x}+a_{2}e^{i2x}+\cdots {\Bigr )}{\Bigl (}{\overline {b_{1}}}e^{-i1x}+{\overline {b_{2}}}e^{-i2x}+\cdots {\Bigr )}\,\mathrm {d} x\\[6pt]&={\frac {1}{2\pi }}\int _{-\pi }^{\pi }\left(a_{1}e^{i1x}{\overline {b_{1}}}e^{-i1x}+a_{1}e^{i1x}{\overline {b_{2}}}e^{-i2x}+a_{2}e^{i2x}{\overline {b_{1}}}e^{-i1x}+a_{2}e^{i2x}{\overline {b_{2}}}e^{-i2x}+\cdots \right)\mathrm {d} x\\[6pt]&={\frac {1}{2\pi }}\int _{-\pi }^{\pi }\left(a_{1}{\overline {b_{1}}}+a_{1}{\overline {b_{2}}}e^{-ix}+a_{2}{\overline {b_{1}}}e^{ix}+a_{2}{\overline {b_{2}}}+\cdots \right)\mathrm {d} x\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfdec2af97802f389dd51d47714b85a272e014d5)

![{\displaystyle {\begin{aligned}\sum _{n=-\infty }^{\infty }a_{n}{\overline {b_{n}}}&={\frac {1}{2\pi }}\left[a_{1}{\overline {b_{1}}}x+ia_{1}{\overline {b_{2}}}e^{-ix}-ia_{2}{\overline {b_{1}}}e^{ix}+a_{2}{\overline {b_{2}}}x+\cdots \right]_{-\pi }^{+\pi }\\[6pt]&={\frac {1}{2\pi }}\left(2\pi a_{1}{\overline {b_{1}}}+0+0+2\pi a_{2}{\overline {b_{2}}}+\cdots \right)\\[6pt]&=a_{1}{\overline {b_{1}}}+a_{2}{\overline {b_{2}}}+\cdots \\[6pt]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1123fd4b262a19fa31201279c2802eeedaa8555f)





![{\displaystyle [-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)







![{\displaystyle \sum _{n=-\infty }^{\infty }{\bigl |}x[n]{\bigr |}^{2}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }{\bigl |}X_{2\pi }({\phi }){\bigr |}^{2}\mathrm {d} \phi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/136678ba72f73b10397fdffcc4b50c3bd3653fbb)



![{\displaystyle \sum _{n=0}^{N-1}{\bigl |}x[n]{\bigr |}^{2}={\frac {1}{N}}\sum _{k=0}^{N-1}{\bigl |}X[k]{\bigr |}^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d7e9127f37b8cf5b6f6996de9d29dcecf4be023)
![{\displaystyle X[k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b44d31b5739397a3a3a58892804677840e85bb2a)
![{\displaystyle x[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864cbbefbdcb55af4d9390911de1bf70167c4a3d)

![{\displaystyle {\begin{aligned}{\frac {1}{N}}\sum _{k=0}^{N-1}{\bigl |}X[k]{\bigr |}^{2}&={\frac {1}{N}}\sum _{k=0}^{N-1}X[k]\cdot X^{*}[k]={\frac {1}{N}}\sum _{k=0}^{N-1}{\Biggl (}\sum _{n=0}^{N-1}x[n]\,\exp \left(-j{\frac {2\pi }{N}}k\,n\right){\Biggr )}\,X^{*}[k]\\[5mu]&={\frac {1}{N}}\sum _{n=0}^{N-1}x[n]{\Biggl (}\sum _{k=0}^{N-1}X^{*}[k]\,\exp \left(-j{\frac {2\pi }{N}}k\,n\right){\Biggr )}={\frac {1}{N}}\sum _{n=0}^{N-1}x[n]{\bigl (}N\cdot x^{*}[n]{\bigr )}\\[5mu]&=\sum _{n=0}^{N-1}{\bigl |}x[n]{\bigr |}^{2},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2078cedb340cfed0f1524fd4940fa7d7b952719b)
