Natallia Mikhnevich
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Українські шерифи Міжнародний постерЖанр ДокументальнийРежисер Роман БондарчукПродюсер Дарина АверченкоУлдіс СекулісСценарист Дарина АверченкоОператор Роман БондарчукКомпозитор Антон БайбаковМонтаж Роман БондарчукКатерина ГорностайБорис ПетерКінокомпанія VFS Fil...

Citra gas terakresi ke lubang hitam di galaksi NGC 4261. Piringan akresi adalah struktur yang terbentuk oleh materi yang mengorbit benda yang sangat besar. Benda tersebut biasanya merupakan sebuah bintang. Gravitasi menarik materi di piringan ke benda yang diorbit. Gaya gravitasi dan friksi menekan dan meningkatkan suhu materi tersebut sehingga menghasilkan radiasi elektromagnetik. Frekuensi radiasi tersebut bergantung kepada massa objek yang dikelilingi. Piringan akresi bintang muda dan prot...

Siomay bicycle street hawker in Glodok area, Jakarta's Chinatown. This article is part of the series onIndonesian cuisineMasakan Indonesia National dishes Gado-gado Nasi goreng Rendang Satay Soto Tumpeng Regional and cultural cuisines Acehnese Arab Balinese Banjarese Batak Betawi Chinese Gorontalese Indian Indo Javanese Madurese Makassarese Malay Minahasan Minangkabau Palembangese Peranakan Sundanese Ingredients Bumbu Condiments Peanut sauce Sambal Santan Types of food Foods Dishes Noodles So...

1920s Bauhaus-influenced art movement in photography Carnival masks, or three sliced onions, by Elsa Thiemann, 1930s The Neues Sehen, also known as New Vision or Neue Optik, was a movement, not specifically restricted to photography, which was developed in the 1920s. The movement was directly related to the principles of the Bauhaus. Neues Sehen considered photography to be an autonomous artistic practice with its own laws of composition and lighting, through which the lens of the camera beco...

Koordinat: 41°46′N 101°09′E / 41.767°N 101.150°E / 41.767; 101.150 Tembok Khara-Khoto. Khara-Khoto (bahasa Mongolia: Khar Khot Kota Hitam)[1] adalah sebuah kota Tangut dahulu yang kini berada di daerah Kabupaten (qí) Ejin di Alxa, Mongolia Dalam di dekat Cekungan Danau Juyan. Khara-Khoto diketahui adalah Etzina yang disebut oleh Marco Polo. Nama Kabupaten Ejin sekarang diberikan atas nama kota ini. Nama Khara-Khoto memiliki banyak nama di antaranya...
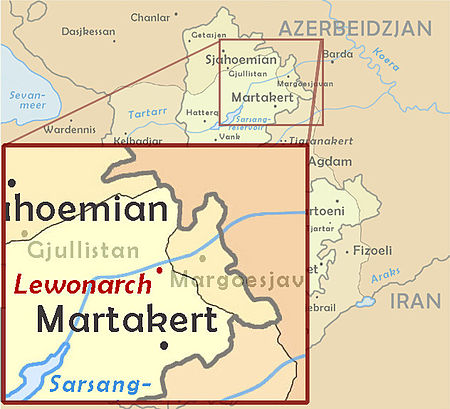
2008 Mardakert clashesPart of Nagorno-Karabakh conflictNKR, Mardakert, and the line of contactDate4 March 2008LocationMardakert/Aghdara, Nagorno-Karabakh RepublicResult Both sides claim victory Azerbaijan removes its troopsBelligerents Artsakh AzerbaijanCommanders and leaders Movses Hakobyan Najmaddin SadigovStrength Unknown Unknown, armored vehiclesCasualties and losses Per Armenia: 2 wounded[1]Per Azerbaijan:12 killed, 15 wounded[2][3] Per Azerbaijan: 4 ...

Autoritratto (1629) Wybrand Simonszoon de Geest I (Leeuwarden, 16 agosto 1592 – Leeuwarden, 1662) è stato un pittore olandese del secolo d'oro specializzato nella pittura di ritratti. Indice 1 Biografia 2 Opere 3 Note 4 Bibliografia 5 Voci correlate 6 Altri progetti 7 Collegamenti esterni Biografia Guglielmo Federico di Nassau-Dietz (1632) Era figlio di Simon Juckeszoon, pittore di vetrate[1], originario d'Anversa, che fu anche il suo primo maestro nell'arte della pittura[2]...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

Ne pas confondre avec le théorème de Cayley en théorie des groupes ni avec le théorème de Hamilton en géométrie. Portrait d'Arthur Cayley En algèbre linéaire, le théorème de Cayley-Hamilton affirme que tout endomorphisme d'un espace vectoriel de dimension finie sur un corps commutatif quelconque annule son propre polynôme caractéristique. En termes de matrice, cela signifie que si A est une matrice carrée d'ordre n et si p ( X ) = det ( X I n − A ) = X n + p n − 1...

For Netflix original series and related specials, see List of Netflix original programming. For Netflix original stand-up comedy specials, see List of Netflix original stand-up comedy specials. For Netflix exclusive international distribution films, see Lists of Netflix exclusive international distribution programming. Netflix is an American global on-demand Internet streaming media provider, that has distributed a number of original programs, including original series, specials, miniseries,...

The following list sorts all the cities in the Pakistani province of Punjab with a population of more than 100,000 according to the 2017 Census. As of 15 March 2017, 58 cities fulfill this criterion and are listed here. This list refers only to the population of individual cities, municipalities and towns within their defined limits, which does not include other municipalities or suburban areas within Urban agglomerations. List Jallah JeemLahore Faisalabad Rawalpindi Gujranwala Multan Sargod...

1922 film The Strangers' BanquetClaire Windsor, Hobart Bosworth, and TeddyDirected byMarshall NeilanWritten byMarshall NeilanFrank UrsonBased onThe Strangers' Banquetby Brian Oswald Donn-ByrneProduced byMarshall NeilanStarringHobart BosworthClaire WindsorRockliffe FellowesCinematographyMax FabianDavid KessonProductioncompanyMarshall Neilan ProductionsDistributed byGoldwyn PicturesRelease date December 31, 1922 (1922-12-31) Running time80 minutesCountryUnited StatesLanguageSilen...

Philips respiratory equipment division RespironicsCompany typeSubsidiaryIndustryMedicalFounded1976FounderGerald McGinnisHeadquartersMurrysville, PennsylvaniaKey peopleDon Spence, President and CEOProductsrespiratory equipmentsleep aidsRevenue $1.05 billion USDNumber of employees4,900[1]ParentPhilipsWebsitewww.respironics.com Respironics is an American medical supply company owned by Philips that specializes in products that improve respiratory functions. It is based in the Pittsburgh ...

Alcuni oggetti studiati in analisi matematica Funzioni Limiti Derivate Integrali Equazioni differenziali Funzioni a più variabili Funzioni complesse Campi vettoriali L'analisi matematica è il campo della matematica che si occupa delle proprietà che emergono dalla scomposizione infinita di un insieme denso. Si fonda sul calcolo infinitesimale, con il quale, attraverso le nozioni di limite e continuità, studia il comportamento locale di una funzione utilizzando gli strumenti del calcol...

American figure skater and diplomat (born 1980) Michelle KwanKwan in 2022United States Ambassador to BelizeIncumbentAssumed office December 5, 2022PresidentJoe BidenPreceded byLeyla Moses-Ones (chargé d'affaires) Personal detailsBorn (1980-07-07) July 7, 1980 (age 43)Torrance, California, U.S.Height5 ft 2 in (157 cm)Spouse Clay Pell (m. 2013; div. 2017)Children1Residence(s)California, U.S.Figure skating careerCountry...

Not to be confused with Kayaderasseras Creek. River in New York, United StatesKayaderosseras CreekKayaderosseras Creek looking downstream from US Route 9, April 2012LocationCountryUnited StatesStateNew YorkRegionUpstate New YorkMetropolitan areaCapital DistrictCountiesSaratoga CountyPhysical characteristicsSource • locationCorinth, Saratoga County, New York • coordinates43°12′00″N 73°55′17″W / 43.20000°N 73.92139°W...

Railway station in Merthyr Tydfil, Wales Quakers YardWelsh: Mynwent y CrynwyrQuakers Yard railway station in 2024General informationLocationQuakers Yard, Treharris, Merthyr TydfilWalesCoordinates51°39′37″N 3°19′23″W / 51.6604°N 3.3231°W / 51.6604; -3.3231Grid referenceST085965Managed byTransport for WalesPlatforms2Other informationStation codeQYDClassificationDfT category F2Key dates5 January 1858OpenedPassengers2018/19 65,7982019/20 59,8902020/21 10,764202...
Nennslingen. Nennslingen adalah kota yang terletak di distrik Weißenburg-Gunzenhausen di Bavaria, Jerman. Kota Nennslingen memiliki luas sebesar 21.97 km² . Nennslingen pada tahun 2006, memiliki penduduk sebanyak 1.395 jiwa. lbsKota dan kotamadya di Weissenburg-GunzenhausenAbsberg | Alesheim | Bergen | Burgsalach | Dittenheim | Ellingen | Ettenstatt | Gnotzheim | Gunzenhausen | Haundorf | Heidenheim | Höttingen | Langenalthei...

Computer font that maps glyphs to code points defined in the Unicode Standard A Unicode font is a computer font that maps glyphs to code points defined in the Unicode Standard.[1] The vast majority of modern computer fonts use Unicode mappings, even those fonts which only include glyphs for a single writing system, or even only support the basic Latin alphabet. Fonts which support a wide range of Unicode scripts and Unicode symbols are sometimes referred to as pan-Unicode fonts, altho...

Mountain classification of bicycle cycling in Italy Mountains classification in the Giro d'ItaliaGiulio Ciccone in the blue jersey of classification leader during the 2019 Giro d'ItaliaSportRoad CyclingCompetitionGiro d'ItaliaAwarded forBest climber in mountain stagesLocal nameGran Premio della Montagna (Italian)HistoryFirst award1933Editions87 (as of 2024)First winner Alfredo Binda (ITA)Most wins Gino Bartali (ITA)(7 wins)Most recent Tadej Pogacar (SLO) The Moun...