Nanomechanics
|
Read other articles:

Berkas:Sharepoint Designer.pngMicrosoft Office SharePoint Designer SharePoint adalah sebuah platform sistem manajemen dokumen berbasis web yang diciptakan oleh Microsoft Corporation. SharePoint dapat digunakan untuk menjalankan situs-situs web yang terdiri atas ruangan kerja (shared workspace) dan dokumen yang digunakan secara bersama-sama (shared documents), selain tentunya aplikasi khusus seperti wiki dan blog. Fitur-fitur SharePoint ini bisa diakses oleh sebuah penjelajah web (meski yang ...

Video game seriesOne Piece video gamesGenre(s)Action-adventure, fighting, role-playingDeveloper(s)VariousPublisher(s)BandaiBandai Namco EntertainmentComposer(s)VariousPlatform(s)WonderSwan, PlayStation, Game Boy Color, WonderSwan Color, Game Boy Advance, PlayStation 2, GameCube, Wii, Nintendo DS, PlayStation Portable, Nintendo 3DS, Nintendo Switch, PlayStation 3, Wii U, PlayStation 4, PlayStation Vita, Windows, iOS, Android, Xbox One, PlayStation VRFirst releaseFrom TV Animation - One Piece:...

Logo YKS Romantic Award 2014 YKS Romantic Award 2014 adalah ajang penghargaan yang dilaksanakan oleh Yuk Keep Smile di Trans TV. Pelaksanaan ajang penghargaan ini bertepatan dengan Hari Kasih Sayang yang biasa diperingati oleh anak muda tanggal 14 Februari setiap tahunnya. Nominator dan Kategori Nominator Kebanyakan nominator didominasi dari orang-orang yang terlibat dalam acara Yuk Keep Smile, seperti pengisi acara, bintang tamu, dan juga crew yang terlibat. Kategori Penampilan Terkejut Raff...
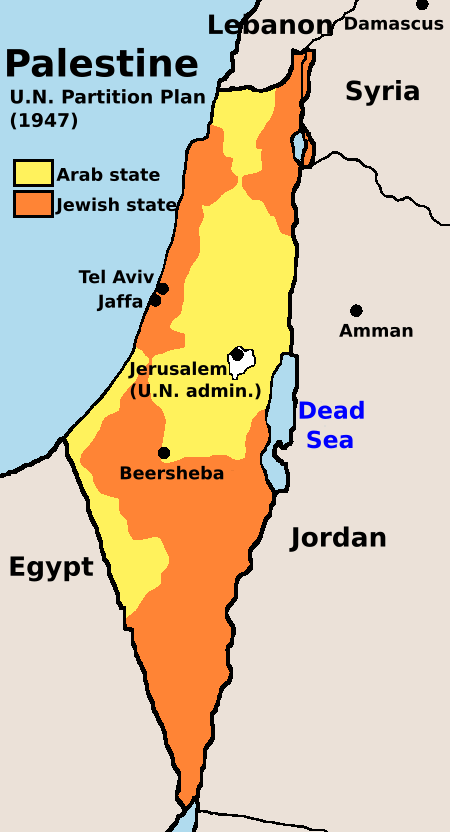
Artikel ini sudah memiliki daftar referensi, bacaan terkait, atau pranala luar, tetapi sumbernya belum jelas karena belum menyertakan kutipan pada kalimat. Mohon tingkatkan kualitas artikel ini dengan memasukkan rujukan yang lebih mendetail bila perlu. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Resolusi 181 (II)Majelis Umum PBBRencana Pembagian UNSCOP (3 September 1947; lihat garis hijau) dan Komite Ad Hoc PBB (25 November 1947). Proposal Komite Ad Hoc PBB dipilih dal...

Pour un article plus général, voir Attentats de janvier 2015 en France. Attentat contre Charlie Hebdo Journalistes, secouristes et policiers, rue Nicolas-Appert, après l'attaque au journal Charlie Hebdo. Localisation 10, rue Nicolas-Appert et boulevard Richard-Lenoir, 11e arrondissement de Paris, France Cible Collaborateurs de Charlie HebdoPoliciers Coordonnées 48° 51′ 33″ nord, 2° 22′ 13″ est Date 7 janvier 2015 Vers 11 h 30 (UTC+1)...

Questa voce sugli argomenti scrittori italiani e giornalisti italiani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti dei progetti di riferimento 1, 2. Sandro Camasio Sandro Camasio, all'anagrafe Alessandro Camasio (Isola della Scala, 5 aprile 1886 – Torino, 23 maggio 1913), è stato un giornalista, scrittore e regista italiano. Indice 1 Biografia 2 Opere 2.1 Opere teatrali 2.2 Film 3 Note 4 Bibliografia 5 Altri progetti 6 Colle...

American publishing house This article is about the publishing house. For the person, see Alfred A. Knopf Sr. For other people named Knopf, see Knopf (surname). Alfred A. KnopfParent companyPenguin Random HouseFounded1915; 109 years ago (1915)FounderBlanche Wolf Knopf and Alfred A. Knopf Sr.Country of originUnited StatesHeadquarters locationNew York City, U.S.Official websiteknopfdoubleday.com/imprint/knopf/ Alfred A. Knopf, Inc. (/knɒpf/) is an American publishing house th...
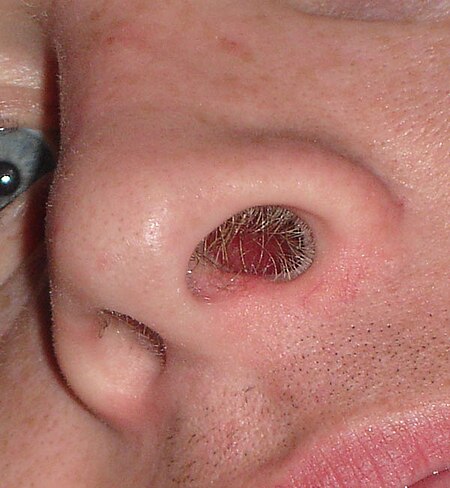
Hair in the nostrils of adult humans Nasal hair Nasal hair or nose hair is the hair in the human nose. Adult humans have hair in the nostrils. Nasal hair functions include filtering foreign particles from entering the nasal cavity, and collecting moisture.[1] In support of the first function, the results of a 2011 study indicated that increased nasal hair density decreases the development of asthma in those who have seasonal rhinitis, possibly due to an increased capacity of the hair ...

ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Раннее христианство Гностическое христианство Вселенские соборы Н...

2024 border incident in Texas Standoff at Eagle PassPart of Operation Lone StarLocation of Eagle Pass, Texas, within Maverick CountyDateJanuary 11, 2024 (2024-01-11) – presentLocationShelby Park, Eagle Pass, Texas, U.S.28°42′29″N 100°30′33″W / 28.7080°N 100.5092°W / 28.7080; -100.5092Caused byPolitical polarization in the United States; Mexico–United States border crisisStatusOngoingParties Federal government Department of Homeland Securi...

← березень → Пн Вт Ср Чт Пт Сб Нд 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 2024 рік 25 березня — 84-й день року (85-й у високосні роки) у григоріанському календарі. До кінця року залишається 281 день. Цей день в історії: 24 березня—25 березня—26 березня Зм�...

Path by which a drug, fluid, poison, or other substance is taken into the body Oral administration of a liquid. In pharmacology and toxicology, a route of administration is the way by which a drug, fluid, poison, or other substance is taken into the body.[1] Routes of administration are generally classified by the location at which the substance is applied. Common examples include oral and intravenous administration. Routes can also be classified based on where the target of action is...

Association football club in England Football clubDodworth Miners WelfareFull nameDodworth Miners Welfare Football ClubGroundMiners Welfare Ground, DodworthManagerLuke Forgione / Joshua WrightLeagueSheffield & Hallamshire County Senior League Premier Division2023–24Sheffield & Hallamshire County Senior League Premier Division, 2nd of 14 Home colours Dodworth Miners Welfare Football Club is a football club based in Dodworth, Barnsley, South Yorkshire, England. They are currently memb...

Franja de Gazaقطاع غزةQiṭāʿ Ġazzah Territorio Bandera Ubicación de la Franja de Gaza en el Estado de PalestinaCoordenadas 31°27′N 34°24′E / 31.45, 34.4Capital GazaEntidad Territorio • País Palestina PalestinaEventos históricos • Fundación 1993Superficie • Total 365 km² Población • Total 2,047,969 hab. • Densidad 5,046 hab./km²Gentilicio gazatíHuso horario UTC+02:00 y UTC+03:00[...

5th-century Christian mystic and saint SaintPoemen the GreatVenerableBornc. 340Province of Egypt, Roman EmpireDiedc. 450Wadi El Natrun, Province of Egypt, Roman EmpireVenerated inEastern Orthodox ChurchOriental Orthodox ChurchesRoman Catholic ChurchFeast27 AugustAttributeshermit, ascetic Part of a series onChristian mysticism Theology and philosophy Apophatic Ascetical Cataphatic Catholic spirituality Hellenistic Mystical theology Neoplatonic Henosis Practices Monasticism Monasticism New...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Coat of arms of Brazil – news · newspapers · books · scholar · JSTOR (May 2020) (Learn how and when to remove this message) Coat of arms of BrazilVersionsRarely used version with a dark blue color ArmigerFederative Republic of BrazilAdopted11 May 1992Supporter...

2016 live album by George CarlinI Kinda Like It When a Lotta People DieLive album by George CarlinReleasedSeptember 16, 2016Recorded1957 (Boston Rant)June 23, 2001 (Bonus track)September 9 & 10, 2001 (Main show)2016 (Interviews)[1]GenreComedyLength56:18LabelEardrum/MPI MediaProducerGeorge CarlinGeorge Carlin chronology It's Bad for Ya(2008) I Kinda Like It When a Lotta People Die(2016) I Kinda Like It When a Lotta People Die is the 20th and final album by American stand-up...

Association football club in England This article is about the football team from Nottingham. For the former team from Bristol, see Clifton Association F.C. Football clubClifton All WhitesFull nameClifton All Whites Football ClubNickname(s)CFC, All Whites, WhitesFounded1963GroundNorman Archer Memorial, CliftonOwnerYoung Boys ClubsChairmanRichard HipkissManagerJames TurnerLeagueUnited Counties League Division One2023–24United Counties League Division One, 13th of 21WebsiteClub website Home c...

Place in Upper Austria, AustriaKönigswiesen Coat of armsKönigswiesenLocation within AustriaCoordinates: 48°24′28″N 14°50′29″E / 48.40778°N 14.84139°E / 48.40778; 14.84139CountryAustriaStateUpper AustriaDistrictFreistadtGovernment • MayorJohann Holzmann (ÖVP)Area[1] • Total73.41 km2 (28.34 sq mi)Elevation614 m (2,014 ft)Population (2018-01-01)[2] • Total3,113 • D...

A contemporary engraving of John Price by Wenceslas Hollar John Price (Pricaeus) (c. 1602–1676) was an English classical scholar, publisher and collector of books. He was a Roman Catholic who described himself as ‘Anglo-Britannus’.[1] In 1635, in Paris, he published the Apologia of Apuleius.[1] From 1652 the Medicis employed him as their keeper of coins. He was also appointed professor of Greek at Pisa.[1] In 1661 he moved, under patronage of Cardinal Francesco ...