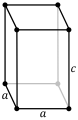
Magnetocrystalline anisotropy
|
Read other articles:

Katedral NanjingKatedral Perawan Maria Dikandung Tanpa Noda, NanjingHanzi: 圣母无染原罪始胎堂Katedral NanjingKoordinat: 32°02′27″N 118°46′42″E / 32.04083°N 118.77833°E / 32.04083; 118.77833Lokasi112 Jalan Shigu, NanjingNegaraTiongkokDenominasiGereja Katolik RomaArsitekturStatusKatedralStatus fungsionalAktifAdministrasiKeuskupan AgungKeuskupan Agung Nanjing Katedral Nanjing atau yang bernama resmi Katedral Santa Perawan Maria Dikandung Tanpa Nod...

Untuk pola warna, lihat polkadot. PolkadotTipeperangkat lunak dan mata uang kripto BerdasarkaSubstrate (en) Versi pertama2020 Versi stabil 1.0.0 (19 Juli 2023) Informasi pengembangPembuatWeb3 FoundationPengembangParity Technologies LTD.Sumber kode Kode sumberPranala Informasi tambahanSitus webhttps://polkadot.networkSubredditPolkadot Sunting di Wikidata • L • B • Bantuan penggunaan templat ini Polkadot adalah usulan pertukaran multi-rantai heterogen dan terjemahan arsitek...

25N-NBOMe Names Preferred IUPAC name 2-(2,5-Dimethoxy-4-nitrophenyl)-N-[(2-methoxyphenyl)methyl]ethan-1-amine Other names 2C-N-NBOMe, NBOMe-2C-N Identifiers CAS Number 1354632-03-3 3D model (JSmol) Interactive image ChemSpider 52085577 PubChem CID 118536028 UNII 0G7SSW2N0S Y CompTox Dashboard (EPA) DTXSID501014186 InChI InChI=1S/C18H22N2O5/c1-23-16-7-5-4-6-14(16)12-19-9-8-13-10-18(25-3)15(20(21)22)11-17(13)24-2/h4-7,10-11,19H,8-9,12H2,1-3H3Key: TXCKTIBHURMASQ-UHFFFAOYSA-N SMILES CO...

Kongregasi Misionaris Putra Hati Kudus Bunda Perawan MariaClaretianCongregatio Missionariorum Filiorum Immaculati Cordis Beatae Mariae VirginisSingkatanCMFTanggal pendirian16 Juli 1849PendiriSanto Antonius Maria KlaretTipeOrdo keagamaan Katolik (Lembaga Kehidupan Tahbisan)Kantor pusatVia del Sacro Cuore di Maria, 5, 00197 Roma, ItaliaSitus webclaret.org Klaresia, sebuah komunitas imam dan bruder Katolik Roma, didirikan oleh Santo Antonius Klaret pada 1849. Karya mereka sangat beragam dan terg...

Voce principale: Avezzano Calcio. Football Club AvezzanoStagione 1978-1979Sport calcio Squadra Avezzano Allenatore Feliciano Orazi Franco Panzieri Guido Liberati Presidente Ugo Graziani Francesco Fedele e Gino Lolli Serie C216º posto nel girone C. 1977-1978 1979-1980 Si invita a seguire il modello di voce Questa pagina raccoglie le informazioni riguardanti il Football Club Avezzano nelle competizioni ufficiali della stagione 1978-1979. Stadio dei Marsi di Avezzano Indice 1 Rosa 1.1 Ros...

ロバート・デ・ニーロRobert De Niro 2011年のデ・ニーロ生年月日 (1943-08-17) 1943年8月17日(80歳)出生地 アメリカ合衆国・ニューヨーク州ニューヨーク市身長 177 cm職業 俳優、映画監督、映画プロデューサージャンル 映画、テレビドラマ活動期間 1963年 -配偶者 ダイアン・アボット(1976年 - 1988年)グレイス・ハイタワー(1997年 - )主な作品 『ミーン・ストリート』(1973年)...

35 mm photographic film format This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 135 film – news · newspapers · books · scholar · JSTOR (March 2014) (Learn how and when to remove this message) 135 film. The film is 35 mm (1.4 in) wide. Each image is 24×36 mm in the most common small film format...

Cargo ship built in Denmark in World War 2 Gotenland History Name 1942: Gotenland 1945: Hopeville 1967: Oinoussian Hope 1968: Esperanza Owner 1942: Kriegsmarine 1945: Skibs-A/S Steinstad 1957: Skibs-A/S Siljestad 1967: Argyros Cia SA Operator 1942: Norddeutscher Lloyd 1945: A. F. Klaveness & Co 1967: Panagiotis A Lemos & Co Ltd Port of registry 1942: 1945: Oslo 1967: Piraeus BuilderBurmeister & Wain, Copenhagen Laid down1940 CompletedNovember 1942 Identification 1945: call sign LL...

American film director, producer and screenwriter (born 1960) Richard LinklaterLinklater in 2015BornRichard Stuart Linklater (1960-07-30) July 30, 1960 (age 63)Houston, Texas, U.S.Occupation(s)Director, producer, writerYears active1985–present[1]Notable workBoyhood, Dazed and Confused, Before trilogy, School of Rock, Waking Life, SlackerSpouseChristina HarrisonChildren3, including LoreleiWebsitedetourfilm.com Richard Stuart Linklater (/ˈlɪŋkleɪtər/; born July 30, 1960...

Indigenous Maya people of Guatemala Kaqchikel (Cakchiquel)A Kaqchikel familyTotal population1,068,356[1]Regions with significant populations Guatemala (Sacatepéquez, Sololá) Mexico (Chiapas, Campeche)LanguagesKaqchikel, SpanishReligionCatholic, Evangelical, Maya religionRelated ethnic groupsK'iche', Tzutujil The Kaqchikel (also called Kachiquel[2]) are one of the Indigenous Maya peoples of the midwestern highlands of Guatemala and of southern Mexico. They constitut...

Dick SutherlandSutherland (tengah) dengan Mildred Davis dan Harold Lloyd (di air), A Sailor-Made Man (1921)LahirArchibald Thomas Johnson(1881-12-23)23 Desember 1881Benton, Kentucky, Amerika SerikatMeninggal3 Februari 1934(1934-02-03) (umur 52)Hollywood, California, Amerika SerikatPekerjaanPemeranTahun aktif1921-1932 Dick Sutherland (nama lahir Archibald Thomas Johnson, 23 Desember 1881 – 3 Februari 1934) adalah seorang pemeran film Amerika Serikat, yang banyak berka...

هرقل نصف إله هو كائن إلهي أو خارق في الميثولوجيا الكلاسيكية.[1][2][3] وقد استخدم هذا المصطلح في طرق مختلفة في أزمنة مختلفة، ويصف شخصية بلغت منزلة إلهية بعد الموت، أو إله أقل مرتبة، أو بشر من نسل إله وإنسان. كما وتتصف شخصية نصف إله بالخلوذ والأبدية. من أنصاف الآلهة: ج...

У Вікіпедії є статті про інші значення цього терміна: Ягорлик (значення). Ягорлик Ягорлик у селі Довжанка47°22′59″ пн. ш. 29°11′33″ сх. д. / 47.38310000002777400° пн. ш. 29.19270000002777721° сх. д. / 47.38310000002777400; 29.19270000002777721Витік на схід від смт Слобідки• координати ...

Abbasid-era library in Baghdad, modern-day Iraq This article is about the Abbasid library in Baghdad, Iraq. For the Fatimid library in Cairo, Egypt, see House of Knowledge. House of Wisdomبَيْت الْحِكْمَةScholars at the Abbasid library (Maqamat al-Hariri)Illustration by Yahya ibn Mahmud al-Wasiti, 1237LocationBaghdad, Abbasid Caliphate (now Iraq)TypeLibraryEstablishedc. 8th century CEDissolved1258 (Mongol conquest) The House of Wisdom (Arabic: بَيْت الْحِ...

此條目没有列出任何参考或来源。 (2022年3月11日)維基百科所有的內容都應該可供查證。请协助補充可靠来源以改善这篇条目。无法查证的內容可能會因為異議提出而被移除。 政治主題的一部分選舉/投票制度 多數/複數制 多數制 領先者當選 不可轉移單票制 有限投票制 全票制 總選票 多輪選舉制 两轮选举制 多輪絕對多數制 排序投票制 排序複選制 權變投票制(英语:Conti...

President of the Dominican Republic (1906–2002) In this Spanish name, the first or paternal surname is Balaguer and the second or maternal family name is Ricardo. The DoctorJoaquín BalaguerBalaguer in 1977President of the Dominican RepublicIn office16 August 1986 – 16 August 1996Vice PresidentCarlos Morales TroncosoJacinto Peynado GarrigosaPreceded bySalvador Jorge BlancoSucceeded byLeonel FernándezIn office1 July 1966 – 16 August 1978Vice PresidentFrancisco ...

This is an alphabetical listing of notable mosques in the United States (Arabic: Masjid, Spanish: Mezquita), including Islamic places of worship that do not qualify as traditional mosques. History of mosques in the United States Number of mosques per million residents in each U.S. state and the District of Columbia as of 2020 A mosque, also called masjid in Arabic, is defined as any place where Muslims pray facing Mecca, not necessarily a building. By that meaning, there were mosques in the ...

مقاطعة ودفورد الإحداثيات 38°02′N 84°44′W / 38.04°N 84.74°W / 38.04; -84.74 [1] تاريخ التأسيس 2 نوفمبر 1788 تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى كنتاكي العاصمة فرسايليس خصائص جغرافية المساحة 497 كيلومتر مربع عدد السكان ع...

John Francis Clauserジョン・フランシス・クラウザー 生誕 (1942-12-01) 1942年12月1日(81歳) アメリカ合衆国 カリフォルニア州パサデナ国籍 アメリカ合衆国研究機関 ローレンス・バークレー国立研究所ローレンス・リバモア国立研究所カリフォルニア大学バークレー校出身校 カリフォルニア工科大学コロンビア大学主な受賞歴 ウルフ賞物理学部門(2010)ノーベル物理学賞(2022)プ...

1513 painting by Palma Vecchio Assumption of the VirginItalian: Assunzione della VergineArtistPalma VecchioYearc. 1513MediumOil on panelDimensions191 cm × 137 cm (75 in × 54 in)LocationGallerie dell'Accademia, Venice The Assumption of the Virgin is an oil on panel painting by Palma Vecchio, created c. 1513, now in the Gallerie dell'Accademia in Venice.[1][2] It shows an episode recounted in the apocryphal gospels - the Virgin M...