Law of truly large numbers
|
Read other articles:

Kue mungil atau kue kecil (Bahasa Prancis: petit four; mignardises) adalah penganan manis atau penyelera gurih berukuran kecil atau mungil. Anekaragam kue mungil Jenis Kue kecil terdiri dari beberapa jenis seperti berikut: P terdiri dari tiga jenis: Glacé (bersalut), kue kecil berhias atau dihias yang dilapisi fondan atau icing, seperti éclair kecil, dan tartlet Salé (asin), makanan pembuka seukuran gigitan yang gurih biasanya disajikan di pesta koktail atau prasmanan Sec (kering), biskuit...

العلاقات الجنوب أفريقية الفرنسية جنوب أفريقيا فرنسا جنوب أفريقيا فرنسا تعديل مصدري - تعديل العلاقات الجنوب أفريقية الفرنسية هي العلاقات الثنائية التي تجمع بين جنوب أفريقيا وفرنسا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية ...

H.Tri KurniadiS.H., M.Si.Berkas:Walkot Jaksel Tri Kurniadi.jpg Wali Kota Administrasi Jakarta Selatan ke-14Masa jabatan13 Agustus 2015 – 5 Juli 2018PresidenJoko WidodoGubernurBasuki Tjahaja Purnama Djarot Saiful Hidayat Anies BaswedanWakilArifin PendahuluSyamsuddin NoorPenggantiMarullah MataliWakil Wali Kota Jakarta SelatanMasa jabatan2 Januari 2015 – 13 Agustus 2015PresidenJoko WidodoGubernurBasuki Tjahaja PurnamaWali KotaSyamsuddin Noor PendahuluTri Djoko Sri Margi...

Stasiun Myōon-dōri妙音通駅Lokasi3-9 Myōon-dōri, Mizuho, Nagoya, Aichi(名古屋市瑞穂区妙音通三丁目9)JepangOperatorBiro Transportasi Kota NagoyaJalurJalur MeijōLayanan Pemberhentian bus Informasi lainKode stasiunM24SejarahDibuka1974Penumpang20091938 per hari Sunting kotak info • L • BBantuan penggunaan templat ini Stasiun Myōon-dōri (妙音通駅code: ja is deprecated , Myōon-dōri-eki) adalah sebuah stasiun metro bawah tanah yang terletak di Mizuho-ku,...

تاريخ الفلسفةمخطوط عربي في الكيمياء يذكر أصحاب «الصنعة» بأنهم «فلاسفة»معلومات عامةوصفها المصدر قاموس بروكهاوس وإفرون الموسوعي التأثيراتأحد جوانب فلسفة فرع من علم التاريخفلسفة تعديل - تعديل مصدري - تعديل ويكي بيانات تنقسم دراسة تاريخ الفلسفة تقليدياً إلى ثلاث مراحل: الع�...
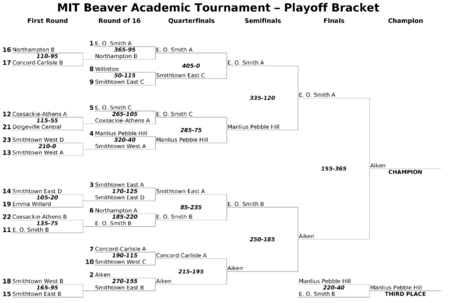
Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Sistem gugur – berita · surat kabar · buku · cendekiawan · JSTOR Contoh penjadwalan turnamen dengan sistem gugur. Sistem gugur (atau Sistem Knockout atau sistem KO) merupakan salah satu format turnamen y...

Bahasa Xiang 湘語/湘语 Bahasa HsiangBahasa Hunan Bahasa Xiang dalam aksara Han tradisional (kiri) dan aksara Han sederhana (kanan) Dituturkan diRepublik Rakyat TiongkokWilayahHunan tengah dan barat daya, Guangxi utara, sebagian Guizhou dan HubeiEtnisOrang HunanPenutur38 juta (2007)[1] Rincian data penutur Jumlah penutur beserta (jika ada) metode pengambilan, jenis, tanggal, dan tempat.[2] 37.300.000 (2019, Bahasa ibu)36.000.000 (1984) Rumpun bahasaSino-Tibet Tion...

Cet article est une ébauche concernant Tokyo. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Yūrakuchō有楽町 Administration Pays Japon Ville Tokyo Arrondissement Chiyoda Géographie Coordonnées 35° 39′ 54″ nord, 139° 45′ 38″ est Localisation Géolocalisation sur la carte : Tokyo Yūrakuchō有楽町 Géolocalisation sur la carte : Japon Yūrakuchō有楽�...

Questa voce o sezione sull'argomento Germania non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Questa voce sull'argomento Meclemburgo-Pomerania Anteriore è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. La Terra dei laghi del Meclemburgo in un'immagine aerea La Terra...

Questa voce sull'argomento stagioni delle società calcistiche greche è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Voce principale: Athlītikī Enōsī Larisas 1964. Athlītikī Enōsī Larisas 1964Stagione 2017-2018Sport calcio Squadra Larissa Allenatore Sotiris Antoniu Souper Ligka Ellada11º posto Coppa di GreciaSemifinali StadioAEL FC Arena (16 118) 2016-2017 2018-2019 Si invita a seguire il modello di voce Questa voce raccoglie le in...

Saint-Médard-la-RochettecomuneSaint-Médard-la-Rochette – Veduta LocalizzazioneStato Francia Regione Nuova Aquitania Dipartimento Creuse ArrondissementAubusson CantoneGouzon TerritorioCoordinate46°02′41″N 2°08′49″E / 46.044722°N 2.146944°E46.044722; 2.146944 (Saint-Médard-la-Rochette)Coordinate: 46°02′41″N 2°08′49″E / 46.044722°N 2.146944°E46.044722; 2.146944 (Saint-Médard-la-Rochette) Altitudine570 m s....

SaentisDesaNegara IndonesiaProvinsiSumatera UtaraKabupatenDeli SerdangKecamatanPercut Sei TuanKode pos20371Kode Kemendagri12.07.26.2009 Luas2400 Ha.Jumlah penduduk16.727 jiwa (2013)Kepadatan- Hutan dan Tanaman Rotan di Saentis - 1917 Saentis adalah desa di kecamatan Percut Sei Tuan, Kabupaten Deli Serdang, Sumatera Utara, Indonesia. Disini Terdapat tempat pengeraman tembakau yang dibangun pada tahun 1920 pada masa Hindia Belanda. KONDISI UMUM GEOGRAFIS Desa Saentis merupakan salah satu k...

Cet article est une ébauche concernant la politique. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Le concept est employé par Maajid Nawaz pour décrire une partie de la gauche qui ne s'oppose pas aux régressions de certains groupes culturels. La gauche régressive est une épithète utilisée pour décrire une partie de la gauche politique accusée de tenir une position contradictoire en tolérant ou en fa...

Restricted traffic lane HOV and HOV Lane redirect here. For the song by Nicki Minaj, see Pink Friday: Roman Reloaded. For other uses, see HOV (disambiguation). This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article's tone or style may not reflect the encyclopedic tone used on Wikipedia. See Wikipedia's guide to writing better articles for suggestions. (January 2023) (Learn how and w...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要擴充。 (2013年1月1日)请協助改善这篇條目,更進一步的信息可能會在討論頁或扩充请求中找到。请在擴充條目後將此模板移除。 此條目需要补充更多来源。 (2013年1月1日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

2001 novel Anne Frank and Me First editionAuthorCherie Bennett and Jeff GottesfeldLanguageEnglishGenreHistorical fiction, Teenage literaturePublisherPutnamPublication dateNovember, 2001Publication placeUnited StatesMedia typePrint (Paperback)Pages291 p.ISBN0-439-37131-7 Anne Frank and Me is a 2001 novel by husband and wife writing team Cherie Bennett and Jeff Gottesfeld. Inspired by the life of Anne Frank, it follows a teenage girl named Nicole Burns who travels back in time to 1942 and ...

Susquehanna Trail marker Older Susquehanna Trail marker The Susquehanna Trail was an auto trail in the United States linking Washington, D.C., with Niagara Falls, New York. It passed through Baltimore, Maryland; Harrisburg, Pennsylvania; Williamsport, Pennsylvania; and Buffalo, New York. In relatively modern terms, the Susquehanna Trail roughly followed the following highways: U.S. Route 1, Washington, D.C., to Baltimore, Maryland U.S. Route 111 (now MD Route 45, Interstate 83 Business and ot...

Raid on Godfrey RanchPart of the Colorado WarDateJanuary 15, 1865LocationColorado Territory40°26′36.6″N 103°22′45.2″W / 40.443500°N 103.379222°W / 40.443500; -103.379222Result United States victoryIndians retreatBelligerents United States LakotaCheyenneCommanders and leaders Holon Godfrey UnknownStrength 3 men[1] 130 warriorsCasualties and losses None 3-17 killed[2][3] vteColorado War Hungate massacre (June 11, 1864) Sand Creek...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (نوفمبر 2019) كأس إيطاليا 1975–76 تفاصيل الموسم كأس إيطاليا النسخة 29 البلد إيطاليا التاريخ بداية:27 أغسطس 1975 ...
