Langlands–Shahidi method
|
Read other articles:

غثيان وقيء بعد العملية الجراحية معلومات عامة من أنواع غثيان، ومضاعفات بعد العمليات [لغات أخرى] الإدارة أدوية ميتوكلوبراميد تعديل مصدري - تعديل الغثيان والقيء بعد العملية الجراحية هي المضاعفات التي تؤثر على حوالي 10% من الأشخاص الذين يخضعون للتخدير ا...

Paralimpiade XTuan rumahAtlanta, Amerika SerikatMotoThe Triumph of the Human SpiritJumlah negara104Jumlah atlet3.259Jumlah disiplin517 dalam 20 cabang olahragaPembukaan16 Agustus 1996Penutupan25 Agustus 1996Dibuka olehAl Gore, Wakil Presiden ASKaldronMark WellmanStadionStadion Olimpiade CentennialMusim Panas Olimpiade: Atlanta 1996 ← Barcelona 1992 Sydney 2000 → Musim Dingin ← Lillehammer 1994 Nagano 1998 → Paralimpiade Musim Panas 1996 (Paralimpiade Musim Panas X) ada...

Irish censorship and classification within Ireland This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Irish Film Classification Office – news · newspapers · books · scholar · JSTOR (February 2012) (Learn how and when to remove this template message) Irish Film Classification OfficeOifig Aicmithe Scannán na hÉ...

Serbian patriarch Mihailo DožićHegumen of Morača MonasteryNative nameМихаилоChurchSerbian Orthodox ChurchElected5 March 1879Installed10 March 1879 (Morača Monastery)Term ended9 June 1914OrdersOrdination20 May 1865Consecration5 March 1879by Ilarion RoganovićRankArchimandritePersonal detailsBornMilovan Dožić(1848-11-15)15 November 1848Vrujci, Kolašin Municipality, Principality of SerbiaDied9 June 1914(1914-06-09) (aged 65)Morača Monastery, Kingdom of SerbiaBuriedMorač...

Questa voce o sezione sull'argomento nobili tedeschi non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Simone Enrico AdolfoRitratto del conte Simone Enrico Adolfo di Lippe-DetmoldConte di Lippe-DetmoldStemma In carica1718 - 1734 PredecessoreFederico Adolfo SuccessoreSimone Augusto TrattamentoSua altezza serenissima NascitaDetmold, 25 gennaio 1694 Mor...

1946 1956 Élections législatives de 1951 dans l'Aube le 17 juin 1951 Type d’élection Élection législative Postes à élire 4 députés modifier - modifier le code - voir Wikidata Les élections législatives françaises de 1951 se tiennent le 17 juin. Ce sont les deuxièmes élections législatives de la Quatrième République. Mode de Scrutin Représentation proportionnelle plurinominale suivant la méthode du plus fort reste dans 103 circonscriptions, conformément à la ...

Submachine gun Type 77 submachine gun TypeSubmachine gunPlace of originTaiwan (Republic of China)Production historyDesigned1985ManufacturerHsing Hua ArsenalSpecificationsMass2.82 kg emptyLength 335 mm (13.19 in) with stock folded 610 mm (24.02 in) with stock extended Barrel length215 mm (8.46 in)Cartridge9×19mm ParabellumCaliber9 mmActionBlowbackRate of fire1200-1500 RPMMaximum firing range150 m (492 ft)Feed syst...

Australian film and culture award ceremony This article contains content that is written like an advertisement. Please help improve it by removing promotional content and inappropriate external links, and by adding encyclopedic content written from a neutral point of view. (February 2019) (Learn how and when to remove this message) Asia Pacific Screen AwardsCurrent: 16th Asia Pacific Screen AwardsAsia Pacific Screen Awards logoAwarded forBest in film and documentary in the Asia-Pacific region...

Tiziano Pieri Informazioni personali Arbitro di Calcio Sezione Lucca Attività nazionale Anni Campionato Ruolo 2001-2008 Serie A arbitro Tiziano Pieri (Genova, 16 novembre 1971) è un ex arbitro di calcio italiano. Biografia Iscritto alla sezione AIA di Genova, dal 2002 a quella di Lucca, ha esordito in Serie A il 16 settembre 2001 in Fiorentina-Atalanta terminata 3-1. Nel gennaio 2006 arriva la nomina ad arbitro internazionale, però, dopo pochi mesi viene coinvolto nell'inchiesta nota come...

Pour les articles homonymes, voir Star Trek (homonymie). Logo de la série télévisée Star Trek. Cette section doit être actualisée. Des passages de cette section sont obsolètes ou annoncent des événements désormais passés. Améliorez-la ou discutez-en. Star Trek[n 1] (à l'origine nommée sous son titre français, Patrouille du cosmos) est un univers de science-fiction, créé par Gene Roddenberry en 1966, qui regroupe sept séries télévisées qui comptabilisent 788 épisodes[...

No. 334 (Norwegian) Squadron RAFde Havilland MosquitoActive1945CountryUnited KingdomAllegianceNorwegian Government in exileBranchRoyal Air ForceNickname(s)NorwegianMilitary unit No. 334 (Norwegian) Squadron was a Royal Air Force aircraft squadron that operated after the Second World War. Established after V-E Day, it soon became 334 Squadron of the Royal Norwegian Air Force.[1] History The squadron was formed on 26 May 1945 at RAF Banff, Scotland from B Flight of 333 Squadron.[2&...

Calvisson La mairie. Blason Administration Pays France Région Occitanie Département Gard Arrondissement Nîmes Intercommunalité Communauté de communes du Pays de Sommières Maire Mandat André Sauzède 2020-2026 Code postal 30420 Code commune 30062 Démographie Gentilé Calvissonais (ses) Populationmunicipale 6 105 hab. (2021 ) Densité 211 hab./km2 Géographie Coordonnées 43° 47′ 09″ nord, 4° 11′ 34″ est Altitude Min. 23 mMax....

Japanese-American Delta/SLS rocket part Delta Cryogenic Second StageA 4-meter DCSS from a Delta IV MediumManufacturerBoeing IDSUnited Launch AllianceMitsubishi Heavy Industries(Original Delta III design and manufacturing)JAXA/NASDA(H-IIA/DCSS upper stage design, original version)Country of originUnited StatesJapan (Delta III, original)Used onDelta IIIDelta IVSLS Block ILaunch historyStatusActiveTotal launches45Successes(stage only)4218 Delta IV 4 m23 Delta IV 5 mFailed2 (Delta III)L...

Provincial park in Ontario, Canada Aaron Provincial ParkIUCN category II (national park)To the south of Thunder Lake is the surrounding Aaron Provincial Park, camera viewing northLocation of Aaron Provincial Park in Ontario.LocationKenora, Ontario, CanadaCoordinates49°45′42.2″N 92°39′23.4″W / 49.761722°N 92.656500°W / 49.761722; -92.656500Area116 ha (290 acres)Elevation382 m (1,253 ft)Named forOriginal homestead of John. T. Aaron Aaron Provin...

Headquarters component of the U.S. Marine Corps' Marine Air-Ground Task Forces For the HTML element <command>, see HTML 5. USMC Combat Operations Center In the United States Marine Corps, the command element (CE) is the command and control force of a Marine Air-Ground Task Force (MAGTF). It provides C3I for the MAGTF. Role within the MAGTF The Command Element (CE), a headquarters unit organized into a MAGTF (MEU, MEB, MEF) headquarters (HQ) group, that exercises command and control (man...

Pour les articles homonymes, voir Durant. PhilBiographieNaissance 30 août 1964WahaDécès 18 avril 2012 (à 47 ans)LiègeSépulture LiègeNom de naissance Philippe DurantNationalité belgeActivités Auteur de bande dessinée, scénariste de bande dessinée, dessinateur humoristique, dessinateur de presseAutres informationsA travaillé pour SpirouPsikopatGenre artistique Bande dessinée alternativeBlog officiel philcomix.blogspot.comŒuvres principales Comix 2000modifier - modifier le c...
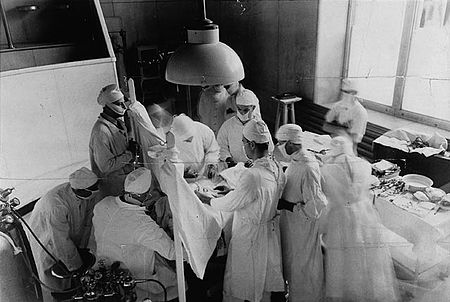
For other hospitals with the same name (see list), see Victoria Hospital. Hospital in Quebec, CanadaRoyal Victoria Hospital - GlenMcGill University Health CentreMcGill University Health Center's hospital complex - Glen siteLocation in Montreal (Glen site)GeographyLocation1001 Decarie Boulevard, Montreal, Quebec, CanadaCoordinates45°28′19″N 73°36′10″W / 45.471851°N 73.602716°W / 45.471851; -73.602716OrganizationCare systemPublic (RAMQ)TypeTeachingAffiliated ...

Cet article est une ébauche concernant l’astrophysique. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Pour les articles homonymes, voir Hayashi. Le trajet de Hayashi est une étude faite par l'astrophysicien japonais Chūshirō Hayashi sur les proto-étoiles et leur équilibre hydrostatique. Plus concrètement, c'est une ligne presque verticale sur la droite du diagramme de Hertzsprung-Russell, donc une rel...

San Giorgio e il dragoAutorePaolo Uccello Data1460 circa Tecnicaolio su tela Dimensioni57×73 cm UbicazioneNational Gallery, Londra San Giorgio e il drago è un dipinto a olio su tela (57×73 cm) di Paolo Uccello, conservato alla National Gallery di Londra e databile al 1460 circa. Sebbene notoriamente l'uso della tela come supporto per i dipinti sia divenuto popolare a Venezia verso la fine del Quattrocento, pare che i primi esempi di pittura su tela siano fiorentini. Questo dipint...

Halaman ini berisi artikel tentang aktris Amerika. Untuk perenang Olimpiade Australia, lihat Rachel Harris. Untuk orang dengan nama yang mirip, lihat Rachel Harris (disambiguasi). Rachael HarrisHarris di WonderCon 2017LahirRachael Elaine Harris12 Januari 1968 (umur 56)Worthington, Ohio, ASNama lainRachel HarrisAlmamaterOtterbein UniversityPekerjaanAktris, pelawakTahun aktif1992–sekarangSuami/istriAdam Paul (m. 2003; c. 2008)...





















