John Pennington Harman
|
Read other articles:

Muhammad IISultan GranadaBerkuasa22 Januari 1273 – 8 April 1302PendahuluMuhammad IPenerusMuhammad IIIInformasi pribadiKelahiranc. 1235Kematian8 April (umur 66–67)GranadaWangsaBanu NashriAyahMuhammad IIbuAisyah[1]AnakMuhammad III, Nashr, FathimahAgamaIslam Muhammad II (Arab: محمد الثانيcode: ar is deprecated ; juga dikenal dengan julukannya al-Faqih, yang berarti sang ahli agama, c. 1235 – 8 April 1302; berkuasa sejak tahun 1273 hingga kematiannya) adalah pe...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أغسطس 2019) سجن الدلفين الأسود (بالروسية: Чёрный дельфин) البلد روسيا الإمبراطورية الروسية الاتحاد السوفيتي تاريخ التأسيس 1773 الإحداثيات 51°09′20″N 54°59′35″E...

Pour les articles homonymes, voir Jurassic Park (homonymie). Cet article concerne le roman de Michael Crichton. Pour la série de films, voir Jurassic Park (série de films). Pour les autres significations, voir Jurassic Park (homonymie). Jurassic Park Crâne du tyrannosaure 5027 qu'est allé voir Tim avec sa famille au Muséum américain d'histoire naturelle Auteur Michael Crichton Pays États-Unis Genre Techno-thrillerScience-fiction Version originale Langue Anglais américain Titre Ju...

ThailandJulukanช้างศึก (Changsuek) (Gajah Perang)AsosiasiAsosiasi Sepak Bola ThailandKonfederasiAFC (Asia)Sub-konfederasiAFF (Asia Tenggara)PelatihMasatada IshiiPenampilan terbanyakKiatisuk Senamuang (134)Pencetak gol terbanyakKiatisuk Senamuang (71)Stadion kandangStadion RajamangalaKode FIFATHAPeringkat FIFATerkini 101 12 (15 Februari 2024)[1]Tertinggi43 (September 1998)Terendah165 (Oktober 2014)Peringkat EloTerkini 105 3 (19 Januari 2024)[2] Warna pertama Warna...

Jeff BezosBezos pada Januari 2018LahirJeffrey Preston Jorgensen12 Januari 1964 (umur 60)Albuquerque, New Mexico, USAAlmamaterUniversitas PrincetonPekerjaanPengusaha teknologiinvestorfilantropisTahun aktif1987–sekarangDikenal atasMendirikan Amazon dan Blue OriginKekayaan bersih US$196.5 Miliar (Oktober 2021)[1]GelarKetua, CEO, dan Presiden AmazonSuami/istriMacKenzie Bezos (m. 1993)Anak4 Jeffrey Preston Bezos (/ˈbeɪzoʊs/;[a...

Fictional character Fictional character Kyo KusanagiThe King of Fighters characterKyo Kusanagi in his original design by ShinkiroFirst gameThe King of Fighters '94 (1994)Created byYuichiro Hiraki, Shinichi Morioka[1]Portrayed bySean Faris (2010 film)Yuichi Nakamura (KOF All Star promo trailer)Voiced byJapaneseMasahiro Nonaka (KOF '94 - Neo Geo Heroes: Ultimate Shooting)[2]Tomoaki Maeno (KOF XIV - onwards)[3]Ryōtarō Okiayu (CD Drama)[4] Tomokazu Sugita (Japane...

For related races, see 1894 United States gubernatorial elections. 1894 Colorado gubernatorial election ← 1892 November 6, 1894 1896 → Nominee Albert McIntire Davis Hanson Waite Charles S. Thomas Party Republican Populist Democratic Popular vote 93,502 73,894 8,337 Percentage 51.95% 41.06% 4.63% County results McIntire: 40–50% 50–60% 60–70% ...

Seorang nenek. Seorang nenek yang sedang menyanyi Nenek adalah masing-masing ibu dari orang tua seseorang.[1] Setiap orang memiliki dua orang nenek kandung. Seseorang dapat disebut sebagai nenek jika anaknya telah memiliki anak, atau dengan kata lain ia telah memiliki cucu. Panggilan nenek merupakan panggilan dari seorang cucu yang ditujukan kepada ibu dari ayahnya maupun dari ibunya. Selain itu, secara tradisi, dalam sebagian besar bahasa dan kebudayaan setiap perempuan tua dapat dip...

21st episode of the 1st season of The Secret Circle PromThe Secret Circle episodeCassie (Britt Robertson) and Diana (Shelley Hennig) time travel to find the last crystalEpisode no.Season 1Episode 21Directed byAlex ZakrzewskiWritten byHolly HendersonDon WhiteheadProduction code2J6271Original air dateMay 3, 2012 (2012-05-03)Guest appearances Joe Lando Tim Phillipps Andrea Brooks Elise Gatien Chad Willett Sammi Rotibi Episode chronology ← PreviousTraitor Next →F...

Resort and casino in Las Vegas, Nevada, US Aria Resort and CasinoAria Resort and Casino seen from aboveShow map of Las Vegas StripShow map of Nevada Location Paradise, Nevada, United States Address 3730 South Las Vegas BoulevardOpening dateDecember 16, 2009; 14 years ago (2009-12-16)No. of rooms4,004Total gaming space150,000 sq ft (14,000 m2)Permanent showsViva Elvis (2010–2012)Zarkana (2012–2016)Notable restaurantsJean-Georges Steakhouse, Julian Serrano T...

Partai Komunis Chili Partido Comunista de ChileKetua umumGuillermo TeillierSekretaris JenderalLautaro Carmona [es]Kepala DeputiCamila VallejoDibentuk4 Juni 1912; 111 tahun lalu (1912-06-04)Kantor pusatVicuña Mackenna 31SantiagoSurat kabarEl SigloSayap pemudaPemuda Komunis ChiliKoalisiUnity for ChangeKeanggotaan (2017)52.356[1]IdeologiKomunismeMarxisme–LeninismePosisi politikSayap kiri[2]Afiliasi nasional Full list Konvensi Revolusioner (1912–1921) G...

Pertemuan sinode nasional di Dordrecht Pasal-Pasal Ajaran Dordrecht (atau juga dikenal sebagai Kanon Dordrecht atau hanya Pasal-Pasal Dordrecht, bahasa Inggris: Canons of Dort, Belanda: Dordtse Leerregelscode: nl is deprecated ) disusun dalam Sinode Dordrecht, sebuah pertemuan nasional gereja Reformed pada tahun 1618 dan 1619 di Dordrecht, Belanda yang juga dihadiri oleh perwakilan gereja-gereja Reformed dari berbagai negara. Pasal-Pasal Dordrecht merupakan sanggahan terhadap 'Lima Artike...

Pour les articles homonymes, voir Smog (homonymie). Smog à New York en 1978. Vues de Pékin un jour après la pluie (à gauche) et un jour ensoleillé avec le smog (à droite). Smog à Kuala Lumpur en 2005. Le smog[1], fumard[1] ou brumée[1] est un brouillard grisâtre urbain qui limite la visibilité dans l’atmosphère. Issu du mélange de particules fines et d'ozone, le smog est associé à plusieurs effets néfastes pour la santé et pour l'environnement. Étymologie Le terme smog est...

Pour les articles homonymes, voir Collection. Le collectionnisme accompagne le développement des arts de la civilisation occidentale.Honoré Daumier, Le Collectionneur de gravures (1857-1860), huile sur toile, Petit Palais. Une collection est à la fois un regroupement d'objets correspondant à un thème, et l'activité qui consiste à réunir, entretenir et gérer ce regroupement. La collection peut être pratiquée dans le cadre d'un loisir par un collectionneur qui constitue et stocke un...

Fourth Rahman cabinet4th Cabinet of MalaysiaPeople and organisationsHead of stateTuanku Ismail Nasiruddin Shah (1969–1970) Tuanku Abdul Halim (1970)Head of governmentTunku Abdul RahmanDeputy head of governmentAbdul Razak HusseinMember parties Alliance Party United Malays National Organisation Malaysian Chinese Association Parti Bumiputera Sarawak Malaysian Indian Congress Sarawak Chinese Association Status in legislatureCoalition government74 / 144Opposition partiesDemocratic Action PartyU...
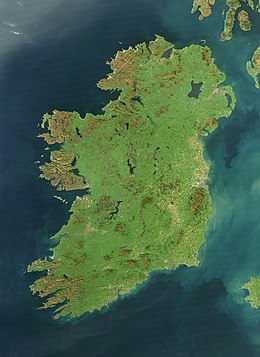
Geography of the island of Ireland, northwestern Europe Geography of IrelandContinentEuropeRegionNorthwestern EuropeArea • Total84,421 km2 (32,595 sq mi) • Land98.2% • Water1.8%Coastline7,524 km (4,675 mi)Highest pointCarrauntoohil 1,039 metres (3,409 ft)Lowest pointNorth Slob −3 metres (−10 ft)Longest riverRiver Shannon 360.5 km (224.0 mi)Largest lakeLough Neagh 392 km2 (151 sq mi)Climatetempe...

Organic reaction Shapiro reaction Named after Robert H. Shapiro Reaction type Coupling reaction Identifiers Organic Chemistry Portal shapiro-reaction RSC ontology ID RXNO:0000125 The Shapiro reaction or tosylhydrazone decomposition is an organic reaction in which a ketone or aldehyde is converted to an alkene through an intermediate hydrazone in the presence of 2 equivalents of organolithium reagent.[1][2][3] The reaction was discovered by Robert H. Shapiro in 1967. ...

Laurette TaylorLaurette Taylor pada sekitar tahun 1918LahirLoretta Helen Cooney(1883-04-01)1 April 1883New York City, New York, ASMeninggal7 Desember 1946(1946-12-07) (umur 63)New York City, New York, ASPekerjaanAktrisTahun aktif1912–1946Suami/istriCharles A. Taylor (m. invalid year; bercerai 1910) J. Hartley Manners (m. 1912; kematiannya 1928)AnakDwight Oliver Taylor Marguerit...
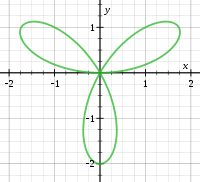
Point on a curve not given by a smooth embedding of a parameter In geometry, a singular point on a curve is one where the curve is not given by a smooth embedding of a parameter. The precise definition of a singular point depends on the type of curve being studied. Algebraic curves in the plane Algebraic curves in the plane may be defined as the set of points (x, y) satisfying an equation of the form f ( x , y ) = 0 , {\displaystyle f(x,y)=0,} where f is a polynomial function f : R 2 →...

مجوهراتمعلومات عامةصنف فرعي من فنون مرئيةفنون تطبيقيةزي وطني سُمِّي باسم حلية المنتجات حليةزينةfashion product (en) يمارسها صائغ ذهبمصمم مجوهراتcourt jeweler (en) رمز مهنة في تصنيف ISCO-88 الدولي الموحد للمهن 7313 تعديل - تعديل مصدري - تعديل ويكي بيانات خاتم من الألماس المعلقات الكهرمانية الم�...