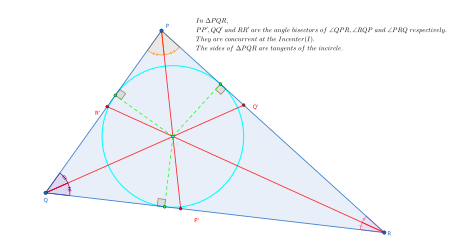
Incenter
|
Read other articles:

Pendar hayati yang dihasilkan jamur Panellus Stipticus. Jamur mengeluarkan cahaya hijau di malam hari untuk menarik serangga dalam membantu menyebarkan spora jamur. Ikon flora Taman Nasional Gunung Halimun Salak di Jawa Barat ini dikenal masyarakat setempat dengan sebutan “Supa Lumar”. Bioluminesensi atau pendar hayati[1] adalah emisi cahaya yang dihasilkan oleh makhluk hidup karena adanya reaksi kimia tertentu.[2] Hingga saat ini, bioluminesensi telah ditemukan secara ala...

لمعانٍ أخرى، طالع كورنينغ (توضيح). كورنينغ الإحداثيات 39°55′34″N 122°10′50″W / 39.926111111111°N 122.18055555556°W / 39.926111111111; -122.18055555556 تاريخ التأسيس 6 أغسطس 1907 تقسيم إداري البلد الولايات المتحدة[1][2] التقسيم الأعلى مقاطعة تيهاما خصائص جغرافية...

Le Maine, partagé en Bas-Maine à l'ouest, et Haut-Maine à l'est. Le Bas-Maine est la partie occidentale de l'ancienne province du Maine. La région est communément assimilée au département de la Mayenne, tout du moins à ses trois quarts nord, la frange sud du département faisant historiquement partie de l'Anjou. Le nom de Bas-Maine a été donné à une unité paysagère contemporaine par la Direction régionale de l'Environnement, de l'Aménagement et du Logement des Pays de la Loire...

Peta Azerbaijan yang menunjukan rayon Yardimli. Alam di Rayon Yardımlı Air terjun di Rayon Yardımlı Yardymli (Yardımlı) adalah sebuah rayon di Azerbaijan. Ibu kota rayon ini berada di Kota Yardmymli. lbsPembagian administratif Azerbaijan Distrik Absheron Agdam Agdash Aghjabadi Agstafa Agsu Astara Babek Balakan Barda Beylagan Bilasuvar Dashkasan Fuzuli Gadabay Goranboy Goychay Goygol Hajigabul Imishli Ismayilli Jabrayil Jalilabad Julfa Kalbajar Kangarli Khachmaz Khizi Khojaly Khojavend K...

French figure skater, surgeon, and politician Alain CalmatAlain Calmat at the 1964 World ChampionshipsBorn (1940-08-31) 31 August 1940 (age 83)Paris, FranceFigure skating careerCountryFranceRetired1965 Medal record Representing France Men's figure skating Olympic Games 1964 Innsbruck Men's singles World Championships 1965 Colorado Springs Men's singles 1964 Dortmund Men's singles 1963 Cortina d'Ampezzo Men's singles 1962 Prague Men's singles 1960 Vancouver Men's singles European Ch...

Constituency of the National Assembly of Pakistan NA-229 Karachi Malir-IConstituencyfor the National Assembly of PakistanRegionGadap Town (partly), Ibrahim Hyderi Town (partly), Shah Mureed, Bin Qasim Town and Murad Memon Town of Malir District in KarachiElectorate232,437 [1]Current constituencyMember(s)VacantCreated fromNA-258 Karachi-XX NA-229 Karachi Malir-I (این اے-229، کراچی ملیر-1) is a constituency for the National Assembly of Pakistan.[2] Members of Parl...

Scholastique MukasongaBiographieNaissance 20 décembre 1956 (67 ans)Province de Gikongoro (Ruanda-Urundi)Nationalités rwandaisefrançaiseActivité ÉcrivaineAutres informationsSite web scholastiquemukasonga.net/frDistinctions Liste détailléePrix Renaudot (2012)Prix Ahmadou-Kourouma (2012)Prix Simone-de-Beauvoir pour la liberté des femmes (2021)Chevalier des Arts et des LettresŒuvres principales Notre-Dame du Nil, La femme au pieds nus (d)modifier - modifier le code - modifier Wikida...

Peta Romania dengan wilayah Transylvania yang ditandai dengan warna kuning. Transilvania (juga Ardeal; bahasa Hongaria: Erdély; bahasa Jerman: Siebenbürgenⓘ; bahasa Bulgaria: Трансилвания; bahasa Serbia: Трансилванија / Transilvanija atau Ердељ / Erdelj; bahasa Latin: Transsilvania) adalah wilayah historis di Romania tengah dan barat. Pada awal sejarah, teritori Transilvania masuk ke dalam wilayah Dacia, kekaisaran Romawi, kekaisaran Hun, kera...

2022 anime television series Legend of Mana: The Teardrop CrystalKey visual聖剣伝説 —THE TEARDROP CRYSTAL—(Seiken Densetsu: The Teardrop Crystal)Created bySquare Enix Anime television seriesDirected byMasato JinboWritten byMasato JinboMusic byYoko ShimomuraStudioYokohama Animation LaboratoryGraphinicaLicensed byCrunchyroll SEA: Muse CommunicationOriginal networkMBS, TBSOriginal run October 8, 2022 – December 24, 2022Episodes12 (List of episodes) Legend of Ma...

Sinotrans&CSC GroupCompany typeState-owned enterpriseIndustryShipping and LogisticsFounded2008HeadquartersBeijing, People's Republic of ChinaArea servedWorldKey peopleExecutive Director and President: Song Dexing[1]Revenue89.044 billion renminbi (2015)[2]Number of employees51,511 (2015)[2]Websitewww.sinotrans-csc.com Sinotrans Changhang, or Sinotrans&CSC Holdings, is the largest logistics company of the People's Republic of China, with further interests in ship...

2000 television filmThis article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Up, Up and Away film – news · newspapers · books · scholar · JSTOR (May 2019) (Learn how and when to remove this message) Up, Up and AwayFilm posterGenreFantasyComedyWritten byDaniel BerendsenDirected byRobert TownsendStarringRobert Tow...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Würzburg Fortress Marienberg dengan Old Main Bridge di bagiand depan Lambang kebesaranLetak Würzburg NegaraJermanNegara bagianBayernWilayahLower FranconiaKreisDistrik perkotaanPemerintahan • MayorGeorg Rosenthal (SPD)Luas • Total87,63 km2 (3,383 sq mi)Ketinggian177 m (581 ft)Populasi (2013-12-31)[1] • Total124.698 • Kepadatan14/km2 (37/sq mi)Zona waktuWET/WMPET (UTC+1/+2)Kode pos97018–97084Kode area...

Genus of flowering plants Barbeya Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Clade: Rosids Order: Rosales Family: BarbeyaceaeRendle[1] Genus: BarbeyaSchweinf. ex Penzig Species: B. oleoides Binomial name Barbeya oleoidesSchweinf. Barbeya is the only genus in the family Barbeyaceae, and has only one species, Barbeya oleoides. It is a small tree native to the mountains of Somalia, Ethiopia, and the Arabian Peninsula. It can be...

Pour les articles homonymes, voir Gravity. Gravity Données clés Réalisation Alfonso Cuarón Scénario Alfonso CuarónJonás CuarónRodrigo García Musique Steven Price Acteurs principaux Sandra BullockGeorge Clooney Sociétés de production Esperanto FilmojReality MediaWarner Bros.Heyday Films Pays de production États-Unis Royaume-Uni Genre Action, drame, science-fiction, catastrophe, thriller Durée 91 minutes Sortie 2013 Pour plus de détails, voir Fiche technique et Distribution. modi...

Town in Region Nordjylland, DenmarkStøvringTownStøvring churchStøvringLocation in DenmarkShow map of DenmarkStøvringStøvring (North Jutland Region)Show map of North Jutland RegionCoordinates: 56°53′12″N 9°49′43″E / 56.88667°N 9.82861°E / 56.88667; 9.82861Country DenmarkRegionRegion NordjyllandMunicipalityRebildFoundationAround 17th centuryArea • Urban6.2 km2 (2.4 sq mi)Population (2024)[1] • Urba...

Virtuix OmniImage of Virtuix Omni.InventorJan GoetgelukManufacturerVirtuix Inc.Current supplierenterprise.virtuix.com/commercial-inquiries/Websitewww.virtuix.comNotesReleased January 2017 The Virtuix Omni is an omnidirectional treadmill simulator for virtual reality games and other applications. It uses a platform to simulate locomotion i.e. the motion of walking, requiring both special shoes or shoe covers and a surface that reduces friction. It works in conjunction with the HTC Vive, and a...

Overview of and topical guide to war The following outline is provided as an overview of and topical guide to war: War – organised and often prolonged armed conflict that is carried out by states or non-state actors – is characterised by extreme violence, social disruption, and economic destruction.[1][2] War should be understood as an actual, intentional and widespread armed conflict between political communities, and therefore is defined as a form of political violence o...

Airport in Paraná, Argentina General Justo José de Urquiza AirportAeropuerto de Entre Ríos General Justo José de UrquizaIATA: PRAICAO: SAAPSummaryAirport typePublic / MilitaryOperatorAeropuertos Argentina 2000LocationParaná, ArgentinaElevation AMSL243 ft / 74 mCoordinates31°47′40″S 60°28′49″W / 31.79444°S 60.48028°W / -31.79444; -60.48028MapPRALocation of airport in ArgentinaRunways Direction Length Surface m ft 02/20 2,100 6,890 Asphalt...

Place of burial For other uses, see Cemetery (disambiguation). Graveyard and Burial ground redirect here. For other uses, see Graveyard (disambiguation) and Burial Ground (disambiguation).Resting place redirects here. For the 1986 TV series, see Resting Place. For the 1951 film, see No Resting Place. Not to be confused with Rest area.This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages) This article pos...