Fundamental solution
|
Read other articles:

Institut Ilmu Kesehatan Bhakti WiyataIIK Bhakta : Institut Kesehatan Pertama di Indonesia[1]Nama sebelumnyaPendidikan Bhakti Husada 1985MotoDeveloping Health ExpertsMoto dalam bahasa IndonesiaMengembangkan Ahli KesehatanMoto dalam bahasa InggrisDeveloping Health ExpertsDidirikan2005 (2005)[2]PendiriDr. Bambang Harsono Suhartono, MBA.AfiliasiYayasan Bhakti WiyataAfiliasi akademikKemenristek Dikti RI, Kemenkes RIAkreditasiBRektorProf. Dr. Muhamad Zainuddin, A...

VAZ-2101InformasiProdusenVAZ, sekarang AvtoVAZJuga disebutLada 1200/1200SLada 1300Lada 2101 [1]VAZ-2101Masa produksi1970–1988PerakitanTolyatti, Uni SovietBodi & rangkaKelasMobil kompakBentuk kerangka4-pintu sedan5-pintu estateTata letakFront-engine, rear-wheel-driveMobil terkaitFiat 124SEAT 124Tofaş Murat 124Premier 118NEVAZ-2103VAZ-2106VAZ-2107Penyalur dayaMesinBensin:1.2 L VAZ-2101 I41.3 L VAZ-21011 I41.5 L VAZ-2103 I4Transmisi4-percepatan Manual3-per...

NGM-81 Jenis Senapan serbu Negara asal Hungaria Sejarah pemakaian Digunakan oleh Hungaria Spesifikasi Peluru 5,45 x 39 mm5,56 x 45 mm Mekanisme Operasi gas Amunisi Magazen box 30 butir NGM atau NGM-81 adalah senapan serbu buatan Hungaria hasil adposi dari AK-74 dan menggunakan peluru 5,45 x 39 mm. Varian ekspor dari senapan ini menggunakan peluru 5,56 x 45 mm.[1] Selain popor tetap senapan ini dibuat juga dengan popor besi lipat dengan nama NGV.[2] Catatan kak...

Marcello Leppe Informasi pribadiNama lengkap Marcello Romeo LeppeTanggal lahir 11 April 1948 (umur 75)Tempat lahir Viareggio, ItaliaPosisi bermain GelandangInformasi klubKlub saat ini Guangzhou Evergrande (pelatih)Karier junior1963–1969 Stella Rossa ViareggioKarier senior*Tahun Tim Tampil (Gol)1969 Sampdoria 0 (0)1969–1970 Savona 21 (2)1970–1978 Sampdoria 274 (5)1979–1982 Pistoiese 59 (1)Total 354 (8)Tim nasional‡ Italia U-23 2 (0)Kepelatihan1982–1985 Sampdoria (tim muda)198...

Algerian footballer Adlène Guedioura Guedioura with Algeria in 2012Personal informationFull name Adlène Guedioura Pons[1]Date of birth (1985-11-12) 12 November 1985 (age 38)Place of birth La Roche-sur-Yon, FranceHeight 1.78 m (5 ft 10 in)[2]Position(s) MidfielderTeam informationCurrent team CR BelouizdadNumber 25Youth career1992–2004 Racing ParisSenior career*Years Team Apps (Gls)2004–2005 Sedan 0 (0)2005–2006 Noisy-le-Sec 15 (1)2006–2007 L'Entent...

Charles Stuart Kaufman (lahir 1 November 1958) adalah seorang penulis skenario ternama dari Amerika Serikat. Film-filmnya mempunyai kecenderungan skenario yang unik, tidak bisa ditebak, biasanya berkarakter-ganda (seseorang berpikir tentang dirinya sendiri, melihat dirinya sendiri di kehidupan lain), dan berimaginasi liar. Awal kariernya dimulai dengan menulis skenario di televisi. Dia menjadi perhatian ketika skenarionya untuk Being John Malkovich, mendapat nominasi Penghargaan Oscar dan BAF...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Iltja Ntjarra Many Hands Art Centre – news · newspapers · books · scholar · JSTOR (April 2020) (Learn how and when to remove this template message) The t...

This article is about a radio station. For the Seattle station formerly known as KRAB, see KSER. For other uses, see Krab (disambiguation). Radio station in Greenacres, CaliforniaKRABGreenacres, CaliforniaBroadcast areaBakersfield metropolitan areaFrequency106.1 MHz (HD Radio)BrandingALT 106.1: KRAB RadioProgrammingFormatAlternative rockAffiliationsCompass Media NetworksPremiere NetworksOwnershipOwneriHeartMedia, Inc.(iHM Licenses, LLC)Sister stationsKBFP, KBFP-FM, KDFO, KHTYHistoryFirst air ...

Mosque in Baku, Azerbaijan Baba Kuhi Bakuvi mosqueAzerbaijani: Baba Kuhi Bakuvi məscidiReligionAffiliationIslamLocationLocation Old City, BakuCountryAzerbaijanLocation within AzerbaijanGeographic coordinates40°21′57.956″N 49°50′13.236″E / 40.36609889°N 49.83701000°E / 40.36609889; 49.83701000ArchitectureStyleIslamic architectureCompleted9th century Baba Kuhi Bakuvi mosque (Azerbaijani: Baba Kuhi Bakuvi məscidi) is one of the oldest mosques in Baku, the ca...

Online music distribution company Ditto MusicCompany typePrivateIndustryMusicGenreOnline distribution, Record labelFounded2005FounderLee Parsons, Matt ParsonsHeadquartersLiverpool, United KingdomArea servedWorldwideKey peopleLee ParsonsMatt ParsonsProductsRecord Label Services, Online Delivery (Music)ServicesRecord Label Services and On-demand music distributionNumber of employees103WebsiteDitto Music Website Ditto Music is an online music distribution company. It distributes music to 160 dig...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Sang SekretarisSutradaraNayato Fio NualaProduserSys NSDitulis olehAviv ElhamPemeranRico VeraldAngel KaramoyNikita MirzaniPutra DinataPenata musikBanuPerusahaanproduksiMitra PicturesSSS PicturesTanggal rilis22 September 2016Durasi80 menitNegara IndonesiaBahasaIndonesia Sang Sekretaris merupakan film drama Indonesia yang dirilis pada 22 September 2016. Film ini dibintangi oleh Angel Karamoy, Nikita Mirzani, dan Rico Verald. Disutradarai oleh Nayato Fio Nuala. Sinopsis Reno (Rico Vera...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

Santo AnsgarSanto AnsgariusSanto AnsgariusLahir(801-09-08)8 September 801AmiensMeninggal3 Februari 865(865-02-03) (umur 63)BremenDihormati diGereja Ortodoks Timur, Katolik Roma, Gereja Lutheran, Gereja AnglikanPesta3 FebruariPelindungDenmark Santo Ansgar atau Ansgarius (Corbie, *796? or 8 September? 801 – 3 Februari 865*, di Bremen), juga disebut Anskar atau Oscar , adalah Kepala Uskup Hamburg-Bremen. Ia dikanonisasi oleh Paus Nikolas I.[1] Santo Ansgarius adalah Uskup Agung da...
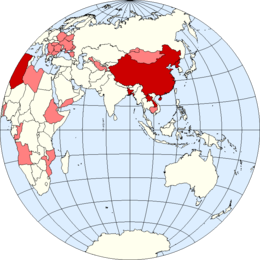
Карта государств, использующих название «народная республика»: Современные народные республики Бывшие народные республики Народная республика или народно-демократическая — официальное название, обычно используемое некоторыми нынешними или бывшими коммуни�...

Men's association football team representing Wales This article is about the men's senior team. For the women's senior team, see Wales women's national football team. WalesNickname(s)The Dragons (Welsh: Y Dreigiau)AssociationFootball Association of Wales (FAW)ConfederationUEFA (Europe)Head coachRob PageCaptainAaron RamseyMost capsGareth Bale (111)Top scorerGareth Bale (41)Home stadiumCardiff City StadiumFIFA codeWAL First colours Second colours FIFA rankingCurrent 29 (4 April 2024)[1]...

Biological process to convert light into chemical energy Schematic of photosynthesis in plants. The carbohydrates produced are stored in or used by the plant. Composite image showing the global distribution of photosynthesis, including both oceanic phytoplankton and terrestrial vegetation. Dark red and blue-green indicate regions of high photosynthetic activity in the ocean and on land, respectively. Photosynthesis (/ˌfoʊtəˈsɪnθəsɪs/ FOH-tə-SINTH-ə-sis)[1] is a system of bio...

He Changgong Chinese general He Changgong (Chinese: 何长工; January 27, 1901 – December 29, 1987) was a Chinese male politician, who served as the vice chairperson of the Chinese People's Political Consultative Conference. [1][2] References ^ 何虎生, 李耀东, 向常福主编 (2003). 中华人民共和国职官志. 北京: 中国社会出版社. ISBN 9787800883934.{{cite book}}: CS1 maint: multiple names: authors list (link) ^ 历届全国政协委员人名�...

Questa voce sull'argomento informatica è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Macworld Conference & ExpoIngresso del Macworld Expo 2007. LuogoMoscone Center, San Francisco Anni1985 - 2014 FrequenzaAnnuale DateGennaio GenereMondo Apple OrganizzazioneMacworld Modifica dati su Wikidata · Manuale Il Macworld Conference & Expo, inizialmente anche Macworld Exposition e negli ultimi ann...

72nd annual meeting of National Football League franchises to select newly eligible players 2007 NFL draftGeneral informationDate(s)April 28–29, 2007TimeNoon EDT (April 28)11:00 am EDT (April 29)LocationRadio City Music Hallin New York City, NYNetwork(s)ESPN, ESPN2, NFL NetworkOverview255 total selections in 7 roundsLeagueNFLFirst selectionJaMarcus Russell, QBOakland RaidersMr. IrrelevantRamzee Robinson, CBDetroit LionsMost selections (11)Atlanta FalconsGreen Bay PackersJacks...
















![{\displaystyle [-\Delta ]\Phi (\mathbf {x} ,\mathbf {x} ')=\delta (\mathbf {x} -\mathbf {x} ')}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dfed9de89c800b1f67eac39c7017337d7a03774)

![{\displaystyle [-\Delta +k^{2}]\Phi (\mathbf {x} ,\mathbf {x} ')=\delta (\mathbf {x} -\mathbf {x} '),\quad k\in \mathbb {R} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5aa8bc93820f8de79891d9e03916124face126c3)


![{\displaystyle [-\Delta ^{2}]\Phi (\mathbf {x} ,\mathbf {x} ')=\delta (\mathbf {x} -\mathbf {x} ')}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2ddfb4c64d0556a94e8b4b6eaf8b474853c3ef0)
