Circuit complexity
|
Read other articles:

Star in the constellation Camelopardalis 11 Camelopardalis A light curve for BV Camelopardalis, plotted from Hipparcos data[1] Observation dataEpoch J2000.0 Equinox J2000.0 Constellation Camelopardalis Right ascension 05h 06m 08.45273s[2] Declination +58° 58′ 20.5432″[2] Apparent magnitude (V) 5.08[3] Characteristics Spectral type B3 Ve[4] B−V color index −0.080[5&...

Tomasz Welna Datos personalesNacimiento Ciechanów, Polonia27 de enero de 1993 (30 años)Nacionalidad(es) Altura 1.87 metrosCarrera deportivaDeporte FútbolClub profesionalDebut deportivo 2011(Dolcan Ząbki)Club Polonia VarsoviaPolonia PoloniaLiga II Liga de PoloniaPosición Defensor[editar datos en Wikidata] Tomasz Welna (Ciechanów, Polonia, 27 de enero de 1993) es un futbolista polaco. Juega de defensor y su equipo actual es el Polonia Varsovia de la I Liga de Polonia. ...

Este artigo ou seção pode conter informações desatualizadas. Se tem conhecimento sobre o tema abordado, edite a página e inclua as informações mais recentes, citando fontes fiáveis e independentes. —Encontre fontes: ABW • CAPES • Google (N • L • A) Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências. Conteúdo não verificável pode ser removido.—Encontre fontes: ABW R...

احتفال جورج دبليو بوش أثناء التوقيع على قانون سياسة الطاقة لعام 2005 الذي قدم حوافز لبناء مفاعل نووي أمريكي بما في ذلك دعم تجاوز التكاليف بما يصل إلى ملياري دولار لستة محطات نووية جديدة.[1][2] بناء اثنين من المفاعلات في عام 2011 منAP1000 النهضة النووية في الولايات المتحدة ب�...

Technological college in New York, U.S. National Technical Institute for the DeafTypePrivate-Public partnershipEstablished1965PresidentGerard BuckleyLocationHenrietta, New York43°05′14″N 77°40′06″W / 43.0871°N 77.6683°W / 43.0871; -77.6683Websiterit.edu/ntid The National Technical Institute for the Deaf (NTID) is the first and largest technological college in the world for students who are deaf or hard of hearing.[1] As one of nine colleges within t...

Public college in Mahwah, New Jersey, US Ramapo College of New Jersey (RCNJ)TypePublic liberal arts collegeEstablished1969; 54 years ago (1969)Academic affiliationsSea-grant, Space-grantEndowment$21.2 million (2020)[1]PresidentCindy JebbStudents5,732[2]Undergraduates5,145Postgraduates587LocationMahwah, New Jersey, U.S.CampusSuburban, 300 acres (120 ha)Colors Maroon & whiteSporting affiliationsNCAA Division IIIMascotRoadrunnerWebsitewww.r...

Egyptian writer Youssef RakhaNative nameيوسف رخاBorn (1976-06-12) June 12, 1976 (age 47)Cairo, EgyptLanguageEnglish, ArabicAlma materUniversity of Hull (BA)SubjectCairo; Islam; the Arab SpringYears active1999–presentNotable worksThe Book of the Sultan's SealSpouseHeba El Nahhas (m. 2011)Websitetherakha.net Literature portal Youssef Rakha (Arabic: يوسف رخا; born on 12 June 1976 in Cairo, Egypt) is an Egyptian writer. His work explores language and identi...

List of autoracing series circuts The following is a list of circuits that have hosted International Motor Sports Association (IMSA) SportsCar Championship races from the inaugural season in 1971 up to and including the 2023 season. The list includes the combined IMSA history of races held as part of the IMSA GT Championship, the Grand-Am Rolex Sports Car Series, the American Le Mans Series and the current WeatherTech SportsCar Championship.[1][2] Several nations have hosted a...

Iago Informações pessoais Nome completo Iago Amaral Borduchi Data de nascimento 23 de março de 1997 (26 anos) Local de nascimento Monte Azul Paulista, São Paulo, Brasil Nacionalidade brasileiro Altura 1,81 m Pé canhoto Informações profissionais Clube atual Augsburg Número 22 Posição lateral-esquerdo Clubes de juventude 2011–20122013–2016 Atlético Monte AzulInternacional Clubes profissionais2 Anos Clubes Jogos e gol(o)s 2017–20192019– InternacionalAugsburg 0081 000...
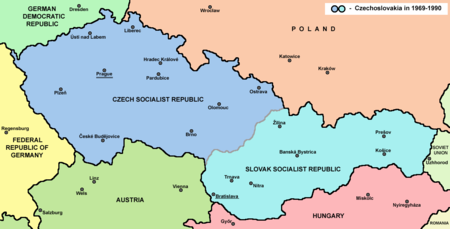
تفكك تشيكوسلوفاكيا (بالتشيكية: Zánik Československa) بالسلوفاكية: Rozdelenie Česko-Slovenska) بدأ هذا الحدث بتاريخ 1 يناير 1993 بتقسيم دولة تشيكوسلوفاكيا الفيدرالية إلى التشيك وسلوفاكيا.[1] قادت الثورة المخملية في عام 1989 لإنهاء حكم الحزب الشيوعي التشيكوسلوفاكي وت...

Pour les articles homonymes, voir Royaume d'Italie. Cet article présente la liste des Rois d'Italie de 787 à 1946 et les actuels prétendants. Roi d'ItalieRe d'Italia Armoiries royales d'Italie Dernier roi d'ItalieHumbert II(1946) Création 15 avril 787 (premier roi d'Italie) Abrogation 13 juin 1946 Premier titulaire Pépin Ier (roi d'Italie) Dernier titulaire Humbert II (roi d'Italie) modifier Historique Le concept de royaume d'Italie renvoie à des réalités historiques différente...

Indian politician (1927 - 1994) M. BasavarajuMember of Karnataka Legislative AssemblyIn office1967–1972Member of Rajya SabhaIn office3 April 1980 – 2 April 1986 Personal detailsBorn(1927-11-01)1 November 1927Died10 May 1994(1994-05-10) (aged 66)Political partyIndian National CongressSpouseShrimati ChikkananjammanniChildren4 sons and 2 daughters.ParentHasan Muddanna (father) M. Basavaraju ( 1 November 1927 - 10 May 1994) was an Indian politician of the Indian National Congres...

1985 San Marino Grand PrixRace detailsRace 12 of 12 races in the1985 Grand Prix motorcycle racing seasonDate1 September 1985Official nameGrand Prix San Marino[1]LocationCircuito Internazionale Santa MonicaCoursePermanent racing facility3.488 km (2.167 mi)500 ccPole positionRider Eddie LawsonTime 1:19.630Fastest lapRider Eddie LawsonTime 1:20.460PodiumFirst Eddie LawsonSecond Wayne GardnerThird Randy Mamola250 ccPole positionRider Carlos LavadoTime 1:22.550Fastest...

Historic district in North Carolina, United States United States historic placeHayes Barton Historic DistrictU.S. National Register of Historic PlacesU.S. Historic district Vance Street neighborhoodShow map of North CarolinaShow map of the United StatesLocationRoughly bounded by St. Mary's St., Fairview Rd., W. Roanoke Park Dr., Scales St. and Williamson Dr., Raleigh, North CarolinaCoordinates35°48′14″N 78°38′57″W / 35.80389°N 78.64917°W / 35.80389; -78.649...

BPRS Bhakti SumekarLogo BPRS Bhakti SumekarJenisBank Pembiayaan Rakyat SyariahIndustriPerbankanDidirikan16 September 2002KantorpusatSumenep, IndonesiaWilayah operasiSumenep dan PamekasanProdukTabungan Deposito Gadai emasPemilikPemkab SumenepSitus webhttp://bhaktisumekar.co.id/ BPRS Bhakti Sumekar (dahulu bernama BPR Bhakti Sumekar) adalah sebuah Badan Usaha Milik Daerah (BUMD) Kabupaten Sumenep. Bank ini didirikan pada tanggal 16 September 2002 dengan bentuk perseroan terbatas (PT), kemudian ...

Pour les articles homonymes, voir Cantal. CantalPays d’origine FranceRégion Auvergne, Cantal, Auvergne-Rhône-AlpesPâte pressée non cuite, pressée (en)Appellation Appellation d'origine contrôlée (1956)appellation d'origine protégéeNommé en référence à Monts du CantalVolume commercialisé 13 186 t (2017)Aire de production 1 000 000 ha (2005)modifier - modifier le code - modifier Wikidata Le cantal (ou fourme de cantal) est un fromage français à pâte pressée non...

This X-ray film reveals a poor crown-to-root ratio for tooth #21 (right), the lower left first premolar. The tooth exhibits 50% bone loss, adding roughly 5-7 mm to the clinical crown of what is actually anatomical root. The fulcrum, existing somewhere immediately apical to the height of the bone, does not allow for any adjacent bone to avoid compression or tension, resulting in virtually complete widening of the PDL and a grim prognosis, due to secondary occlusal trauma. Crown-to-root-ratio i...

Serbian officer and military writer You can help expand this article with text translated from the corresponding article in Serbian. (February 2022) Click [show] for important translation instructions. View a machine-translated version of the Serbian article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-...

Gustavo de Arístegui Embajador de España en la India 15 de abril de 2012-13 de diciembre de 2015 Diputado en las Cortes Generalespor Guipúzcoa, Ciudad Real y Zamora 27 de marzo de 2000-13 de diciembre de 2011 Información personalNombre en inglés Gustavo De Aristegui Nacimiento 6 de junio de 1963 (60 años)Madrid, EspañaNacionalidad EspañolaFamiliaPadre Pedro Manuel de Arístegui y Petit Información profesionalOcupación AbogadoPartido político Partido PopularSitio web gustavodea...

Assembly constituency in Maharashtra Sindkhed Raja Assembly constituency is one of the 288 constituencies of the Maharashtra Vidhan Sabha and one of the seven which are located in the Buldhana district. Sindkhed RajaConstituency No. 24 for the Maharashtra Legislative AssemblyConstituency detailsCountryIndiaRegionWestern IndiaStateMaharashtraDistrictBuldhanaLS constituencyBuldhanaReservationNoneMember of Legislative Assembly14th Maharashtra Legislative AssemblyIncumbent Dr. Shingne Rajendra Bh...




































